1. Определитель. Порядок определителя. Свойства определителей (доказательство свойств).
2. Минор. Алгебраическое дополнение.
3. Разложение определителя по строке и столбцу.
4. Матрицы. Классификация матриц.
5. Линейные операции на матрицах, их свойства.
6. Транспонирование матриц.
7. Произведение матриц.
8. Элементарные преобразования на матрицах.
9. Обратная матрица, ее свойства. Необходимое и достаточное условие существования обратной матрицы.
10. Ранг матрицы. Метод нулей и единиц нахождения ранга матрицы.
11. Совместность системы линейных алгебраических уравнений. Теорема Кронекера-Капелли.
12. Матричный метод решения системы линейных алгебраических уравнений.
13. Метод Гаусса решения системы линейных алгебраических уравнений.
14. Векторы. Классификация векторов. Линейные операции над векторами, их свойства.
15. Линейная зависимость и независимость векторов. Базис.
16. Декартова система координат.
17. Радиус-вектор точки. Координаты точки. Координаты вектора.
18. Направляющие косинусы вектора.
19. Длина вектора в координатах.
20. Деление отрезка в заданном отношении.
21. Проекция вектора на ось, ее свойства.
22. Скалярное произведение векторов, его свойства.
23. Физический смысл скалярного произведения векторов.
24. Выражение скалярного произведения векторов в координатной форме.
25. Векторное произведение векторов, его свойства.
26. Геометрический смысл векторного произведения векторов.
27. Физический смысл векторного произведения векторов.
28. Выражение векторного произведения векторов в координатной форме.
29. Смешанное произведение векторов, его свойства.
30. Геометрический смысл смешанного произведения векторов.
31. Выражение смешанного произведения векторов в координатной форме.
32. Общее уравнение прямой на плоскости.
33. Уравнение прямой на плоскости в отрезках.
34. Каноническое уравнение прямой на плоскости.
35. Уравнение прямой на плоскости, проходящей через две заданные точки.
36. Уравнение прямой на плоскости по точке и вектору нормали.
37. Уравнение прямой на плоскости с угловым коэффициентом.
38. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых на плоскости.
39. Плоскость. Общее уравнение плоскости.
40. Исследование уравнения плоскости.
41. Уравнение плоскости в отрезках.
42. Уравнение плоскости, проходящей через три заданные точки.
43. Уравнение плоскости по точке и вектору нормали.
44. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей.
45. Параметрические уравнения прямой в пространстве.
46. Канонические уравнения прямой в пространстве.
47. Уравнения прямой в пространстве, проходящей через две точки.
48. Общие уравнения прямой в пространстве.
49. Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности двух прямых в пространстве.
50. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
51. Кривые второго порядка: Окружность. Эллипс. Гипербола. Парабола.
52. Определения кривых второго порядка, канонические уравнения, построение линий.
Примерный вариант практических примеров для экзамена
1. Проверить совместность системы уравнений и в случае совместности решить ее:
а) с помощью обратной матрицы (матричным методом)
б) методом Гаусса.
а)  б)
б) 
2. Решить СЛАУ:  .
.
3. Решить СЛАУ:  .
.
4. Даны две матрицы  и
и  .
.
Найти: а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 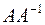 ; д)
; д)  ; е)
; е)  матрицы А;
матрицы А;
ж)  матрицы В.
матрицы В.
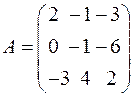 ,
,  .
.
5. Решить матричное уравнение:  .
.
6. Вычислить  - направляющий косинус вектора
- направляющий косинус вектора  , если
, если  и
и  .
.
7. Даны три точки А (-1; 0; 3), В (8; 2; -1), С(4; -2; 6).
Найти:
1) Проекцию вектора 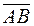 на вектор
на вектор  , т.е.
, т.е.  ;
;
2) Площадь r АВС;
3) Выяснить, будет ли вектор  ортогонален вектору
ортогонален вектору 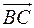 , если М - середина отрезка ВС.
, если М - середина отрезка ВС.
4) Проверить, образуют ли векторы  базис, и найти координаты вектора
базис, и найти координаты вектора  в этом базисе.
в этом базисе.
5) Правую или левую тройку образуют векторы  .
.
6) Вычислить  и
и  , если
, если  и
и  .
.
7) Перпендикулярны ли векторы 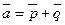 и
и  , если
, если  ,
,  ,
, 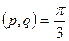 .
.
8. Найти  , если
, если  ,
,  и
и  .
.
9. Найти аппликату вектора (2k + 3j) × i.
10. При каком действительном  площадь треугольника с вершинами
площадь треугольника с вершинами 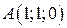 ,
, 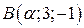 ,
,  равна
равна  ?
?
11. Дано: a = m – n, b = 2m + 3n, c = m – 2n, | m | = 1, | n | = 2, <(m, n) = 2π/3. Вычислить (a + b) · c.
12. Найти уравнение плоскости, параллельной плоскости 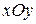 , расположено на расстоянии равном 5 от неё.
, расположено на расстоянии равном 5 от неё.
13. Написать уравнение плоскости, проходящей через точки А(3, -1, 2) и В(2,0, -1) перпендикулярно плоскости х-у+1=0.
14. Напишите уравнение прямой, проходящей через точку А(-1;2;3) параллельно прямой  .
.
15. Определить тип кривой  . Привести ее уравнение к каноническому виду. Сделать схематический чертеж.
. Привести ее уравнение к каноническому виду. Сделать схематический чертеж.
16. Построить линию у2 – 2у + х = 0.
Примерный вариант билета
1. Проекция вектора на ось. Составляющие вектора.
2. При каком значении m векторы  коллинеарны. Записать разложение вектора
коллинеарны. Записать разложение вектора  по составляющим.
по составляющим.
3. Исследовать систему на совместность. Решить систему уравнений 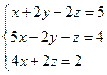 .
.
4. Силы  и
и  приложены к точке
приложены к точке  . Вычислить работу, совершаемую равнодействующей этих сил, когда ее точка приложения перемещается в положение
. Вычислить работу, совершаемую равнодействующей этих сил, когда ее точка приложения перемещается в положение  .
.
5.

Дано:

| Найти:

|
6.
 , найти обратную матрицу, если она существует, вычислить
, найти обратную матрицу, если она существует, вычислить  .
.
7. Найти длину диагоналей параллелограмма, построенного на векторах  ,
,  , если
, если 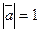 ,
,  ,
,  .
.
8. Вывести канонические уравнения прямой в пространстве.
9. Определение эллипса. Основа уравнения эллипса.
10. Найдите точку пересечения прямой  и плоскости 4х+у-6z-5=0.
и плоскости 4х+у-6z-5=0.
11. Построить область, ограниченную указанными линиями:  ;
;  ;
; 
12. Составить уравнение окружности, диаметром которой служит отрезок прямой 3х+4у-12=0, заключенный между осями координат.






