Анализ устойчивости оптимальных решений к изменению коэффициентов целевой функции

Анализ оптимальных решений в задачах ЛП

 

Необходимость анализа оптимальных решений

 

Получение оптимального решения в задачах линейного программирования не всегда означает завершение работ по обоснованию и выработке оптимальной стратегии поведения. В реальной экономике часто случается так, что изменения во внешней среде — колебания спроса, рост инфляции и т.д. — приводят, например, к необходимости корректировки цен на продукцию. Для оптимизационной модели это означает внесение корректив в целевую функцию. Тут же возникают вопросы: каким образом и к чему такие коррективы могут привести? Кроме того, обычно для реализации производственной программы существует возможность привлечения дополнительных финансовых и других ресурсов либо перераспределения уже имеющихся. Вполне естественно попытаться выяснить, к чему это приведет и как скажется на уже полученном оптимальном решении. Иначе говоря, после решения задачи оптимизации в силу разных причин могут возникнуть вполне закономерные вопросы.

1. Насколько устойчиво полученное оптимальное решение к изменению параметров модели, в частности коэффициентов целевой функции? Что произойдет, например, если спрос на продукцию упадет (возрастет) и, следовательно, придется снизить или повысить цену на то или иное изделие? Что в этом случае делать с полученной ранее оптимальной производственной программой? Потребуется ее корректировка или нет?

2. Насколько чувствительно полученное решение к изменениям запасов ресурсов, т. е. к изменению правых частей в неравенствах системы ограничений? Изменится ли доходность (значение целевой функции) при изменении запасов и насколько?

3. Как оценить вклад единицы каждого из ресурсов в доходность? Какие ресурсы целесообразно увеличить в первую очередь? К какому результату это может привести? Не являются ли запасы некоторых ресурсов избыточными и, вместо затрат на их приобретение и хранение, не лучше ли пополнить запасы тех ресурсов, которые в наибольшей степени увеличивают доходность и расходуются полностью? Как количественно просчитать (оценить) различные варианты «ресурсного» поведения?

Получение ответов на перечисленные вопросы и составляет существо анализа оптимальных решений.

Заметим, что в линейном программировании под устойчивостью обычно подразумевают неизменность оптимальных решений при изменениях (вариациях) коэффициентов целевой функции, а под чувствительностью — степень влияния правых частей ограничений на прирост, либо уменьшение значений целевой функции.

С точки зрения обоснования управленческих решений, анализ устойчивости и чувствительности часто играет не менее важную роль, чем отыскание собственно оптимального решения.

 

Анализ устойчивости оптимальных решений к изменению коэффициентов целевой функции

 

Выясним вначале, как влияет изменение коэффициентов целевой функции на оптимальное решение. Такая проблема возникает в случаях, когда, например, меняется рыночная ситуация, приводящая к колебаниям спроса и, следовательно, к изменению стоимости единицы продукции. Для иллюстрации рассмотрим задачу нахождения оптимальной производственной программы с двумя переменными. С точки зрения модели линейного программирования это приводит к необходимости изменения коэффициентов с₁,с₂ целевой функции (целевых коэффициентов).

Пусть для некоторой исходной целевой функции

Z₁ = c₁ x₁+ c₂ x₂

получено оптимальное решение (x_1opt, x_2opt). Выясним, изменится ли оно при изменении коэффициентов с₁,с₂. Для этого рассмотрим два случая:

Z₂ = c₁*x₁ + c₂*x₂ и Z₃ = c₁**x₁ + c₂**x₂

Заметим, что значение самой целевой функции Z всегда будет либо увеличиваться, либо уменьшаться при любом изменении с₁, с₂. Однако важнее выяснить другое: изменится ли при этом ранее найденное оптимальное решение (x_1opt, x_2opt) или нет.

Иначе говоря, требуется определить, достигается ли наибольшее значение новой целевой функции с измененными коэффициентами в той же точке (x_1opt, x_2opt), что и ранее, или оптимальное решение будет достигаться при другой комбинации переменных (х₁, х₂).

Как было показано в главе 3, коэффициенты целевой функции однозначно определяют вектор 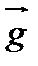, указывающий направление возрастания значений Z. Следовательно, трем рассматриваемым случаям будут соответствовать три разных направления роста целевых функций. Линии уровня (прямые, во всех точках которых Z = const) всегда перпендикулярны вектору g. Следовательно, ориентация линий уровня и направления возрастания Z для трех случаев будет различной (рис. 4.1).

X₂

X1

 

Рис. 4.1.

 

Сопоставим этот вывод с «поведением» линий уровня в ОДР.

Заметим, что область допустимых решений при изменении целевых коэффициентов остается неизменной. Пусть, например, ОДР задачи изображена на рис. 4.2 и пусть оптимальное решение для исходной задачи находится в точке А. Анализируя положение линий уровня для рассматриваемых целевых функций, устанавливаем (рис. 4.2) следующее.

 

A

X₂

X1

B

Z1

Z2

Z3

 

Рис. 4.2.

 

1. Для целевой функции Z₂ = c₁*x ₁ + c₂*x₂ точка оптимума не изменилась и по-прежнему находится в вершине А. Это означает, что максимальное значение целевой функции Z₂ = c₁*x ₁ + c₂*x₂ достигается в той же оптимальной точке, что и ранее (х_1A,х_2A).

2. Точка оптимума для целевой функции Z₃ = c₁**x₁ + c₂**x₂ переместилась в точку B (в другую вершину ОДР). Это означает, что теперь максимального значения целевой функции Z₃ можно добиться только при новой комбинации переменных (х_1B,х_2B).

 

Таким образом:

1. Изменение коэффициентов целевой функции в рамках некоторого диапазона не приводит к изменению оптимального решения (x_lopt, x_2opt). Такой диапазон называют диапазоном устойчивости решения по коэффициенту целевой функции.

2. Границы диапазона устойчивости зависят как от ОДР, так и от целевой функции.

3. При изменениях целевых коэффициентов, выходящих за границы диапазона устойчивости, оптимальное решение (x_1opt, x_2opt) меняется. Оно перемещается в другую точку ОДР.

При решении задач линейного программирования с большим числом переменных определение границ устойчивости, в принципе, не составляет труда, однако требует применения довольно громоздких вычислительных процедур. Вместе с тем эти алгоритмы легко реализуются на ЭВМ. Они включены во многие стандартные пакеты соответствующих программ линейной оптимизации, в том числе и в MS Excel. Все выводы, полученные для задачи с двумя переменными, справедливы и для задач со многими переменными.