Таблица №1.
| № Вари анта | Две последние цифры шифра | Номера задач | № Вари анта | Две последние цифры шифра | Номера задач |
| 01 51 | 1 32 41 11 | 26 76 | 6 38 48 20 | ||
| 02 52 | 2 33 42 12 | 27 77 | 7 39 49 11 | ||
| 03 53 | 3 34 43 13 | 28 78 | 8 40 50 12 | ||
| 04 54 | 4 35 44 14 | 29 79 | 9 31 42 14 | ||
| 05 55 | 5 36 45 15 | 30 80 | 1 34 44 15 | ||
| 06 56 | 6 37 46 16 | 31 81 | 2 35 45 16 | ||
| 07 57 | 7 38 47 17 | 32 82 | 3 36 46 17 | ||
| 08 58 | 8 39 48 18 | 33 83 | 4 37 47 18 | ||
| 09 59 | 9 40 49 19 | 34 84 | 5 38 49 19 | ||
| 10 60 | 10 31 50 20 | 35 85 | 6 39 48 20 | ||
| 11 61 | 1 31 42 21 | 36 86 | 7 40 41 10 | ||
| 12 62 | 2 32 43 22 | 37 87 | 8 31 50 11 | ||
| 13 63 | 3 33 44 23 | 38 88 | 9 32 42 22 | ||
| 14 64 | 4 34 45 24 | 39 89 | 10 33 43 13 | ||
| 15 65 | 5 35 46 25 | 40 90 | 1 35 45 14 | ||
| 16 66 | 6 36 47 26 | 41 91 | 2 36 46 15 | ||
| 17 67 | 7 37 48 27 | 42 92 | 3 37 47 16 | ||
| 18 68 | 8 38 49 29 | 43 93 | 4 38 48 17 | ||
| 19 69 | 9 39 50 30 | 44 94 | 5 39 49 18 | ||
| 20 70 | 10 40 41 21 | 45 95 | 6 40 50 19 | ||
| 21 71 | 1 33 43 10 | 46 96 | 7 31 41 20 | ||
| 22 72 | 2 34 44 22 | 47 97 | 8 32 42 11 | ||
| 23 73 | 3 35 45 1 5 | 48 98 | 9 33 43 15 | ||
| 24 74 | 4 36 46 18 | 49 99 | 10 32 44 16 | ||
| 25 75 | 5 37 47 19 | 50 100 | 10 31 41 17 |
Контрольная работа № 1.
Задача 1.
В цепи, схема которой приведена на рис. 1, амперметр показывает ток I3=1 А. Определить напряжение сети U, эквивалентное сопротивление Rэкв и мощность Р, потребляемую цепью, если R1=1 Ом, R2=3 Ом, R3=30 Ом, R4=7 Ом, R5=8 Ом.

|
Рис. 1
Задача 2.

|
Цепь постоянного тока, схема которой приведена на рис. 2 состоит из 4 резисторов, сопротивление которых равны: R1=20 Ом; R2=40 Ом; R3=30 Ом; R4=5 Ом. Ток в цепи I=2 А.Определить эквивалентное сопротивление цепи Rэкв, токи, проходящие через каждый резистор, I1, I2, I3 и мощность, потребляемую цепью Р.
Рис. 2
Задача 3.
В цени, схема которой приведена на рис 3, амперметр показывает ток I4-5=0.5 А, вольтметр показывает напряжение U4 =4 В.
Определить напряжение сети U, ток I1в первом резисторе и мощность Р, потребляемую цепью, если R1=25 0м, R2=20 Ом, R5=12 Ом, R3=5 Om.

Рис. 3
Задача 4.
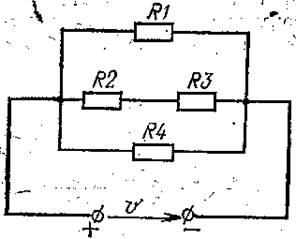
Цепь постоянного тока, схема которой приведена на рис. 4, состоит из 4 резисторов, сопротивление которых равны: R1=12 Ом, R2=2 Ом, R3=4 Ом, R4=4 Ом. Мощность всей цепи Р=50 Вт.
Определить эквивалентное сопротивление цепи Rэкв, напряжение и токи, проходящие через каждый резистор, I1, I2, I3, I4.
|
Рис. 4
Задача 5.

|
В цепи, схема которой приведена на рис. 5, амперметр показывает ток I2 =0.5 А. Определить напряжение сети U и мощность Р, потребляемую цепью, если R1=6 Ом, R2=60 Ом, R3=20 Ом, R4 =10 Ом, R5 =40 Ом.
Рис. 5
Задача 6.
Цепь постоянного тока, схема которой приведена на
рис. 6, состоит из 4 резисторов, сопротивления которых равны: R1=5 Ом, R2=6 Ом, R3=12 Ом, R4=6 Ом, напряжение, приложенное к цепи, U=60 В.

|
Определить эквивалентное сопротивление всей цепиRэкв; мощность, потребляемую цепью, Р и токи, проходящие через каждый резистор: I1, I2, I3, I4
Рис. 6
Задача 7
В цепи, схема которой приведена на рис. 7, амперметр показывает ток I4 = 1А, вольтметр напряжение U5 = 12 В.

|
Определить, эквивалентное сопротивление цепи R экв, напряжение сети U, мощность, потребляемую цепью, Р, если
R1 = 15 Ом, R2=30 Ом, R3=10 Ом, R5=12 Ом.
Рис. 7
Задача 8.
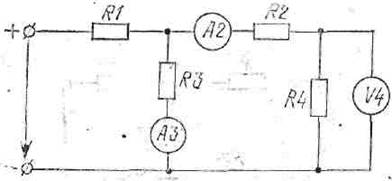
Определить эквивалентное сопротивление цепи, схема которой представлена на рис. 8, а также показания амперметров А2, A3 и вольтметра V4, если напряжение сети U=40 В, R1=20 Ом, R2=60 Ом, R3=40 Ом, R4=40 Ом.
|
Рис. 8
Задача 9.
Цепь постоянного тока, схема которой приведена на рис. 9 состоит из 4 резисторов, сопротивления которых равны; R1=3 Ом; R2=10 Om; R3=30 Ом; R4=20 Ом; общий ток в цепи I=3 А.

|
Определить эквивалентное сопротивление цепи R экв, напряжение, приложенное к цепи, и токи, проходящие через каждый резистор.
Рис. 9
Задача 10
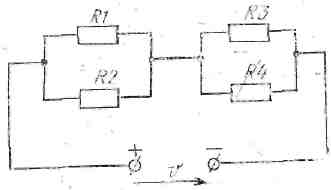
Цепь постоянного тока, схема которой приведена рис. 10, состоит из 4 резисторов, сопротивления которых равна R1=60 Ом; R2=30 Ом; R3=30 Ом; R4=20 Ом. Мощность всей цепи Р=288 Вт.
|
Определить эквивалентное сопротивление цепи Rэкв, напряжение на каждом резисторе U1; U2, U3, U4.
Рис. 10
В равномерном магнитном поле индукцией В=1 Тл перпендикулярно к линиям поля со скоростью v=l2,5м/с перемещается проводник длиной l=24 см (рис. 11). К проводнику присоединен потребитель, сопротивление которого R=0,55 Ом.
Определить электромагнитную силу, действующую на

|
проводник, если сопротивление самого проводника R0=0.5 Ом.
Рис. 11
Задача 12
По прямолинейному проводнику, расположенному в вакууме, проходит ток I=50 А. Одна из магнитных линий этого поля с радиусом а =0.05 м. относительно оси проводника показана на рис. 12.
Определить числовые значения напряженности магнитного поля Н и магнитной индукции В в точке А. Перечертить рисунок и показать на нём направление вектора напряженности магнитного поля Н в указанной точке.

|
Рис. 12
Задача 13.
Проводник длиной l=20 см. находится в магнитном поле с индукцией В =1.25 Тл. И присоединён к зажимам сети, напряжение которой U=5 В. (рис. 13). Сопротивление проводника R=0.3 Ом Вследствие взаимодействия тока с магнитным полем, проводник движется со скоростью v=8 м/с перпендикулярно направлению вектора индукции.

|
Определить ток в проводнике и действующую на него электромагнитную силу.
Рис. 13
Задача 14.
|
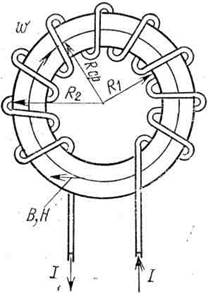
Определить напряженность и магнитную индукцию по средней линии кольцевой катушки, если радиус Rcp=12 см и число витков ω=1200; по катушке проходит ток I= 25 А. Сердечник выполнен из неферромагнитного материала (рис. 14).
Рис. 14
Задача 15.
Определить подъемную силу F электромагнита, изображенного на рис. 15, если, площадь сечения полюса S = 12*10ˉ4 м2, а магнитная индукции В = 0,7 Тл.

|
Рис. 15
Задача 16.
Цилиндрическая катушка (рис. 16) с немагнитным сердечником (относительная магнитная проницаемость μ=l), у которой длина l=0,25 м. значительно больше диаметра d=0,05 м, имеет обмотку с числом витков ω=3000, распределенную равномерно по длине сердечника. По обмотке катушки проходит ток I=5 А, создавая вокруг неё магнитный поток Ф.
Определить значение магнитного потока Ф и индуктивность катушки L.

|
Рис. 16
Задача 17
По проводнику длиной l=2 м, находящемуся в однородном магнитном поле с индукцией В = 0,8 Тл и расположенному в плоскости, перпендикулярной направлению поля, проходит ток I от источника питания с напряжением U=5 В.На проводник действует электромагнитная сила Fэм, перемещающая его со скоростью v = 2,5 м/с. Сопротивление проводника с подводящими проводами R=1 Ом.
Определить значение тока I в неподвижном проводнике, противоЭДС, индуцированную в проводнике, и ток I в движущемся проводнике. Исходные данные по рис. 13.
Задача 18.
Узкая кольцевая катушка, изображенная на рис. 17, имеетразмеры: R1=0,l4 м; 'R2=0,13 м, при которых(R1 - R2)<R1; число витков ω=400, равномерно распределенных вдоль немагнитного сердечника (относительная магнитная проницаемость μ=l). Поверхность, ограниченная окружностью радиуса R, совпадающего со средней магнитной линией пронизывается полным током ΣI=Iω, где I=0,15 А.
Определить напряженность магнитного поля Н и магнитную индукцию В на средней магнитной линии.

|
Рис. 17
Задача 19.
Прямолинейный провод с током расположен в однородном магнитном поле в плоскости S (рис. 18), перпендикулярной линиям магнитной индукции поля В=1 Тл. Под действием электромагнитной силы Fэм провод переместился на расстояние b=0.25 м. Длина провода l=0.4 м.; ток в проводе I=160 А.
Определить электромагнитную силу Fэм и механическую работу, совершенную этой силой при перемещении провода.

|
Рис. 18
Задача 20.
Определить индуктивность цилиндрической катушки без сердечника, если она имеет длину 1 =12 см, радиус витка R=4 см, а число витков ω=2200.
Определить величину ЭДС самоиндукции, если ток в катушке увеличивается со Скоростью 200 А/с.

|
Рис. 19
Задача 21.
В сопротивлении, точная величина которого R=8,5 Ом, проходит Ток I=14 А. При измерении напряжения на этом
сопротивлении вольтметр показал напряжение U=121 В.
Определить абсолютную и относительную погрешности этого измерения. Начертить электрическую схему цепи.
Задача 22.
Амперметр, включенный в цепь нагрузки, рассчитан на номинальный ток Iн=5 А., снабжен шунтом, сопротивление которого Rш=0,02 Ом. Сопротивление измерительного механизма Rn=10 Ом.
Определить ток In и напряжение Un измерительного механизма, а также шунтовой множитель n. Начертить схему включения измерительного механизма с шунтом.
Задача 23.
Измерительный механизм магнитоэлектрической системы спряжением UH=75 мВ с внутренним сопротивлением Rн=10 Ом необходимо использовать для измерения напряжения Uн=l20 В.
Найти величину добавочного сопротивления, которое нужно включить последовательно с измерительным механизмом, и ток в вольтметре. Начертить схему включении измерительного механизма с добавочным сопротивлением.
Задача 24.
Измерительный механизм магнитоэлектрической системы
рассчитай на ток IH=l5 мА, внутреннее сопротивление прибора Rn=10 Ом.
Определить сопротивление шунта и добавочное сопротивление для измерения этим прибором тока Iн=6 А. и напряжения Uн=30 В. Начертить схемы включения измерительного механизма: а) с шунтом и б) с добавочным сопротивлением.
Задача 25.
В однофазную цепь переменного тока с активно-индуктивной нагрузкой включены амперметр, вольтметр и ваттметр. Показания приборов: амперметра—4 А., вольтметра—127 В., ваттметра — 400 Вт.
Определить полное и активное сопротивления и коэффициент мощности цепи. Начертить схему соединений, указать системы применяемых приборов.
Задача 26.
При проверке технического вольтметра, имеющего предел измерения (номинальное напряжение) UH==150 В и класс точности γд=1%, была определена его наибольшая абсолютная погрешность ΔUнаиб=1,8 В.
Определить приведенную погрешность прибора γп и сделать вывод о соответствии вольтметра указанному на нем классу точности.
Задача 27.
Однофазный потребитель подключен к сети с напряжением U =620 В. Активная мощность потребителя Р=440 Вт при токе I=2,5 А.
Определить коэффициент мощности установки cos φ и энергию W, израсходованную за 30 часов работы.
Начертить схему соединений с приборами для измерения U, I, P и указать системы применяемых приборов.
Задача 28.
Миллиамперметр с пределом измерения (номинальным током) 1н = 250 мА имеет класс точности γд=1.5%.
Определить наибольшую абсолютную погрешность миллиамперметра ΔIнаиб и наибольшую возможную относительную погрешность γн.в. при измерении этим прибором только I=200 мА.
Задача 29.
Ваттметр, включенный для измерения активной мощности
однофазного потребителя, имеет следующие номинальные
данные: Uн=300 В; Iн=1 А, число делений шкалы, αн=150.
При измерении стрелка ваттметра отклонилась на α=100 делений.
Определить показание ваттметра Р и электрическую энергию W, которая израсходована потребителем за t=22 часа работы.
Задача 30.
В сеть переменного тока напряжением V=220 В. включина катушка, индуктивность которой L=25.4 мГн и активное сопротивление R=6 Ом. Частота сети f=50 Гц.
Определить ток I в катушке; активную Р, реактивную Q и полную S мощности; угол сдвига фаз между током и.напряжением. Начертить электрическую схему цепи. Построить в масштабе векторную диаграмму напряжений и пояснить ее построение.
Задача 31.
В сеть переменного тока напряжением V=220 В. включина катушка, индуктивность которой L=25.4 мГн и активное сопротивление R=6 Ом. Частота сети f=50 Гц.
Определить ток I в катушке; активную Р, реактивную Q и полную S мощности; угол сдвига фаз между током и.напряжением. Начертить электрическую схему цепи. Построить в масштабе векторную диаграмму напряжений и пояснить ее построение.
Задача 32.
Для неразветвленной цепи переменного тока (рис. 20) с активным R1=6 Ом и индуктивным XL1=8 Ом, сопротивлениями задана мощность цепи Р=54 Вт.

|
Определить полное сопротивление цепи и ток цепи I, U−напряжение, приложенное к цепи; реактивную Q и полную S мощности цепи. Построить в масштабе векторную диаграмму напряжений и пояснить её построение.
Рис. 20
Задача 33.
Для неразветвленной цепи переменного тока (рис. 21) с активным R1=10 Ом, R2=6 Ом и индуктивными XL1=8 Ом, XL2=4 Ом сопротивлениями задано напряжение приложенное к цепи, U=80 В.
Определить полное сопротивление цепи z, токи цепи I, активную Р, реактивную Q и полную S мощности цепи. Построить в масштабе векторную диаграмму напряжений и пояснить её построение.

|
Рис. 21
Задача 34. '
Для неразветвленной цепи переменного тока (рис. 22) с активным R1=40 Ом и емкостным XC1=30 Ом сопротивлениями задан ток I=4 А.

|
Определить полное сопротивление цепи z, напряжение, приложенное к цепи, U, угол сдвига фаз между током и напряжением, активную Р, реактивную Q и полную S мощности цепи. Построить в масштабе векторную диаграмму напряжений и пояснить ее построение.
Рис. 22
Задача 35.
Для неразветвленной цепи переменного тока (рис. 23) с активным R1=80 Ом, индуктивным XL1=100 Ом, емкостным Xc1=40 Ом сопротивлениями задано напряжение, приложенное к цепи U=200 В.
Определить полное сопротивление цепи z; ток цепи I; активную Р, реактивную Q и полную S мощности цепи; угол сдвига фаз между током и напряжением. Построить в масштабе векторную диаграмму напряжений пояснить её построение.

|
Рис. 23
Задача 36.
В сеть переменного тока напряжением U=50 В (рис. 24) включены параллельно катушка, параметры которой R1=16 Ом и XL1= 12 Ом и батарея конденсаторов, емкостное сопротивление которой Xс2=24 Ом.
Определить токи в параллельных ветвях I1, I2 и ток в неразветвленной части цепи I. Построить в масштабе векторную диаграмму токов и пояснить её посроение.

|
Рис. 24
Задача 37.
В сеть переменного тока напряжением U=420 В. включены параллельно конденсатор и реостат с активным сопротивлением R1=12 Ом. Ток в конденсаторе I2=6 А.
Определить ток в реостате I1; ток в неразветвлённой части цепи I; активную Р, реактивную Q и полную Sмощности, потребляемые цепью. Начертить электрическую схему цепи. Построить в масштабе векторную диаграмму токов и пояснить её построение.
Задача 38.
Цепь переменного тока содержит активные сопротивления R1=32 Ом; R2=24 Ом и ёмкостные Xс1=24 Ом; XС2=32 Ом, образующие две параллельные ветви (рис. 25). Ток во второй ветви I2=2 А.
Определить ток в первой ветви I1; ток I в неразветвлённой части цепи; напряжение U, приложенное к цепи; активную Р, реактивную Q и полную S мощности, потребляемые всей цепью. Построить в масштабе векторную диаграмму токов и пояснить её построение.

|
Рис. 25
Задача 39.
Цепь переменного тока содержит индуктивное XL1=10 Ом и ёмкостное XC2=20 Ом сопротивления, образующие две параллельные ветви (рис. 26). Напряжение, приложенное к цепи U=100 В.

|
Определить токи в обеих параллельных ветвях I1, I2, а также ток I в неразветвлённой части цепи; активную Р, реактивную Q и полную S мощности, потребляемые всей цепью. Построить в масштабе векторную диаграмму токов и пояснить её построение.
Рис. 26
Задача 40
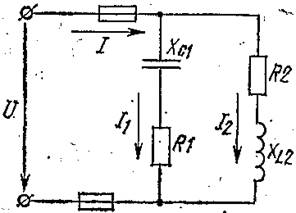
Цепь переменного тока содержит активные R1=12 Ом, R2=20 Ом и индуктивное XL2=15 Ом; ёмкостное RC1=16 Ом сопротивления, образующие две параллельные ветви (рис.27).
Определить токи в параллельных ветвях I1и I2, а также ток I в неразветвлённой части цепи; активную Р, реактивную Q и полную S мощности, потребляемой всей цепью. Построить в масштабе векторную диаграмму токов и пояснить её построение.
|
Рис. 27
Задача 41.
В четырехпроводную сеть трехфазного тока с линейным напряжением Uл=380 В. включены по схеме «звезда» лампы одинаковой мощности Рламп=200 Вт. Число ламп в фазах nA=10; nв=20; nс=15.
Вычислить активную мощность, потребляемую цепью; фазные напряжения и токи. Начертить электрическую схему цепи. Построить векторную диаграмму напряжений и токов; построение диаграммы пояснить. Определить по векторной диаграмме ток в нулевом проводе I0.
Задача 42.
В трехфазную сеть с линейным напряжением Uл=380 В, звездой включен приёмник энергии мощностью Р=6 кВт с коэффициентом мощности cos φ=0.85.
Начертить схему цепи. Определить фазное напряжение UФ; фазные токи IAB, Ibc, Iса и мощность Р, потребляемую всеми лампами. Построить в масштабе векторную диаграмму напряжении и токов; найти по векторной диаграмме значения токов в линейных проводах.
Задача 43.
В трехфазную сеть напряжением Uл=380 В включен двигатель. Обмотка двигателя соединена треугольником. Полное сопротивление каждой фазы обмотки двигателя zф=30 Ом; коэффициент мощности двигателя cos φ=0,84. Начертить схему цепи. Определить активную мощность двигателя Р; фазное напряжение Uф, фазный Iф и линейный Iл токи, активное Rф и индуктивное ХLф сопротивления фазы. Построить в масштабе векторную диаграмму напряжений и токов.
Задача 44.
В трехпроводную сеть трехфазного тока с линейным напряжением Uл=380 В включены по схеме «треугольник» лампы одинаковой мощности Рламп=150 Вт. Число ламп в фазах nАВ=12; nвс=18; nСА=24.
Вычислить фазные токи и активную мощность, потребляемую цепью. Начертить электрическую схему цепи. Построить векторную диаграмму напряжений и токов; построение диаграммы пояснить. Определить по векторной диаграмме линейные токи IA, Iв, Iс.
Задача 45.
В трехфазную сеть напряжением Uл=380 В звездой включен преемник энергии мощностью Р=6 кВт с коэффициентом мощности cos φ=0,85.
Начертить схему цепи. Определить фазное напряжение
Uф; фазный ток Iф и линейный, ток Iл; полное сопротивление
фазы zф; полную S и реактивную Q мощности трехфазного
потребителя. Построить в масштабе векторную диаграмму
напряжении и токов.
Задача 46.
В трёхфазную сеть с напряжением Uл=220 В включён двигатель, потребляющий мощность Р=9кВт. Обмотки двигателя соединены звездой. Линейный ток двигателя Iл=50 А.
Начертить схему цепи. Определить фазное напряжение Uф, полное zф, активное Rф и индуктивное XLф сопротивления фазы; коэффициент мощности cos φ, полную S и реактивную Q мощности двигателя. Построить в масштабе векторную диаграмму напряжений и токов.
Задача 47.
В четырёхпроводную сеть трёхфазного тока с линейным напряжением Uл=220 В включены лампы одинаковой мощности по схеме «звезда». Ток каждой лампы Iлампы= 0.79 А. Число ламп в фазах nA=12, nB=8, nC=15.
Вычислить мощность лампы; мощность, потребляемую цепью; фазные напряжения и токи. Начертить электрическую схему цепи. Построить векторную диаграмму напряжений и токов, построение диаграммы пояснить. Определить по векторной диаграмме ток в нулевом проводе.
Задача 48.
В трёхпроводную сеть трёхфазного тока с линейным напряжением Uл=220 В включены по схеме «треугольника» лампы одинаковой мощности Рламп=200 Вт. Мощности фаз РАВ=4 кВт, РВС=6 кВт, РСА8 кВт.
Определить число ламп в фазах, общую мощность потребителя, фазные токи. Начертить электрическую схему цепи. Построить векторную диаграмму напряжений и токов, построение диаграммы пояснить. Определить по векторной диаграмме линейные токи IA, IB, IC.
Задача 49.
В трёхфазную четырёхпроводную сеть с напряжением Uл=380 В. включены приёмник энергии по схеме «звезда». Мощность, приёмников в фазе А−РА=1.5 кВт, в фазе В−РВ=2 кВт, в фазе С−РС= 1 кВт. Для всех приёмников cos φ=1.
Начертить схему цепи. Определить фазные напряжения Uф; фазные Iф и линейные Iл токи; активную мощность трёх фаз. Построить в масштабе векторную диаграмму напряжений и токов; графический из векторной диаграммы определить ток в нулевом проводе I0.
Задача 50.
В четырёхпроводную сеть трехфазного тока включены по схеме «звезда» лампы одинаковой мощности. Ток одной лампы Iл=0,5 А; фазные токи IА=9 А; IB =4,5 A; IC =5,4 А. Фазные напряжения на лампах Uф=220 В.
Вычислить линейное напряжение сети, число ламп в фазах, общую мощность потребителя, мощность одной лампы. Начертит электрическую схему цепи. Построить векторную диаграмму напряжений и токов, построение диаграммы пояснить. Определить по векторной диаграмме ток в нулевом проводе I0.
Методические указания к выполнению
Контрольной работы № 1.
Задачи 1−10 включают материал темы 1.2 «Электрические цепи постоянного тока».
Для их решения необходимо знать закон Ома для всей цепи и участка, первый закон Кирхгофа, методику определения эквивалентного сопротивления цепи при смешанном соединении резисторов, а также уметь вычислить мощность электрического тока.
Методику и последовательность действий при решении задач 1−10 рассмотрим на конкретном примере.
Пример 1.

|
Определить эквивалентное сопротивление цепи Rэкв, схема которой представлена на рис. 28, если заданы значения сопротивлений резисторов R1=8 Ом, R2=4 Ом, R3=2 Ом, R4=4 Ом R5=4 Ом, Ом. Напряжение сети U=16 В. Вычислить токи, и мощность, потребляемую цепью.
Рис. 28
Решение.
1. Делаем краткую запись условия задачи.
Дано: R1=8 Ом, R2=4 Ом, R3=2 Ом, R4=4 Ом, R5=4 Ом; U=16 В.
Определить: Rэкв, I1, I2, I3, I4, I5, P.
2. Обозначим стрелками токи, проходящие через каждый резистор с учётом их направления, и узлы цепи буквами А, В, С, Д.
3.Определим общее эквивалентное сопротивление цепи, метод подсчёта которого для цепи со смешанным соединением резисторов сводится к последовательному упрощению схемы.
а) сопротивления R4 и R5 соединены параллельно, Найдём общее сопротивление при таком соединении:
R4,5=(R4 ∙ R5): (R4 + R5)=(4 ∙ 4): (4+4)=2 Ом.
б) теперь резисторы R2, R3, R4,5 соединены последовательно. Их общее сопротивление:
R2, 3, 4, 5= R2 + R3 + R4,5=4 + 2 + 2=8 Ом.
в) сопротивления R1 и R2, 3, 4, 5 соединены параллельно. Эквивалентное сопротивление цепи:
Rэкв=(R1 ∙ R2, 3, 4, 5): (R1 + R2, 3, 4, 5)=(8 ∙ 8): (8 + 8)=4 Ом.
4. Общий ток по закону Ома для участка цепи.
I=U: Rэкв=16: 4=4 А.
5. Токи, проходящие через сопротивление цепи.
а) ток в первом сопротивлении:
I1=U: R1=16: 8=2 А.
Сопротивление R1 соединено с зажимами цепи, поэтому напряжение на R1 равно: U1= U=16 В. Такое же напряжение на сопротивлении R2, 3, 4, 5.
б) ток во втором и третьем сопротивлениях:
I2=I3= I – I1=4 – 2=2 А.
в) чтобы найти токи I4 и I5, надо знать U4, 5. Это напряжение можно найти двумя способами:
U4, 5=I2 ∙ R4, 5 =2 ∙ 2=4 В,
U – (I2 ∙ R2) – (I3 ∙ R3)= U2 – (I2 ∙ R2) – (I3 ∙ R3)
или
U4, 5=U – U2 – U3=16 – 2 ∙ 4 – 2 ∙ 2=4 В.
По закону Ома для параллельно соединенных сопротивлении
I4=U4, 5: R4=4: 4=1 А;
I5=U4, 5: R5=4: 4=1 А;
Проверка
I2=I4 + I5.
2=1 + 1
2А=2А
6. Мощность, потребляемая цепью
P=U ∙ I=16 ∙ 4=64 Вт.
Задачи 31 – 40 посвящены расчету цепей однофазного переменного тока. При изучении материала темы 1.5 «Однофазные электрические цепи переменного тока» надо усвоить основные величины, характеризующие синусоидальные токи и напряжения: амплитуда, частота, начальная фаза, сдвиг фаз между током и напряжением, мгновенное и действующее значение. Надо научиться строить векторные диаграммы токов и напряжений сначала для цепи только с активным сопротивлением, только с индуктивным или только с ёмкостным сопротивлением, а затем для неразветвленной и разветвленной цепи, содержащей все три вида сопротивлений.
В неразветвленной (последовательной) цепи переменного тока приложенное напряжение определяется как геометрическая сумма активной и реактивной составляющих напряжения.
Для неразветвленной цепи строится векторная диаграмма напряжений и тока, причем за исходный вектор берется вектор тока, т.к. ток будет одинаковым во всех участках цепи.
Надо усвоить, что напряжение на активном сопротивлении совпадает с током по фазе, напряжение на индуктивности опережает ток на 90°, напряжение на ёмкости отстает от тока на 90°.
В разветвленной (параллельной) цепи общий ток, то есть ток в неразветвленном участке цепи, определяется как геометрическая сумма активной и реактивной составляющих тока. Сами параллельные ветви рассчитываются как неразветвленные цепи переменного тока. Для разветвленных цепей строится векторная диаграмма токов и напряжения, причем за исходный вектор берется вектор напряжения, т.к. на всех параллельных ветвях напряжение одинаковое.
Пример 7.
Активное сопротивление катушки Rк=4 Ом, индуктивное XL=12 Ом. Последовательно с катушкой включен резистор с активным сопротивлением R=2 Ом и конденсатор с сопротивлением XС=4 Ом. К цепи приложено напряжение U=100 В.
Определить полное сопротивление цепи, силу тока, коэффициент мощности, активную, реактивную и полную мощности; напряжение на каждом сопротивлении. Начертить в масштабе векторную диаграмму цепи. Схема цепи дана на рис. 33а.

|
Рис. 33а.
Решение.
1. Полное сопротивление цепи
 |
 z=√(Rк + R)² + (XL – XC)²=√(4 + 2)² + (12 – 4)²=10 Ом.
z=√(Rк + R)² + (XL – XC)²=√(4 + 2)² + (12 – 4)²=10 Ом.
2. Сила тока в цепи:
I=U: z=100: 10=10.
3. Коэффициент мощности цепи:
cosφ=(Rк + R): z=(4 + 2): 10=0,6.
По таблице Брадиса находим φ=53°10'.
4. Активная мощность цепи:
Р=I² ∙ (Rк + R)=10² ∙ (4 + 2)=600 Вт, или
Р=U ∙ I ∙ cosφ=100 ∙ 10 ∙ 0,6=600 Вт.
5. Реактивная мощность цепи:
Q=I² ∙ (XL – XC)=10² ∙ (12 – 4)=800 вар, или
Q=U ∙ I ∙ sinφ=100 ∙ 10 ∙ 0,8=800 вар, где
sinφ=(XL – XC): z=(12 – 4): 10=0,8.
6. Полная мощность цепи:


S=√P² + Q²=√600² + 800²=1000 В ∙ А.
7. Напряжение на сопротивлениях цепи:
Uк=I ∙ Rк=10 ∙ 4=40 В; UL=I ∙ XL=10 ∙ 12=120 B;
UR=I ∙ R=10 ∙ 2=20 B; UC=I ∙ XC=10 ∙ 4=40 B.
Построение векторной диаграммы начнем с выбора масштаба для тока и напряжения. Задаемся масштабом по току: МI=2,5 А/см и масштабом по напряжению: МU=20 В/см.
Построение векторной диаграммы (рис. 33б) начнем с вектора тока, длина которого откладывается по горизонтали в масштабе lI=I: MI=10 А: 2,5 А/см=4 см.
Вдоль вектора тока откладываем векторы напряжений на активных сопротивлениях Uk и UR, длины которых равны:
lUR=UR: МU=20 В: 20 В/см=1см;
lUK=Uk: МU=40 В: 20 В/см=2см.
Из конца вектора UR откладываем в сторону опережения вектора тока на 90° вектор напряжения UL на индуктивном сопротивлении длиной lU=UL: МU=120 В: 20 В/см=6 см.
Из конца вектора UL откладываем в сторону отставание от вектора тока на 90° вектор напряжения на конденсаторе UC длиной lUC=UC: МU=40 В: 20 В/см=2 см.

|
Геометрическая сумма векторов Uk, UR, UL и UC равна напряжению U, приложенному к цепи.
Рис. 33б.
Пример 8.
Катушка с активным сопротивлением R1=8 Ом и индуктивным XL1=6 Ом соединена параллельно с конденсатором, емкостное сопротивление которого равна XL2=20 Ом. (рис. 34а).

|
Определить: токи в ветвях и в неразветвленной части цепи, активные и реактивные мощности ветвей и всей цепи, полную мощность цепи, углы сдвиг фаз между током и напряжением в каждой ветви и во всей цепи. Начертить в масштабе векторную диаграмму цепи. К цепи приложено напряжение U=60 В.
Рис. 34а.
Решение.
1. Токи в каждой ветви:
 |  |
I1=U: z1; I2=U: z2, где z1=√ R1² + XL1²=√8² + 6²=10 Ом;
z2=XС2=20 Ом – полные сопротивления ветвей.
I1=60: 10=6 А; I2=60: 20=3 А.
2. Углы сдвиг фаз в ветвях находим по синусам углов во избежание потери знака угла:
sin φ1=XL1: z1=6: 10=0,6;
φ1=36°50', т.е. напряжение опережает ток, т.к. φ1>0;
sin φ2= –XС2: z2= –20: 20= –1;
φ2= –90°, т.е. напряжение отстает от тока, т.к. φ2<0.
По таблице Брадиса находим
cos φ1=cos 36°50'=0,8; cos φ2=0.
3. Активные и реактивные составляющие токов ветвей
Iа1= I1 cos φ1=6 ∙ 0,8=4,8 А; Iр1= I1 sin φ1=6 ∙ 0,6=3,6 А;
Iа2=0; Iр2=3 ∙ (–1,0)= –3 А.
4. Ток в неразветвленной части цепи:
 |  |
I=√(Iа1 + Iа2)² + (Iр1 + Iр2)²=√(4,8 + 0)² + (3,6 – 3)²=4,83 А.
5. Коэффициент мощности всей цепи:
cos φ=(Iа1 + Iа2): I=4,8: 4,83=0,992.
6. Активные и реактивные мощности ветвей и всей цепи:
Р1=I1² ∙ R1=6² ∙ 8=288 Вт; Р2=0
Р=Р1 + Р2=288 Вт.
Q1=QL=I1² ∙ XL1=6² ∙ 6=216 вар;
Q2=QС=I2² ∙ XС2=3² ∙ 20=180 вар;
Q= Q1 – Q2=216 – 180=36 вар.
Реактивная мощность ветвей с емкостью Q2 – Отрицательна, т.к. угол φ2<0.
7. Полная мощность цепи:

 S=√P² + Q²=√288² + 36²=296 В ∙ А.
S=√P² + Q²=√288² + 36²=296 В ∙ А.
Ток в неразветвленной части цепи можно определить и без разложения токов ветвей на составляющие:
I=S: U=296: 60=4,83 А.
8. Для построения векторной диаграммы задаемся масштабом по току: МI=1 А/см и масштабом по напряжению: МU=10 В/см. Построение начнем с вектора напряжения U (рис. 34б).
Под углом φ1 к нему (в сторону отставания) откладываем в масштабе вектор тока I1; под углом φ2 (в сторону опережения) – вектор тока I2. Геометрическая сумма этих токов равна току в неразветвленной части цепи. На диаграмме показаны также проекции векторов токов на вектор напряжения (активная составляющая Iа1) и вектор, перпендикулярный ему (реактивные составляющие Iр1 и Iр2).

|
Рис. 34б.
Задачи 41 – 50 посвящены теме 1.6 «Трехфазные электрические цепи». В трехфазных системах потребители соединяются по схеме «звезда» или «треугольник».
При соединении приемников энергии «звездой» линейные напряжения обозначаются UАВ, UВС, UАС, в общем виде – UЛ; фазные напряжения обозначаются UА, UВ, UС; в общем виде – UФ.
Токи – IА, IВ, IС; причем токи линейные равны соответствующим фазным токам:
IЛ= IФ.
При наличии нейтрального провода при любой нагрузке, а при равномерной нагрузке и без нейтрального провода:
UЛ=√3 ∙ UФ.
При соединении потребителей энергии «треугольником» фазное напряжение равно линейному UФ=UЛ. Обозначаются напряжения UАВ, UВС, UАС.
Фазные токи обозначаются IАВ, IВС, IАС, в общем виде IФ. Линейные токи обозначаются IА, IВ, IС, в общем виде IЛ. При неравномерной нагрузке фаз линейные токи определяются из векторной диаграммы, как геометрическая разность фазных токов.
При соединении приемников энергии звездой сеть может быть четырехпроводной – при наличии нейтрального провода, или трехпроводной – без нейтрального провода.  При соединении «треугольником» – только трехпроводной.
При соединении «треугольником» – только трехпроводной.
Пример 9.
Осветительные лампы трех этажей станции соединены «звездой» и присоединены к трехфазной четырехпроводной линии с линейным напряжением UЛ=380 В (рис. 35). Число ламп на каждом этаже одинаковое n1=n2=n3=50. Мощность каждой лампы Рламп=100 Вт.
Определить: фазные токи IА, IВ, IС при одновременном включении всех ламп на каждом этаже; фазные активные мощности РА, Рв, Рс и мощность Р всей трехфазной цепи; ответить на вопрос: чему будет равен ток в нейтральном проводе?

|
Рис. 35.
Решение.
1. Определить фазные мощности, исходя из того, что в каждой фазе включено по 50 ламп, Рламп=100 Вт каждая:
РА=РВ=РС=n1 ∙ Рламп=50 ∙100=5000 Вт=5 кВт.
Тогда мощность цепи Р=РА + РВ + РС=3 ∙ 5=15 кВт.
 2. Фазные (они же линейные) токи найдем их формулы фазной мощности РА=UФ ∙ IА ∙ cos φ, предварительно определив фазное напряжение UФ=UЛ: √3=380: 1,73=220 В; cos φА=cos φС=1 (нагрузка активная), тогда:
2. Фазные (они же линейные) токи найдем их формулы фазной мощности РА=UФ ∙ IА ∙ cos φ, предварительно определив фазное напряжение UФ=UЛ: √3=380: 1,73=220 В; cos φА=cos φС=1 (нагрузка активная), тогда:
IФ=IА=IВ=IС=РФ: (UФ ∙ cos φФ)=5000: (220 ∙1)=22,7 А.
3. Для определения тока в нейтральном проводе надо построить векторную диаграмму напряжений и токов. Выбираем масштаб МU=50 В/см, для токов МI=10 А/см. Длина векторов:
lUФ=UФ: МU=220: 50=4,4 см; lIА=lIВ=lIС=IФ: МI=22,7: 10=2,27 см;
Порядок построения диаграмм (Рис. 36).


 1. Из точки 0 проводим три вектора фазных напряжений UА, UВ, UС, углы между которыми составляют 120°.
1. Из точки 0 проводим три вектора фазных напряжений UА, UВ, UС, углы между которыми составляют 120°.


 2. Векторы фазных токов IА, IВ, IС будут иметь одинаковую длину, т.к. значение токов одинаковые. Направлены они вдоль соответствующих векторов фазных напряжений.
2. Векторы фазных токов IА, IВ, IС будут иметь одинаковую длину, т.к. значение токов одинаковые. Направлены они вдоль соответствующих векторов фазных напряжений.
3. Геометрически складываем токи IА, IВ, IС, получаем ток в нейтральном проводе I0;
 |  |  |  |
I0=IА + IВ + IС.
Из диаграммы (рис. 36) видно, что ток в нейтральном проводе I0 равен нулю.

|
Рис. 36.
Пример 10.
Трехфазный двигатель мощностью Р=15 кВт, при φ=0,87 питается от сети с линейным напряжением UЛ=380 В. Обмотки двигателя соединены треугольником (рис. 37).

|
Определим фазное напряжение UФ, фазный IФ и реактивную Q мощности двигателя. Построим в масштабе векторную диаграмму напряжений и токов.
Рис. 37.
Решение.
1. При соединении треугольником фазное напряжение равно линейному, т.е.:
UФ=UА=380 В.
2. Из формулы активной мощности находим фазный ток двигателя:
IФ=Р: (3 ∙ UФ ∙ cos φ)=15 ∙ 10³: (3 ∙ 380 ∙ 0,87)=15 А.
3. Полное сопротивление фазы по закону Ома:
zф=UФ: IФ=380: 15=25 Ом.
4. Линейный ток при равномерной нагрузке фаз:
 |  |
IЛ=√3 ∙ IФ=√3 ∙ 15=26 А.
5. Полная мощность двигателя:
S=3 ∙ UФ ∙ IФ=Р: cos φ=15000: 0,87=17240 В ∙ А ≈ 17,2 кВ ∙ А.
6. Реактивная мощность двигателя:
Q=3 ∙ UФ ∙ IФ ∙ sin φ=S ∙ sin φ=17240 ∙ 0,5=8620 вар≈8,6квар.






