При несовпадающих сопряженных поверхностях в месте соприкосновения двух тел при их силовом взаимодействии, когда площадка контакта относительно мала по сравнению с размерами тел, возникают местные напряжения смятия, которые называют контактными напряжениями. При этом радиусы кривизны тел в зоне контакта значительно больше размеров отпечатка, а начальное касание элементов происходит в точке или по линии в зависимости от формы контактирующих деталей. За расчетную величину контактных напряжений принимают максимальное давление в центре площадки контакта (при круговом или эллипсном отпечатке, рис 4.1, а и б), или продольной оси симметрии площадки контакта (при ленточной форме отпечатка, рис. 4.1, в).
а б в
Рис. 4.1. Поверхности контакта несовпадающих сопряжений
При решении контактной задачи Герцем был получен ряд зависимостей в предположении, что материалы соприкасающихся тел однородны и изотропные, площадки контакта весьма малы по сравнению с поверхностями соприкасающихся тел, действующие усилия направлены нормально к поверхности соприкосновения обоих тел, а нагрузки, приложенные к телам, создают в зоне контакта только упругие деформации, подчиняющиеся закону Гука.
В случае круговой площадки контакта можно применять следующие формулы:
контактное напряжение
; (4.7)
радиус площадки контакта
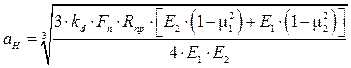; (4.8)
упругое сближение соприкасающихся тел
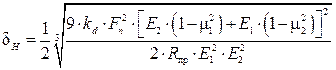. (4.9)
Здесь Fn – внешняя нормальная к поверхности контакта сила, Н;
kd – динамический коэффициент (для статической нагрузки kd =1, для динамической – kd =2);
E 1и Е 2 – модули нормальной упругости материалов соприкасающихся деталей, МПа;
µ1,2 – коэффициенты Пуассона материалов соприкасающихся деталей; R пр – приведенный радиус кривизны деталей в зоне контакта, мм.
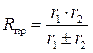, (4.10)
где r 1 и r 2 – радиусы контактирующих сфер (знак плюс – при внешнем контакте, знак минус – при внутреннем контакте), мм.
Если коэффициенты Пуассона материалов соприкасающихся деталей µ=0,3, то формулы (4.8-4.10) принимают вид:
; (4.11)
; (4.12)
, (4.13)
где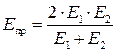 
(4.14)
– приведенный модуль нормальной упругости тел, МПа.
На практике часто встречаются более сложные случаи сопряжения деталей, например, контакт шарика с беговыми дорожками наружного и внутреннего колец шарикоподшипника (рис. 4.2).
Рис. 4.2. Схема контакта шарика шарикоподшипника с беговыми дорожками
Рассмотрим контакт шарика с беговой дорожкой внутреннего кольца. В плоскости, проходящей через центр шарика и ось подшипника, имеет место внутренний контакт сопряженных кривых, а приведенный радиус кривизны будет иметь большее значение:
. (4.15)
В плоскости, проходящей через центр шарика и перпендикулярной оси подшипника, имеет место внешний контакт сопряженных кривых, я приведенный радиус кривизны будет иметь меньшее значение:
. (4.16)
Для подобных сопряжений деталей при определении контактных напряжений можно использовать формулу
, (4.17)
где 
— коэффициент, зависящий от отношения 
. При определении величины коэффициента αH можно пользоваться формулой
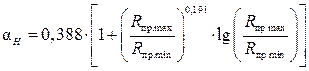. (4.18)
Реально отношение 
может принимать значения от 1 до 100.
Начальное касание тел по линии возникает при контакте цилиндра с плоскостью или двух цилиндров и цилиндра с желобом вдоль образующих. Такое касание деталей на практике встречается достаточно широко. Это контакты рабочих элементов зубчатых и фрикционных передач, роликов с поверхностями беговых дорожек колец подшипников качения, в кулачковых парах и др.
При расчетах, в случае начального касания тел по линии, применяют формулы:
контактное напряжение
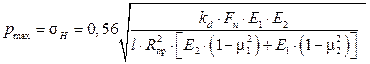; (4.19)
полуширина полоски контакта
; (4.20)
упругое сближение соприкасающихся цилиндрических тел
. (4.21)
При коэффициентах Пуассона µ=0,3 расчет контактного напряжения и полуширины полоски контакта ведется по формулам:
контактное напряжение
; (4.22)
полуширина полоски контакта
. (4.23)
