Лекция 7
Нелинейные уравнения
ВВЕДЕНИЕ
Нелинейные уравнения и системы нелинейных уравнений
Задачи, приводящие к нелинейным уравнениям и системам нелинейных уравнений
В предыдущих лекциях рассматривались линейные уравнения. Во многих приложениях линейные уравнения достаточно эффективны при приближенном описании реального явления.
В частности, наиболее важный для нас метод конечных элементов при применении его к решению задач механики деформируемого твердого тела (МДТТ) приводит к необходимости решения систем линейных алгебраических уравннений. Однако это верно, когда используются уравнения линейной теории упругости.
В одной их очень хороших книг по численным методам [7.1] целая глава носит название «Жизнь, в действительности, нелинейна». В самом деле, даже хорошо известная со школьной скамьи формулировка закона Гука: «Величина перемещения прямо пропорциональна величине вызывающей его силы», оказывается очень приблизительной и неточной моделью реального явления.
Еще современники Гука сомневались в безукоризненности его результатов. Так Гюйгенс (1691) утверждал, что он согласен с результатами Гука, но, только, если пружины будут растянуты незначительно. И в дальнейшем справедливость этого фундаментального закона не раз подвергалась сомнению. В 1849 году Британская Королевская комиссия, «назначенная для того, чтобы исследовать применение железа для железнодорожных сооружений», рекомендовала инженерам впредь заменить линейный закон Гука для железа при растяжении, сжатии и изгибе параболической зависимостью
(7.1)
В общем, на сегодняшний день известно, что даже при малых деформациях соотношения напряжения‑деформации не являются точно линейными.
Если же для решения задач МДТТ использовать нелинейные уравнения, то вместо удобной для решения системы линейных уравнений
(7.2)
будет получена система нелинейных уравнений, которые в лучшем случае удастся представить в следующем виде:
. (7.3)
То есть матрица жесткости является не постоянной, но ее элементы сами зависят от искомых неизвестных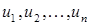 
.
В самом общем случае произвольную систему нелинейных уравнений можно записать следующим образом:
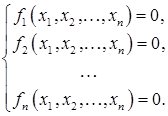(7.4)
Если, ввести векторные обозначения для неизвестных 
и функций 
:
,
то система (7.4) может быть записана проще:
(7.5)
хотя сама задача от этого, к сожалению, не упрощается.
Из сказанного выше вытекает, что одним из возможных источников появления нелинейных систем уравнений могут быть попытки численного решения дифференциальных уравнений.
Еще один возможный источник – задачи оптимизации. Например, при проектировании конструкции крыла самолета логично стремиться к конструкции наименьшего возможного веса (разумеется, при условии выполнения условий по прочности, жесткости и т.п.). Вес конструкции зависит от множества параметров (толщина обшивки, количество нервюр и стрингеров, свойств выбранного материала и многого-многого другого).
То есть вес крыла есть не что иное, как функция многих переменных 
. Между тем, как известно, необходимым условием минимума такой функции является равенство нулю производных функции по ее параметрам:
Если обозначить эти производные, как
то приходим к системе вида (7.4).
Надо сказать, что решение нелинейных уравнений – это проблема, не имеющая на сегодняшний день окончательного решения. Нельзя гарантировать успех даже в получении решения одного уравнения с одной неизвестной. Для систем уравнений – тем более. Однако все-таки, в большинстве случаев удается получить приближенное решение таких задач.
Как всегда, изучение начинаем с наиболее простого случая – одного нелинейного уравнения с одной неизвестной:
(7.6)
Здесь прежде всего следует отметить два важных отличия нелинейных задач от линейных.
1. Любая невырожденная система линейных уравнений имеет единственное решение. Даже такие простые нелинейные уравнения, как 
, или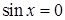 
, могут иметь не одно, а несколько или даже бесконечное множество решений.
2. 
Любая система линейных уравнений может быть точно решена за конечное число арифметических операций. Конечно, при практическом решении СЛАУ в ходе вычислений используется округление результатов. Но потенциальная возможность вычисления без погрешностей округления имеется.
Для нелинейных уравнений ситуация принципиально иная. Около 1830 года Эварист Галуа доказал, что для полинома 5-й степени (и выше) не существует алгебраической формулы. То есть невозможно получить его решение посредством конечного числа алгебраических операций (арифметических операций и извлечения корня).
Между тем самая современная вычислительная техника, в конечном счете, при вычислениях может использовать только перечисленые действия (за исключением корня). Заметим, что полиномы – это не самые сложные из возможных нелинейных уравнений.
То есть возникает тупиковая ситуация: решение нелинейного уравнения имеющимися в настояшее время средствами получить невозможно.
Но, как обычно, когда получить чего-то нельзя, но очень хочется, находятся обходные пути. В данном случае для этого приходится несколько расширить понятие решения уравнения .
Строго говоря, решением уравнения (7.6) является значение 
, которое при подстановке в 
придает этой функции нулевое значение.
Приближенное решение (7.6) можно определить двумя разными способами:
1. 
является приближенным решением уравнения , если 
, где 
, некоторая малая величина (допуск)
2. является приближенным решением уравнения , если 
, где ‑ точное решение
Надо сказать, что оба этих определения не лишены недостатков (см рис.7.1). 
По видимому, хороший алгоритм, должен использовать оба определения. Однако второе определение выглядит несколько противоречивым. В самом деле, если значение точного решения неизвестно, то как можно определить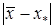 
?
Это противоречие кажущееся. Методы, рассматриваемые далее, дают возможность определенно утверждать, что точное решение находится между двумя значениями 
и 
. При выполнении итераций, расстояние между этими точками уменьшается. Когда, наконец, окажется 
, то любое значение 
из интервала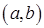 
удовлетворяет второму определения
Еще одна сложность связана с возможной неединственностью решения. Алгоритмы, рассматриваемые далее (см также [7.2]) неплохо работают когда рассматривается интервал на котором имеется один и только один корень. Для произвольной функции и произвольного интервала вполне может возникнуть ситуация, когда на рассматриваемом интервале располагается несколько корней.
В этом случае возникает проблема выделения корней. В литературе можно найти различные рецепты. Чаще всего рекомендуется пройтись по всему интервалу с малым шагом, фиксируя каждую перемену знака . Однако даже этот, в общем, неплохой совет не всегда срабатывает.
Уместно здесь сослаться на авторитетное мнение: «Но вообще отделение корней есть искусство» ([7.3], стр.355).
Метод половинного деления
Пожалуй, самым простым и надежным методом яляется метод половинного деления. В литературе также встречается другое название этого метода – метод бисекций.
Пусть на отрезке 
непрерывная функция , корень которой надо найти, меняет знак (см рис.7.2). Это значит, что на этом отрезке имеется точка , в которой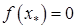 
.
В методе половинного деления очередное приближение (исходными приближениями являются и ) определяется как точка, лежащая посередине, между точками 
и 
:
(7.7)
Для этой точки вычисляется 
и далее определяется, на какой из двух половин отрезка находится корень. В случае приведенном на рисунке – на правой: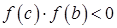 
.
Поэтому повторяем рассуждения для правой половины, положив 
. Приближения продолжаются до тех пор, пока не будет достигнута требуемая точность: 
.
Метод половинного деления отличается высокой надежностью. Правда скорость сходимости его невелика. Оценим количество итераций, которое потребуется для определения корня. Рассмотрим для простоты случай, когда корень ишется на отрезке [0,1]. Пусть точность, которую нам надо обеспечить 0.0001. То есть, мы хотим определить корень с точностью до 4-х значащих цифр. Тогда после первой итерации наш отрезок станет равным 1/2; после второй – 1/4; …; после k-й – 1/2k. Следовательно, необходимая точность будет гарантированно достигнута при 
.
Конечно, при составлении программы надо учитывать возможность попадания очередного приближения на точное значение корня. Хотя такая возможность и маловероятна.
Метод касательных
Метод касательных заключается в том, что каждое очередное приближение определяется путем замены исходной задачи: отыскания корня уравнения на более простую задачу: отыскание корня линейного уравнения.
На рис.7.3 наглядно иллюстрируется идея метода. Сначала выбирается начальное приближение 
. Из точки графика функции для этого значения проводится касательная к графику. Точка пересечения этой касательной с осью абсцисс считается новым приближением. Далее эта операция повторяется до тех пор, пока очередная поправка не окажется меньше требуемой точности.
Таким образом, на каждой итерации решение нелинейного уравнения заменяется решнием линейного уравнения. Из рассмотрения рисунка 7.2 несложно получить соотношение:
И, таким образом, для очередного приближения получается формула:
(7.8)
Эта формула и определяет метод касательных. В литературе этот метод часто назвается методом Ньютона, либо методом Ньютона-Рафсона. Здесь формула (7.8) получена, исходя из наглядных геометрических представлений.
Возможно более строгое получение этой формулы с использованием ряда Тейлора (см, например, [5.2]).
Метод касательных обладает уже значительно большей скоростью сходимости, чем метод половинного деления. Данный метод обладает квадратичной сходимостью. Грубо говоря, это означает, что в результате одной итерации количество правильных значащих цифр удваивается.
То есть, если в начальном приближении имеется одна верная цифра (первая), то после первой итерации таких цифр будет две, а после второй – четыре. Получается, что тот результат, который метод половинного деления давал после 14 итераций в методе касательных может быть достигнут всего за две итерации.
Однако, при высокой скорости сходимости, метод касательных оказывается и более капризным. Возможные неприятности иллюстрируются рисунком 7.4.
То есть при применении этого метода желательно иметь хорошее начальное приближение. Поэтому в хороших программах метод касательных применяется в комбинации с другими методами. Например, после небольшого количества итераций медленным, но надежным методом, далее уточнение решения производится методом касательных.
Метод секущих
Вновь начнем с геометрической иллюстрации (рис.7.5). В этом методе очередная итерация выполняется на основании двух предыдущих приближений.
Для запуска процесса выбираются две точки, ограничивающую область, в которой ищется корень: и . Далее точки графика функции , соответствующие этим значениям аргумента, соединяются прямой.
Точка пересечения прямой с осью абсцисс и является очередным приближением.
Далее определяется, на каком из двух отрезков ([a,c] или [c,b]) происходит перемена знака . (В случае, приведенном на рисунке: [c,b]).
После этого действия повторяются. Итерации продолжаются до тех пор, пока величина выделенного отрезка не станет меньше заданного значения точности.
Для получения формулы, определяющей этот метод, вновь воспользуемся геометрическими соображениями. Уравнение прямой, проходящей через точки 
и 
:
(7.9)
Отсюда следует, что значение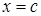 
, при котором 
:
(7.10)
Следует заметить, что формулу (7.10) можно получить из уравнения для метода касательных (7.8). Для этого достаточно в (7.8) вместо производной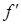 
подставить ее приближенное разностное представление:
Метод секущих сходится медленнее, чем метод касательных. Однако он менее чувствителен к выбору начальных приближений.
Литература
7.1. Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. – М.: Наука, 1986. – 288 с.
7.2. Каханер Д., Моулер К., Нэш С. Численные методы и математическое обеспечение. – М.: Мир, 1998. – 575 с.
7.3.Хемминг Р.В. Численные методы для научных работников и инженеров. – М.: Мир, 1972. – 400 с.
