Пусть функция 
имеет непрерывные частные производные по всем переменным до второго порядка включительно. Поставим часто встречающуюся задачу найти среди функций 
, имеющих на отрезке 
непрерывную производную 
и удовлетворяющих условию
такую, которая является точкой слабого экстремума функционала
При этом на величину 
либо не накладывается никаких ограничений (задача с незакреплённым концом), либо требуется, чтобы выполнялось неравенство 
где 
заданная величина.
Уравнение Эйлера является необходимым условием и для рассматриваемых задач. Действительно, если удалось найти решение 
какой-то из них и положить 
,
то эта функция даёт решение задачи с условиями 
и, следовательно, для неё выполняется уравнение Эйлера.
Предположим, что удалось найти общее решение 
уравнения Эйлера, зависящее от двух произвольных постоянных. Условие даёт одно уравнение. Второе уравнение получаем из следующих условий трансверсальности.
Для задачи, в которой на величину не накладывается никаких ограничений, это условие имеет вид
при 
. (30)
Для задачи с условием 
это условие имеет вид
при и при , если выполнено неравенство 
.
Примечание. В случае задачи с условием 
меняем знаки во всех соответствующих неравенствах.
Рассмотрим пример.
Задача. В двух случаях найти
при условии 
В первом случае конец 
не закреплён. Во втором случае выполнено неравенство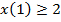 
.
Уравнение Эйлера принимает вид
-x=0
и его общее решение имеет вид
.
Условие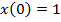 
даёт уравнение 
, так что общее решение принимает вид
. (31)
Из (31) находим
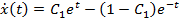. (32)
Так как 
, в первом случае условие трансверсальности даёт 
, откуда, ввиду (32), находим
=0, 
и
Так как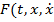 
)= 
выпуклая вверх по совокупности переменных 
функция, задача решена.
Во втором случае из условия 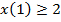получаем
или
. (33)
Если бы выполнялось неравенство 
, то должно выполняться равенство 
, из которого вытекает, что
.
Это неравенство противоречит неравенству (33). Следовательно, 
и
.
При этом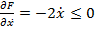 
и поэтому единственным возможным решением является
Так как 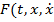)= выпуклая вверх по совокупности переменных функция, и эта задача решена.
Задача. Найти решение задачи с незакреплённым концом:
Решение. Уравнение Эйлера для этой задачи:
=0.
Его общее решение имеет вид
,
где 
. Условие 
даёт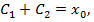 
откуда
Из условия трансверсальности находим 
, т.е.
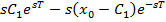=0,
откуда
и
Так как )=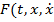 
выпуклая вниз по совокупности переменных функция, задача решена.
Замечание. Рассмотренная задача связана с математической моделью макроэкономической задачи планирования экономики.
Замечание. Также следует отметить, что в курсах вариационного исчисления задача с подвижными границами обычно рассматривается в более общей постановке. Требуется, чтобы концы гладких кривых лежали на двух заданных линиях 
. Условия трансверсальности при этом имеют вид
.
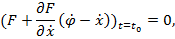
