Исследуемые закономерности

Лабораторная работа 11

Скатывание тела с наклонной плоскости

Цель работы: проверка выполнимости основного уравнения динамики вращательного движения (уравнения моментов) и закона сохранения механической энергии в опыте по скатыванию тела круглой формы с наклонной плоскости.

Приборы и принадлежности: Установка представляет собой наклонную плоскость 1, которую с помощью винта 2 можно устанавливать под разными углами 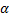к горизонту (рис.1). Угол 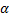измеряется с помощью шкалы 3. На плоскость может быть помещен ролик 4. В комплект работы входит два ролика разной массы. Для удержания ролика в верхней точке используется электромагнит 5, управление которым осуществляется с помощью электронного секундомера СЭ-1. Пройденное роликом расстояние измеряется линейкой 6, закрепленной вдоль плоскости. Время скатывания ролика измеряется автоматически с помощью датчика 7, выключающего секундомер в момент касания роликом финишной точки. Установка имеет два режима работы, регулируемых тумблером «плоскость»/ «удар», находящимся в ее нижней части слева.

Исследуемые закономерности

Основной закон динамики вращательного движения или уравнение моментов может быть записан в разных формах: в терминах углового ускорения вращения тела, в дифференциальной и интегральной форме

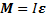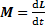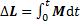, , (1)

где – результирующий момент всех внешних сил, действующих на него, – момент импульса тела, – его момент инерции, являющийся аналогом массы или мерой инертности тела при его вращательном движении. Момент импульса тела может быть представлен в ви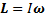де , где 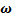– угловая скорость его вращения.

Все моменты (силы, импульса и инерции) зависят от того, относительно какой произвольной точки (полюса) или оси вращения они рассчитываются. Однако равенство правых и левых частей уравнений (1) при этом не нарушается. В справочниках приводятся только моменты инерции 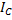тел относительно осей вращения, проходящих через его центр масс (ЦМ) C. Если другая ось вращения тела параллельна оси, проходящей через ЦМ тела, и смещена от нее на расстояние 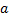, то момент инерции тела относительно новой оси вращения рассчитывают по теореме Штейнера: 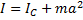, где – масса тела.

В данной работе изучается качение круглых тел по наклонной плоскости. Момент инерции круглого тела относительно оси, проходящей через его ЦМ вдоль оси его симметрии равен 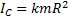, где – радиус тела, – коэффициент инерции, равный для шара 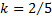, для сплошного цилиндра (диска) , для полого цилиндра (обруча) . Если тело катится по поверхности, то его момент инерции относительно точки О касания тела и поверхности по теореме Штейнера равен : .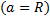

 

 

S	V	a	m	p	F
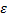
			I	L	M

Существует аналогия между параметрами, описывающими поступательное и вращательное движение тела, которая дается таблицей:

Смысл входящих в таблицу параметров понятен по их обозначениям. Эта таблица позволяет переходить от уравнений поступательного движения к уравнениям вращательного движения. Так, уравнения и 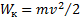переходят в уравнения 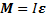и .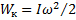

Рассмотрим скатывание тела круглой формы с наклонной плоскости. Для описания движения используем первое уравнение (1). Считаем, что в точке О касания тела и плоскости нет проскальзывания. Мгновенная скорость точки О в этом случае относительно плоскости в любой момент времени равна нулю 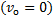. Ось вращения, проходящую через такую точку называют мгновенной осью вращения.

 

Рис.2

Для описания движения тела возьмем полюс в точке О касания тела и плоскости (рис.2), через которую проходит мгновенная ось вращения тела (проскальзывание тела относительно плоскости отсутствует). Относительно этой точки моменты сил N и 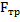равны нулю: 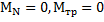, а момент силы тяжести равен . Момент инерции круглого тела относительно оси О по теореме Штейнера , угловое ускорение вращения тела . Тогда уравнение вращательного движения тела относительно оси, проходящей через точку О 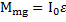, примет вид 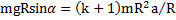. Отсюда ускорение скатывания тела .

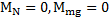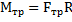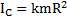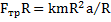Если выбрать полюс в точке С (ЦМ тела), то моменты сил N и mg относительно оси, проходящей через точку С, будут равны нулю: , а момент силы трения будет равен . Момент инерции тела относительно оси С равен , а угловое ускорение его вращения .Тогда уравнение вращательного движения тела относительно оси С примет вид . Откуда 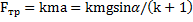. Силу трения можно также найти из второго закона Ньютона для ЦМ тела: 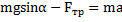. Результат будет прежним.

Силу трения качения можно формально представить в виде, аналогичном для силы трения скольжения 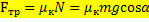, где величину можно назвать коэффициентом трения качения. В отличие от коэффициента трения скольжения он зависит от угла наклона плоскости.

Для описания скатывания тела с наклонной плоскости можно также использовать энергетический подход. Кинетическая энергия катящегося тела, совершающего поступательно вращательное движение, с учетом 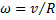, а также 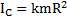и 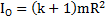равна

.

Работы силы нормальной реакции опоры N, а также силы трения качения 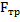(нет проскальзывания) равны нулю 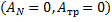, поэтому в системе имеет место закон сохранения механической энергии: или 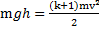. Откуда скорость тела, скатившегося с высоты 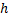, в основании наклонной плоскости равна 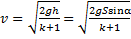, где S – путь, проходимый телом вдоль наклонной плоскости.

В данной работе по измеренному времени t скатывания тела с наклонной плоскости определяются его ускорение скатывания 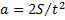и скорость в конце наклонной плоскости 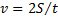, которые сопоставляются с их теоретическими значениями, рассчитываемыми по формулам и 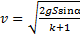. Затем делается заключение о выполнимости уравнения вращательного движения и закона сохранения механической энергии.