Федеральное государственное образовательное бюджетное
учреждение
высшего профессионального образования
Московский технический университет связи и информатики
Кафедра теории вероятностей и прикладной математики
Методические указания
и задания на контрольные работы
по дисциплине
МАТЕМАТИКА
Для студентов-заочников 1 курса
направлений 15030400, 09030200
Москва 2016
План УМД на 2015/2016 уч. г.
Методические указания
и задания на контрольные работы
по дисциплине
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Составитель: А.В.Власов, кандидат технических наук, доцент
Издание утверждено на заседании кафедры. Протокол № __ от..2016 г.
Рецензент Е.А.Скородумова, кандидат физико-математических наук, доцент
Целю преподавания данной дисциплины является изучение основных разделов математического анализа, включающих в себя теорию пределов, а также основы дифференцирования и интегрирования элементарных функций. Полученные студентами знания, умения и навыки по данной дисциплине помогут им в освоении таких дисциплин как «Теория вероятностей и математическая статистика», «Статистика», а также ряд иных дисциплин.
В процессе изучения курса студент должен самостоятельно выполнить контрольную работу, вариант которой приводятся в конце данного пособия. По результатам самостоятельной работы и на основании выполненной им контрольной работы, студент допускается к зачету по данному курсу.
Бюджет времени на изучение курса (час)
| Форма обучения | Распределение часов | ||||
| Очная | Заочная | 1 семестр | |||
| Очные занятия | Самостоятельная работа | Лекции | Упражнения | Отчет | |
| Зачет |
Примерное содержание лекционного курса
1. Функции. Основные способы задания функций. Основные элементарные функции и их графики.
2. Предел функции. Основные теоремы о пределах. Замечательные пределы. Непрерывность функции. Классификация точек разрыва.
3. Производная и дифференциал, их геометрический смысл. Основные правила вычисления производной. Таблица производных элементарных функций.
4. Производная сложной функции. Производная функций, заданных неявно.
5. Неопределенный интеграл, его свойства. Таблица основных неопределенных интегралов. Интегрирование методами замены переменной и по частям.
6. Интегрирование рациональных и иррациональных дробей.
7. Определенный интеграл. Формула Ньютона – Лейбница.
8. Геометрическое и физическое применение производной и определенного интеграла. Построение уравнения касательной. Задачи определения минимума (максимума). Вычисление площадей с помощью определенного интеграла.
Примерная тематика упражнений
1. Вычисление пределов.
2. Вычисление производных. Производная сложной функции. Производная неявной функции.
3. Вычисление неопределенных интегралов. Интегрирование методами замены переменной и по частям.
4. Определенный интеграл. Методы замены переменной и интегрирования по частям в определенном интеграле.
5. Использование производной и определенного интеграла для решения физических и геометрических задач. Уравнение касательной. Вычисление площадей плоских фигур при помощи определенного интеграла.
Список литературы:
Основная:
1. Демидович Б.П. Краткий курс высшей математики: Учебное пособие для вузов.– М.: Астрель, 2004.– 654с.
2. Данко П.Е. Высшая математика в упражнениях и задачах. В 2-ух частях. Часть 1.–М.: ОНИКС, 2005.–304с.
Дополнительная:
3. Щипачев В.С. Математический анализ.– М.: Высшая школа, 2001.–176с.
4. Сборник задач по высшей математике для экономистов /Под ред. Ермакова В.И. и др.– М.: ИНФРА-М, 2003, 2004.– 575с.
Пример решения задач варианта контрольной работы
по курсу «Математика»
Задача 1а. Найти предел функции 
Решение. Убеждаемся, что в результате непосредственной подстановки предельного значения получается неопределенность вида 
. Делим числитель и знаменатель рациональной дроби на переменную в наивысшей степени, то есть, в данном случае, на 
. Учитывая, что 
и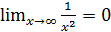 
, а также используя ряд свойств пределов, получаем:
Задача 1б. Найти предел функции:
.
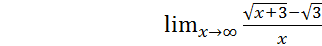Решение. Данное выражение представляет собой неопределенность вида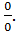 
Выражения 
называется для выражения 
сопряженным, а умножение данного выражения на сопряженное позволяет избавиться в этом выражении от радикалов:
(
) 
(
- 
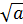Таким образом, домножая числитель и знаменатель дроби на выражение, сопряженное числителю, получим:
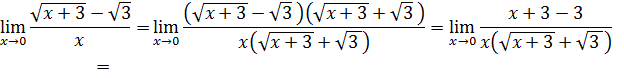
Задача 1в. Найти предел функции: 
Решение: Убедимся сначала, что данное выражение представляет собой неопределенность вида 
. Далее вычислим указанный предел, приводя его ко второму замечательному пределу, записанному в виде:
Задача 2а. Вычислить производную функции 
.
Решение. Данная функция является произведением двух функций. Поэтому, используя формулу дифференцирования произведения
= 
и формулы дифференцирования элементарных функций получим:
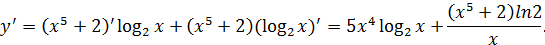
Задача 2б. Вычислить производную сложной функции
).
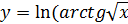Решение. При вычислении производной сложной функции прежде всего надо понять порядок применения последовательности функций к аргументу 
. Так, в данной функции сначала из аргумента извлекается квадратный корень, далее от полученного значения вычисляется арктангенс, и, наконец, вычисляется натуральный логарифм. Вычисление производной происходит в обратном порядке, то есть, начиная с логарифма:
, где 
.
Таким образом, мы получаем следующую цепочку равенств:
= 
=
= 
.
Задача 2в. Вычислить производную функции 
.
Решение. Преобразуем данную функцию к виду, удобному для дифференцирования, использовав основное логарифмическое тождество 
.
Получим:
.
Далее, использовав алгоритм дифференцирования сложной функции, а также формулу дифференцирования произведения, получим:
).
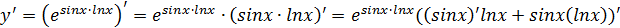
Задача 3а. Вычислить неопределенный интеграл: 
.
Решение. Используем для вычисления этого интеграла метод замены переменной, введя новую переменную 
В этом случае 
, откуда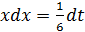 
. Делая замену переменной в неопределенном интеграле и используя таблицу неопределенных интегралов, получим:
Возвращаясь к старой переменной, получим ответ: 
Задача 3б. Вычислить неопределенный интеграл: 
.
Решение. Используем формулу интегрирования по частям в виде:
.
Введем обозначения: 
. Тогда: 
.
Подставляя все введенные и полученные функции в формулу интегрирования по частям, получим: =-(4 
.
Задача 4. Вычислить определенный интеграл 
.
Решение. Сделаем замену 
Тогда 
= 
, а значит 
. При этом надо учитывать возможное изменение пределов интегрирования при замене переменной. В нашем случае нижний предел интегрирования 
=1 переходит в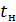 
= 
, верхний предел 
переходит в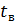 
= 
, а интеграл в результате замены переменной интеграл принимает вид:
= 
= 
=ln 
.
Задача 5. Число 20 разбить на такие два слагаемых, что бы сумма их квадратов была наименьшей.
Решение. Пусть 
. Запишем целевую функцию 
и найдем ее минимум. Преобразуем функцию к виду 
и вычислим ее производную: 
. Приравняв ее к нулю, получим критическую точку 
=10. Так как вторая производная в точке положительна (
при всех 
это значит, что функция имеет в этой критической точке минимум. Таким образом, искомое представление 20=10+10.
Правила нахождения номера своего варианта.
А. Если две последние цифры студенческого билета образуют число, меньше 50, то номер варианта совпадает с этим числом.
Например, если номер студенческого билета БСТ1323, то номер варианта 23.
В. Если две последние цифры студенческого билета образуют число больше или равное 50, то для получения номера варианта из этого числа надо вычесть 50.
Например, если номер студенческого билета БСТ1368, то номер варианта 68-50=18.
