динамика вращательного движения

Момент инерции материальной точки

,

где m - масса точки, r - расстояние от оси вращения.

Момент инерции твердого тела

где - расстояние элемента массы от оси вращения.

При непрерывном распределении массы

Теорема Штейнера: момент инерции тела относительно произвольной оси равен

,

где - момент инерции тела относительно оси, проходящей через центр тяжести параллельно заданной оси, a - кратчайшее расстояние между осями, m - масса тела.

, где l - длина стержня, ось перпендикулярна стержню.

, где R - радиус диска, ось перпендикулярна плоскости основания.

, где R - радиус шара.

, где R - радиус кольца, ось перпендикулярна плоскости кольца.

Момент импульса вращающегося тела

где - угловая скорость.

Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси

где M - момент результирующей силы, действующей на тело.

где F - сила, h - плечо силы - кратчайшее расстояние от оси до линии действия силы.

При J=const

где - угловое ускорение.

Закон сохранения момента импульса:

,

где - момент импульса i -го тела, входящего в состав замкнутой системы.

 

примеры решения задач

 

Задача 1. По наклонной плоскости, образующей угол a с горизонтом, скатывается без скольжения 1) сплошной однородный диск, 2) шар. Определить линейное ускорение их центров. Предварительно вывести общую формулу.

Тело участвует в сложном движении:

1) поступательно движется вниз по наклонной плоскости; 2) вращается вокруг оси, проходящей через центр тяжести.

На рисунке покажем силы, действующие на тело.

Для поступательного движения запишем II закон Ньютона в проекциях на ось OX.

. (1)

Для вращательного движения используем закон

, (2)

где - момент инерции, - угловое ускорение.

Момент силы создает сила трения, плечо которой равно R, две другие силы не создают вращающего момента.

.

Перепишем (2):

.

Выразим силу трения из (3) и подставим в (1):

Отсюда

. (4)

Зная моменты инерции диска и шара

,

найдем ускорения диска и шара

,

Ответ: ,

 

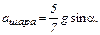
Задача 2. Вертикальный столб высотой подпиливается у основания и падает на землю, поворачиваясь вокруг основания. Определить линейную скорость его верхнего конца в момент удара о землю. Трением пренебречь.

На рисунке C- центр тяжести столба. Применим закон сохранения механической энергии. Масса распределена равномерно, поэтому в выражении для потенциальной энергии при вертикальном положении столба возьмем высоту его центра тяжести относительно нулевого уровня отсчета: .

В горизонтальном положении столб приобретает кинетическую энергию

где J - момент инерции относительно оси, проходящей через неподвижный конец, w - угловая скорость.

. (1)

По теореме Штейнера

.

Угловую скорость выразим через линейную скорость упавшего конца:

.

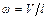Подставив и в (1), найдем

.

Ответ: .

 

Задача 3. Стержень массой и длиной может свободно вращаться вокруг неподвижной оси, проходящей через его верхний конец. Стержень отклоняют в горизонтальное положение и отпускают. Проходя через вертикальное положение, нижний конец стержня упруго ударяет о малую шайбу массой . Определить скорость шайбы после удара.

 

O

 

Нулевой уровень отсчета потенциальной энергии проведем через центр тяжести стержня С при вертикальном положении стержня. Запишем закон сохранения механической энергии для стержня до удара.

(1)

где , - угловая скорость стержня.

Для описания упругого соударения стержня с шайбой используем закон сохранения момента импульса

(2)

и закон сохранения механической энергии

. (3)

В уравнении (2) mVl - момент импульса шайбы. Напомним, что для материальной точки У шайбы r = l,

Перепишем (2) и (3):

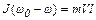; (4)

. (5)

Разделив (5) на (4), найдем связь между и :

. (6)

Подставив (6) и в (4), получим

. (7)

Используем (2), тогда (7) примет вид

Ответ:

 

задачи для самостоятельного решения

 

4.1. Через блок в виде однородного сплошного диска, имеющего массу m = 500 г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m₁ = 100 г и m₂ = 120 г. С каким ускорением будут двигаться грузы, если ихпредоставить самим себе? Трением на оси блока пренебречь.

4.2. Вал массой m = 100 кг и радиусом R = 5 см вращается с частотой ν = 8 с^-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F = 40 Н, под действием которой вал остановился через время τ = 10 с. Определить момент и коэффициент силы трения.

4.3. За какое время t скатится без скольжения обруч с наклонной плоскости длиной l = 2 м и высотой h = 10 см?

4.4. Шар массой m = 10 кг и радиусом R = 20 см вращается вокруг оси, проходящей через его центр. Зависимость угла поворота от времени имеет вид φ = А + Bt² + Сt³, где В = 4 рад/с², С = - 1 рад/с³. Найти закон изменения момента сил, действующего на шар. Определить момент сил спустя время τ = 2 с после начала движения шара.

4.5. Тонкий однородный стержень длиной l = 50 см и массой m = 40 г вращается с угловым ускорением ε = 3 рад/с² вокруг горизонтальной оси, проходящей перпендикулярно стержню: 1) через его середину, 2) через один из его концов. Определить вращающий момент для этих случаев.

4.6. Два тела массами m₁ = 0,25 кг и m₂ = 0,15 кг связаны тонкой нитью, перекинутой через блок. Блок укреплен на краю горизонтального стола, по поверхности которого скользит тело массой m₁. С каким ускорением движутся тела? Коэффициент трения тела массой m₁ о поверхность стола μ = 0,3. Масса блока m₀ = 0,1 кг, и ее можно считать равномерно распределенной по объему блока. Массой нити и трением в подшипниках оси блока пренебречь.

4.7. Через неподвижный блок массой m = 0,2 кг перекинут шнур, к концам которого подвесили грузы массами m₁ = 0,3 кг и m₂ = 0,5 кг. Определить силы натяжения шнура Т₁ и Т₂ по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу.

4.8. Маховик в виде однородного диска массой m = 100 кг и радиусом R = 40 см вращался с частотой n = 480 об/мин. Определить момент тормозящей силы, если после начала действия этой силы маховик остановился через время τ = 80 с.

4.9. На шкив радиусом R = 10 см намотана нить, к концу которой привязан груз массой m = 2 кг. Груз опускается со скоростью, меняющейся по закону V = 2 – 8 t (м/с). Найти момент инерции шкива относительно оси вращения. Трением пренебречь.

4.10. Однородный сплошной цилиндр массой m₀ = 5 кг и радиусом R = 20 см может без трения вращаться вокруг неподвижной горизонтальной оси. На цилиндр намотан тонкий нерастяжимый шнур, к которому прикреплён груз массой m₁ = 3 кг. Найти угловое ускорение цилиндра и расстояние, пройденное грузом массой m₁ за первые две секунды движения.

4.11. Через блок в виде однородного сплошного диска массой m₀ = 3 кг, радиусом R = 10 см перекинута невесомая нить, к концам которой привязаны грузы массами m₁ = 2 кг и m₂ = 1 кг. Определить угловое ускорение блока. Трением на оси блока и проскальзыванием нити по блоку пренебречь.

4.12. Маховик, момент инерции которого J = 69,6 кг×м², вращается с угловой скоростью ω = 31,4 рад/с. Найти тормозящий момент М, под действием которого маховик останавливается через время τ = 20 с.

4.13. Через блок перекинута невесомая нить, к концам которой привязаны два груза. Груз массой m₂ = 5 кг поднимается со скоростью, меняющейся по закону V = 5 + 0,8 t (м/с), груз массой m₁ опускается. Момент инерции блока J= 5×10^{-2 кг}×м², его радиус R = 0,2 м. Найти массу опускающегося груза m₁. Трением пренебречь.

4.14. На цилиндр радиусом R = 40 см намотана нить, к концу которой подвешен груз массой m. Груз начал опускаться и за t = 4 с прошел путь h = 2 м. Какова масса груза? Момент инерции цилиндра J_ц = 1,53 кг×м².

4.15. На барабан радиусом R = 0,5 м намотан шнур, к которому привязан груз массой m = 10 кг. Найти момент инерции барабана, если известно, что груз опускается с ускорением а = 2,04 м/с².

4.16. Вал массой m = 150 кг и радиусом R = 6 см вращался, делая 9 оборотов в секунду. К цилиндрической поверхности вала прижали тормозную колодку ссилой F = 50 Н, и через t = 10 с вал остановился. Определить коэффициент трения m.

4.17. Колесо (обруч и 2 стержня) пустили со скоростью V₀ = 2 м/с. За какое время колесо остановится под действием тормозящей силы F = 5 Н? Масса обруча m₁ = 3 кг, масса одного стержня m₂ = 3 кг.

4.18. На барабан радиусом R = 20 см с моментом инерции J = 0,1 кг×м² намотан шнур, к которому привязан груз массой m = 0,5 кг. До начала вращения барабана груз находился на высоте h = 1 м над полом. За какое время t груз опустится до пола?

4.19. Угол поворота стержня вокруг оси, проходящей через его центр, задан уравнением φ = At + Bt³, где B = 0,2 рад/с³, А = 2 рад/с. Определить вращающий момент М, действующий на стержень спустя время τ = 2 с после начала движения. Момент инерции стержня J = 0,048 кг×м².

4.20. Блок, имеющий форму диска массой m = 0,4 кг, вращается под действием сил натяжения нити, к концам которой подвешены грузы массами m₁ = 0,3 кг и m₂ = 0,7 кг. Определить силы натяжения нити Т₁ и Т₂ по обе стороны блока.

4.21. К ободу однородного сплошного диска радиусом R = 0,5 м приложена постоянная касательная сила F= 100 Н. При вращении диска на него действует момент сил трения М = 2 Н×м. Определить массу m диска, если известно, что его угловое ускорение постоянно и равно ε = 12 рад/с².

4.22. При торможении частота вращающегося колеса уменьшилась от n₁ = 300 об/мин до n₂ = 180 об/мин за время t = 1 мин. Определить момент силы торможения. Момент инерции колеса J = 2 кг×м².

4.23. В медном диске радиусом R = 5 см и толщиной h = 1 мм сделаны симметрично относительно его центра два круглых выреза радиусом г = 2 см каждый, причем их центры удалены от центра диска на расстояние а = 2,5 см. Определить момент инерции диска с вырезами относительно оси, перпендикулярной плоскости диска и проходящей через его центр. Плотность меди ρ = 8,9 г/см³.

4.24. Определить момент инерции цилиндрической муфты относительно оси, совпадающей с ее осью симметрии, масса муфты m = 2 кг, внутренний радиус г = 3 см, внешний - R = 5 см.

4.25. Определить момент инерции полого шара массой m = 0,5 кг относительно оси, проходящей через центр. Внешний радиус шара R = 0,02 м, внутренний - г = 0,01 м.

4.26. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек массой m₁ = 60 кг. На какой угол повернется платформа, если человек пойдет вдоль её края и, обойдя его, вернется в исходную точку? Масса платформы m₂ = 240 кг. Момент инерции человека рассчитывать так же, как для материальной точки.

4.27. На горизонтальной скамье Жуковского (однородный диск, который может вращаться с малым трением относительно вертикальной оси, проходящей через его центр) стоит человек и держит в руках стержень длиной l= 2,4 м и массой m = 8 кг, расположенный вертикально по оси вращения скамьи. Скамья с человеком вращается с частотой ν = 1 с^-1. С какой частотой будет вращаться скамья с человеком, если он повернет стержень в горизонтальное положение? Суммарный момент инерции человека и скамьи J = 6 кг×м².

4.28. На краю горизонтальной платформы, имеющей форму диска радиусом R = 2 м, стоит человек массой m₁ = 80 кг. Масса платформы m₂ = 240 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью ω будет вращаться платформа, если человек будет идти вдоль ее края со скоростью V = 2 м/с относительно платформы.

4.29. Диск массой m₁ = 10 кг с лежащим на его краю шариком массой m₂ = 1 кг вращается с частотой n₁ = 10 об/мин относительно оси, проходящей через его центр. Шарик перекатывается в центр диска. Найти частоту n₂.

4.30. Однородный стержень длиной l = 2 м и массой m = 8 кг подвешен за один конец и может вращаться без трения вокруг горизонтальной оси. В середину стержня ударилась и застряла в нем пуля массой m₁ = 10 г, летевшая со скоростью V = 800 м/с. На какой угол отклонился стержень?

4.31. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой n = 20 об/мин. В центре платформы стоит человек и держит в вытянутых руках гири. Какой станет частота вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от J₁ = 2,94 кг×м² до J₂ = 0,98 кг×м²? Считать платформу круглым однородном диском.

4.32. Кинетическая энергия вращающегося маховика равна E = 1000 Дж. Под действием постоянного тормозящего момента маховик начал вращаться равнозамедленно и, сделав N = 80 оборотов, остановился. Определить момент силы торможения M.

4.33. Маховик, момент инерции которого равен J = 4,0 кг×м², начал вращаться равноускоренно из состояния покоя под действием момента силы М = 20 Н×м. Вращение продолжалось в течение времени t = 10 с. Определить кинетическую энергию, приобретенную маховиком.

4.34. Тонкий прямой стержень длиной l = 1 м прикреплен к горизонтальной оси, проходящей через его конец. Стержень отклонили на угол a = 60⁰ от вертикали и отпустили. Определить линейную скорость V нижнего конца стержня в момент прохождения через положение равновесия.

4.35. Однородный стержень длиной l = 85 см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую наименьшую скорость V надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?

4.36. Горизонтально летевшая пуля попала вертикальный однородный стержнь массой m = 210 кг и длиной l = 1 м и застряла в нем. Стержень может свободно вращаться вокруг точки закрепления верхнего конца в шарнире. Пуля имела импульс Р = 3 кг×м/с и попала в стержень на расстоянии l = 20 см от точки закрепления стержня. Найти угловую скорость w, которую приобретет стержень с пулей.

4.37. На какой угол a надо отклонить однородный стержень, подвешенный на горизонтальной оси, проходящей через верхний конец стержня, чтобы нижний конец стержня при прохождении им положения равновесия имел скорость V = 5 м/с? Длина стержня l = 1 м.

4.38. Платформа в виде диска вращается по инерции около вертикальной оси с частотой n₁ = 14 об/мин. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота вращения возросла до n₁ = 25 об/мин. Масса человека m = 70 кг. Определить массу платформы M. Момент инерции человека рассчитывать так же, как и для материальной точки.

4.39. Маховик в виде сплошного однородного диска массой m = 80 кг и радиусом R = 30 см находится в состоянии покоя. Какую работу требуется совершить, чтобы привести диск во вращение с частотой n = 10 об/с? Какую работу пришлось бы совершить при этом, если бы диск при той же массе имел вдвое больший радиус?

4.40. Карандаш длиной l= 15 см, поставленный вертикально, падает на стол. Какие угловую w и линейную V скорости будет иметь в конце падения: 1) середина карандаша; 2) верхний его конец? Нижний конец карандаша не проскальзывает.

4.41. Определить линейную скорость V центра шара, скатившегося без скольжения с наклонной плоскости высотой h = 1 м.

4.42. Однородный диск вкатывается в горку с начальной скоростью V₀ = 12 км/ч. Определить угол наклона горки α, если до полной остановки диск пройдет по горке расстояние l = 2 м.

4.43. Вентилятор вращается с частотой n = 900 об/мин. После выключения он сделал до остановки N = 75 оборотов. Работа сил торможения равна A = 44,4 Дж. Найти: 1) момент инерции вентилятора J; 2) момент силы торможения M.

4.44. Какой путь пройдет катящийся без скольжения диск, поднимаясь вверх по наклонной плоскости с углом наклона a = 30⁰, если ему сообщена начальная скорость V = 7 м/с, направленная вдоль наклонной плоскости?

4.45. Диск массой m₁ = 5 кг и радиусом R = 5 cм, вращающийся с частотой n = 10 об/мин, приводится в сцепление с неподвижным диском массой m₂ = 10 кг такого же радиуса. Определить энергию, которая пойдет на нагревание дисков, если при их сцеплении скольжение отсутствует. Диски имели общую ось вращения после сцепления.

4.46. Диск радиусом R = 10 см и массой m = 2 кг вращается с частотой ν = 2 об/с вокруг оси, проходящей через его центр. Какую работу надо совершить, чтобы увеличить частоту вращения диска вдвое?

4.47. Шарик массой m = 60 кг, привязанный к концу нити длиной
l₁ = 1,2 м, вращается в горизонтальной плоскости счастотой n₁ = 2 об/с. Нить укорачивается, приближая шарик к оси вращения до расстояния l₂ = 0,6 м. С какой частотой n₂ будет при этом вращаться шарик? Какую работу совершает внешняя сила, укорачивая нить?

4.48. Шар и диск, двигаясь с одинаковой скоростью, вкатываются вверх по наклонной плоскости. Какое из тел поднимается выше? Найти отношение высот подъема.

4.49. Маховик вращается с частотой n = 10 об/с, его кинетическая энергия равна Т = 7,85 кДж. За какое время t вращающий момент М = 50 Н×м, приложенный к этому маховику, увеличит угловую скорость маховика в два раза?

4.50. Колесо начинает вращаться с постоянным угловым ускорением ε = 0,5 рад/си через время t₁ = 15 с после начала движения приобретает момент импульса L = 73,5 кг×м²/с. Найти кинетическую энергию колеса через t₂ = 20 с после начала вращения.

 

 

5. механические колебания

Уравнения гармонических колебаний:

x=Acos(wt+j₀), x=Asin(wt+j₀), или их линейная комбинация,

где x - смещение точки от положения равновесия, A - амплитуда, wt+j₀ - фаза колебаний в момент времени t, w - циклическая частота, j₀ - начальная фаза.

где u и T - частота и период.

Дифференциальное уравнение свободных колебаний материальной точки:

или

где , m - масса точки, k - коэффициент квазиупругой силы.

Полная энергия точки, совершающей гармонические колебания,

Период колебаний тела, подвешенного на пружине (пружинный маятник),

где m - масса тела, k - жесткость пружины.

Период колебаний математического маятника

где l - длина нити, g - ускорение свободного падения.

Период колебаний физического маятника

где J - момент инерции тела относительно оси колебаний, a - расстояние центра масс маятника от оси колебаний.

Дифференциальное уравнение затухающих колебаний

или ,

где c - коэффициент сопротивления, d - коэффициент затухания, - собственная циклическая частота колебаний.

Уравнение затухающих колебаний (частное решение дифференциального уравнения):

где A₀ - амплитуда колебаний в момент времени t=0,

A(t) - амплитуда затухающих колебаний в момент времени t.

Декремент затухающих колебаний

Логарифмический декремент колебаний

где T - период.

примеры решения задач

 

Задача 1. Математический маятник длиной l₁=40 см и физический маятник в виде тонкого прямого стержня длиной l₂=60 см синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние a центра масс стержня от оси колебаний.

При синхронном колебательном движении маятников их периоды равны ,

где .

Отсюда

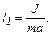(1)

Момент инерции физического маятника определяется по теореме Штейнера:

(2)

Подставив (2) в (1), получим квадратное уравнение

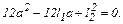(3)

Из (3) найдем два корня: a₁=10 см, a₂=30 см.

Таким образом, при одном и том же периоде колебаний физического маятника возможны два варианта расположения оси.

Величину (1) называют приведенной длиной физического маятника.

Ответ: a₁=10 см, a₂=30 см.

Задача 2. Найти уравнение, связывающее модуль импульса P_x и координату x одномерного гармонического осциллятора. Масса осциллятора m₁, циклическая частота w₀, амплитуда колебаний A.

Запишем уравнение гармонических колебаний

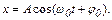(1)

Тогда

(2)

Выразим из (1) а из (2) ,

(3)

(4)

Возведем (3) и (4) в квадрат и сложим. Учитывая, что

получим

- уравнение эллипса.

Ответ: .

 

Задача 3. Математический маятник совершает малые колебания в среде, в которой коэффициент затухания 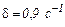. Определить время по истечении которого амплитуда маятника уменьшится в пять раз.

Вследствие трения колебания маятника будут затухающими:

где j - угол отклонения нити маятника от вертикали в момент времени t, при t=0, j=0.

Амплитуда затухающих колебаний изменяется со временем по экспоненциальному закону

. (1)

Запишем (1) для моментов времени t и t+t:

, .

Отношение амплитуд

. (2)

Логарифмируя (2), найдем

.

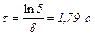Ответ: t=1,79 с.

задачи для самостоятельного решения

 

5.1. Под действием грузика пружина растянулась на Dx = 9 см. Определить период собственных колебаний T этой системы.

5.2. Найти отношение длин двух математических маятников, если отношение их периодов Т₁/ Т₂ = 1,5.

5.3. Математический маятник установлен в лифте, который подни­мается с ускорением a = 2,5 м/с². Определить период T собственных колеба­ний маятника. Его длина равна 1 м.

5.4. Лифт, в котором колеблется математический маятник, опускается с ускорением a = 3 м/с². Определить период колебаний T маятника. Его длина равна 1 м.

5.5. Грузик массой m подвешен к двум пружинам, соединённым "последовательно". Определить частоту колебаний груза. Коэффициенты жесткости пружин равны k₁ и k₂.

5.6. Грузик массой m подвешен к двум пружинам, соединенным "параллельно". Определить частоту колебаний груза. Коэффициенты жесткости пружин равны k₁ и k₂.

5.7. Медный шарик, подвешенный к пружине, свободно колеблется. Как изменится период колебаний этой системы, если вместо медного подвесить алюминиевый шарик таких же размеров?

5.8. На стержне длиной l = 30 см закреплены два одинаковых грузика: один - в середине стержня, другой - на одном из его концов. Эта система может свободно вращаться около горизонтальной оси, проходящей через свободный конец стержня. Определять период собственных колебаний T этого физического маятника. Массой стержня пренебречь.

5.9. На стержне длиной l = 30 см и массой m = 1 кг, закреплены два одинаковых грузика: один - в середине стержня, другой - на одном из его концов. Эта система может свободно вращаться около горизонтальной оси, проходящей через свободный конец стержня. Определять период собственных колебаний T этого физического маятника.

5.10. Диск радиусом R = 20 см может свободно вращаться вокруг горизонтальной оси, проходящей через середину радиуса перпендикулярно его плоскости. Определить частоту n собственных колебаний этого физического маятника.

5.11. Однородный стержень массой m и длиной lможет свободно вращаться вокруг горизонтальной оси, проходящей через его конец. Определить частоту собственных колебаний стержня.

5.12. Однородный стержень массой m, длиной l может свободно вращаться вокруг горизонтальной оси, проходящей на расстоянии l/4 от одного из его концов. Определить период колебаний этого физического маятника.

5.13. На горизонтальном столе лежит шар массой 200 г, прикрепленный к горизонтально расположенной пружине жесткостью 500 Н/м. В шар попадает пуля массой 10 г, летящая горизонтально со скоростью 300 м/с, и застревает в нем. Определить амплитуду и период колебаний шара. Перемещением шара во время удара, сопротивлением воздуха и тре­нием между поверхностью шара и стола пренебречь.

5.14. Однородный стержень массой 0,5 кг и длиной l м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В противоположный конец стержня попадает пуля массой 10 г, летящая горизонтально со скоростью 300 м/с, и застревает в нем. Определить амплитуду и период колебаний стержня.

5.15. Однородный стержень может вращаться вокруг горизонтальной оси, проходящей на расстоянии 1/4 от одного из его концов. В противоположный конец попадает пуля массой 10 г, летящая горизонтально со скоростью 200 м/с, и застревает в нем. Определить амплитуду и период колебаний стержня. Масса стержня 0,5 кг, длина 1 м.

5.16. За 5 мин амплитуда математического маятника уменьшилась в 2раза. За какой промежуток времени его амплитуда уменьшится в 8 раз?

5.17. Математический маятник длиной 1 м колеблется в воздухе. За 10 мин его амплитуда уменьшилась в 2 раза. Определить логарифмический декремент затухания.

5.18. Грузик массой m, подвешенный к пружине жесткостью k, колеблется в среде. Логарифмический декремент затухания равен 9. За какой промежуток времени амплитуда уменьшится в 2 раза? Сколько полных колебаний совершит тело за это время?

5.19. Два последовательных максимальных отклонения математического маятника длиной lот вертикали равны φ₁ и φ₂, φ₂ <φ₁ << 1. Вычислить логарифмический декремент затухания и период колебаний маятника.

5.20. Кусок мяса положили на весы. Три последовательных крайних положения стрелки весов были такие: a₁ = 560 г, a₂ = 440 г, a₃ = 520 г. Какова действительная масса куска мяса? Вычислить лога­рифмический декремент затухания колебаний стрелки весов.

5.21. Под действием вынуждающей силы F_x = F₀cos(ωt) груз массой m, подвешенный на пружине жесткостью k, колеблется. Определить частоту вынуждающей силы, при которой наступит резонанс.

5.22. Чему равна резонансная амплитуда у системы без трения? Имеет ли максимум резонансная кривая при коэффициенте затухания, рав­ном β ≥ ω₀ / ?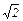

5.23. Для трех коэффициентов затухания β₁ < β₂ < β₃ нарисовать на одном чертеже качественные резонансные кривые.

5.24. Уравнение движения системы имеет вид 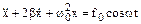. Вычислить период колебаний системы: 1) если нет вынуждающей силы и нет силы трения; 2) если система совершает установившиеся вынужденные колебания.

5.25. В молекуле азота частота колебаний атомов равна 4,45×10¹⁴ Гц, масса одного атома 2,32×10^{-26 кг. Найти коэффициент квазиупругой силы, действующей между атомами.}

5.26. Определить период, частоту и начальную фазу свободных колебаний, заданных уравнением х = Asinω(t + τ), где ω = 2,5 πс^-1, τ = 0,4 с, А - константа.

5.27. Колебания материальной точки заданы уравнением х = Acos(ωt + φ), где А = 2 см, ω = π с^-1, φ = π/4 рад. Построить графики зависимости смещения точки от положения равновесия, ее скорос­ти и ускорения.

5.28. Даны амплитуда и период свободных колебаний пружинного маятника: А = 4 см, Т = 2 с. Написать уравнение этих колебаний. В момент возникновения колебаний (0) = 0, (0) < 0.

5.29. Точка равномерно движется по окружности против часовой стрелки с периодом Т = 6 с. Диаметр окружности d = 20 см. Написать уравнение движения проекции точки на ось х. Принять, что в момент времени t = 0 х(0) = 0. Найти смещение, скорость и ускорение проекции точки в момент времени t = 1 с.

5.30. Пружинный маятник совершает гармонические колебания. Какие из приведенных выражений для полной энергии колеблющегося тела верны?

Здесь k - жесткость пружины; A - амплитуда; m - масса тела; ω - циклическая частота; x - смещение тела от положения равновесия; V - скорость; F_max - максимально упругая сила

5.31. Гармонический осциллятор совершает колебания. Какие из перечисленных величин достигают максимального значения в крайнем положении: скорость, ускорение, упругая сила, кинетическая энергия, потенциальная энергия?

5.32. Колебания материальной точки заданы уравнением
х= Acos(ωt), где А = 5 см, ω = 2 с^-1. Определить ускорение тела
в момент времени, когда скорость его будет равна 8 см/с.

5.33. Колебания математического маятника заданы уравнением φ = φ₀sin(ωt + а). Маятник отклонили на угол φ₁ = 0,1 π, а затем отпус­тили. Определить начальную фазу.

5.34. Колебания материальной точки заданы уравнением х = 7sin0,5πt. За какой промежуток времени она проходит путь от поло­жения равновесия до максимального смещения?

5.35. Записать уравнение гармонических колебаний материальной точки, если период колебаний Т = 2 с, максимальное ускорение а_max = 49,3 см/с², начальное смещение точки от положения равновесия х(0) = 25 мм.

5.36. Для гармонического осциллятора массой m с координатой х = Acos(ωt + π/4) нарисовать графики зависимостей: T(t), u(t), E(u), T(u), T(x) u(x). Т, u, E - кинетическая, потенциальная и полная меха­ническая энергия осциллятора.

5.37. Колебания гармонического осциллятора заданы уравнением х = Asin(ωt + φ₀). Выразить через амплитуду А и начальную фазу φ₀ значения координаты и скорости в момент времени t = 0.

5.38. Изобразить в моменты времени t₀ = 0 и t₁ = π /2ω на векторной диаграмме колебания: а) х = Acos(ωt + π/4), б) х = 2Acos(ωt- -π/6). Константа А > 0.

5.39. Колебания материальной точки заданы уравнением х = Acosωt, где А = 8 см, ω = 2π/3 Гц. В момент времени, когда сила, действующая на тело, в первый раз достигла 5 мН, потенциальная энергия была равна 100 мкДж. Определить этот момент времени и соответствующую ему фазу.

5.40. Частота затухающих колебаний 10³ Гц. Определить частоту собственных колебаний системы, если резонанс наблюдается при частоте 998 Гц.

5.41. Пружинный маятник массой m и с жесткостью k колеблется под действием вынуждающей силы F = F₀sin(ωt). Зависит ли амплитуда колеба­ний и как она зависит от F₀, ω, m и k? Если зависит, то каким образом?

5.42. Колебания материальной точки заданы уравнением x = Asin(ωt). В момент времени, когда смещение тела было x₁ =2,4 см его скорость достигла V₁ = 3 см/с. В момент времени, когда смещение было x₂ = 2,8 см, его скорость стала равной V₂ = 2 см/с. Найти амплитуду и период этих колебаний.

5.43. Смещение шарика массой m = 10 г от положения равновесия описывается уравнением х = Asin(πt/5 + π/4), где А = 5 см. Определить максимальную силу, действующую на тело, и его полную энергию.

5.44. Записать уравнение гармонических колебаний. Известно, что максимальная скорость материальной точки равна V_max = 10 cм/с, а ее максимальное ускорение a_max = 100 см/с². Принять начальную фазу колебаний равной нулю.

5.45. Записать уравнение гармонических колебаний материальной точки. Известно, что ее максимальное смещение x_max = 10 см, а максимальная скорость V_mах = 20 см/c. Принять начальную фазу колебаний равной нулю.

5.46. Колебания гармонического осциллятора описываются уравнением x = Asin(ωt). В некоторый момент времени смещение осциллятора х₁ было равным 5 см. Когда фаза колебаний увеличилась в 2раза, смещение стало х₂ = 8см. Определить амплитуду колебаний.

5.47. Колебания гармонического осциллятора описываются уравнением x = Asin(ωt), где А = 10 см, ω = 5 Гц. Вычислить действующую на осциллятор силу: 1) когда ωt = π/3; 2) когда смещение осциллятора максимально.

5.48. Амплитуды вынужденных колебаний при частотах вынуждающей силы n₁ = 200 Гц и n₂ = 300 Гц равны. Определить частоту, соответст­вующую резонансу.

5.49. Три последовательных аиплитудных положения качающейся стрелки гальванометра соответствуют делениям шкалы: n₁ = 20,0; n₂ = 5,6 и n₃ = 12,8. Считая декремент затухания постоянным, определить деление, соответствующее положению равновесия стрелки.

5.50. Каков общий путь, пройденный материальной точкой до полного затухания колебаний? Амплитуда первого колебания равна 1 мм, логарифмический декремент затухания равен 0,002.

КОНТРОЛЬНАЯ РАБОТА №I

Варианты заданий для студентов заочной формы обучения

Вариант Номера задач

0 1.11 1.27 2.11 2.26 3.11 3.37 4.11 4.36 5.1 5.26 1 1.12 1.28 2.12 2.27 3.12 3.38 4.12 4.37 5.2 5.27 2 1.13 1.29 2.13 2.28 3.13 3.39 4.13 4.38 5.3 5.28 3 1.14 1.30 2.14 2.29 3.14 3.40 4.14 4.39 5.4 5.29 4 1.15 1.32 2.15 2.30 3.15 3.41 4.15 4.40 5.5 5.30 5 1.16 1.33 2.16 2.31 3.16 3.42 4.16 4.41 5.6 5.31 6 1.17 1.38 2.17 2.32 3.17 3.43 4.17 4.42 5.7 5.32 7 1.18 1.39 2.18 2.33 3.18 3.44 4.18 4.43 5.8 5.33 8 1.19 1.40 2.19 2.34 3.19 3.45 4.19 4.44 5.9 5.34 9 1.20 1.41 2.20 2.35 3.20 3.46 4.20 4.45 5.10 5.35

 

Библиографический список

 

1. Волькенштейн В.С. Сборник задач по общему курсу физики. - М.: Наука, 1979.

2. Детлаф А.А., Яворский Б.М. Курс физики. - М: Высш. шк., 1989.

3. Джанколи Д. Физика. – М.:Мир, 1989.

4. Зисман Г.А., Тодес О.М. Курс общей физики. – Киев: «Днипро», 1994.

5. Иродов И.Е. Задачи по общей физике. - М.: Наука, 1988.

6. Савельев И.В. Курс общей физики. Т.1. Механика. - М.: Наука, 1989.

7. Сивухин Д.В. Общий курс физики. Т.1. Механика. - М.: Наука, 1989.

8. Стрелков С.П. Механика. - М.: Наука, 1975.

9. Трофимова Т.И. Курс физики. Учеб. пособие для вузов. - М.: Высш. шк., 1989.

10. Фиргант Е.Г. Руководство к решению задач по курсу общей физики. - М.: Высш. шк., 1978.

11. Чертов А.Г., Воробьев А.А. Задачник по физике. - М.: Высш. шк. 1981.

12. Яворский Б.М., Детлаф А.А. Справочник по физике. - М.: Наука, 1980.