Завдання: 1) Відокремити корені аналітично і уточнити один з них методом поділу відрізка навпіл;
2) Відокремити корені графічно і уточнити один з них методом поділу відрізка навпіл.
№1 1) 2х+5х-3=0,
3х4+4х3-12х2-5=0;
2) 0,5х+1=(х-2)2,
(х-3)cosx=1, -2π≤x≤2 π;
№2 1) arctgx-1/3x3=0,
2х3-9х2-60x+1=0;
2) log2(-x)(x+2)=-1
sin(x+π/3)-0,5x=0;
№3 1) 5х+3х=0,
х4-х-1=0;
2) х2-2+0,5х=0,
(х-1)2lg(х+11)=1;
№4 1) 2ex=5х+2,
2х4-х2-10=0;
2) хlog3(x+1)=1,
cos(x+0,5)= x3;
tgx=x+1; π/2≤x≤ π /2;
№5 1) 3х-1-2-х=0,
3х4+8х3+6х2-10=0;
2) (х-2)2log0,5(x-3)=-1
5sinx=x;
№6 1) arctgx-1/3x3=0,
х4-18x2+6=0;
2) x22х=1;
tg(x+1)=1, π /2≤x≤ π /2;
№7 1) e-2x-2х+1=0,
х4+4х3-8х2-17=0;
2) 0,5х-1=(х+2)2,
x2cos2x=-1;
№8 1) 5х-6х-3=0,
х4-х3-2x2+3x-3=0;
2) x2-0,5х-3=0;
хlg(х+1)=1;
№9 1) arctg(x-1)+2х=0,
3х4+4х3-12х2+1=0;
2) (х-2)22x=1,
x2 -20sinx=0;
№10 1) 2arcctgx-x+3=0,
3х4-8х3-18х2+2=0;
2) 2sin(x+ π/3)=o,5x2-1,
2lgх-x/2+1=0;
№11 1) 3х+2х-2=0,
2х4-8х3+8х2-1=0;
2) [(х-2)2-1] 2х =1
(х-2)cosx=1, -2 π ≤x≤2 π;
№12 1) 2arcctgx-3x+2=0,
2х4+8х3+8х2-1=0;
2) [log2(x+2)](x-1)=1,
sin(x-0,5)-x+0,8=0;
№13 1) 3х+2х-5=0,
х4-4х3-8x2+1=0;
2) х2-3+0,5х=0,
(х-1)2lg(х+11)=1;
№14 1) 2ex+3х+1=0,
3х4+4х3-12x2-5=0;
2) хlog3(х+1)=2;
cos(x+0,3)= x2;
№15 1) 3х-1-4-х=0,
2х3-9х2-60x+1=0;
2) (х-3)2log0,5(x-2)=-1
5sinx=x;
№16 1) arctgx-1/3x3=0,
х4-х-1=0;
2) (х-1)22x=1,
tg3x=x-1;
№17 1) ex+х+1=0,
2х4-х2-10=0;
2) 0,5х-3=(х+2)2,
х2cos2x=-1, -2 π ≤x≤2 π;
№18 1) 3х-2х+5=0,
3х4+8х3+6x2-10=0;
2) 2х2-0,5х-2=0,
хlg(х+1)=1;
№19 1) arctg(x-1)+3х-2=0,
х4-18х+6=0;
2) (х-1)22x=1,
x2 -20sinx=0;
№20 1) 2arcctgx-х+3=0,
х4+4х3-8x2-17=0;
2) 2sin(x+ π/ 3)=x2- 0,5,
2lgx-x/2+1=0;
№21 1) 2х-3х-2=0,
х4-х3-2х2+3x-3=0;
2) 0,5х+1=(х-2)2,
(х-3)cosx=1, -2 π ≤x≤2 π;
№22 1) arcctgx+2x-1=0,
3х4+4х3-12x2+1=0;
2) (x+2)log2(x)=1,
sin(x+1)=0,5x;
№23 1) 3х+2х-3=0,
3х4-8х3-18х2+2=0;
2) х2-4+0,5х=0,
(х-1)2lg(х+11)=1;
№24 1) 2ex-2х-3=0,
3х4+4х3-12x2-5=0;
2) xlog3(x+1)=1,
cos(x+0,5)= x3;
№25 1) 3х+2+х=0,
2х3-9х2-60x+1=0;
2) (х-4)2log0,5(x-3)=-1
5sinx=x-0,5;
№26 1) arctg(x-1)+2x-3=0,
х4-x-1=0;
2) (x-1)22х=1;
tg3x=x+1, π /2≤x≤ π /2;
№27 1) e-2x-2х+1=0,
2х4-х2-10=0;
2) 0,5х-3=-(х+1)2,
x2cos2x=-1, -2 π ≤x≤2 π;
№28 1) 3х-2х-5=0,
3х4+8х3+6x2-10=0;
2) 2x2-0,5х-3=0;
хlg(х+1)=1;
№29 1) arctg(x-1)+2х=0,
х4-18x2+6=0;
2) (х-1)22x=1,
х2-10sinx=0;
№30 1) 3х+5х-2=0,
3х4+4х3-12х2+1=0;
2) 0,5х+1=(x-2)2;
(х+3)cosx=1, -2 π ≤x≤2 π;
№31 1) e-2x-2х+1=0,
х4+4х3-8х2-17=0;
2) 0,5х-1=(х+2)2,
x2cos2x=-1;
№32 1) 5х-6х-3=0,
х4-х3-2x2+3x-3=0;
2) x2-0,5х-3=0;
хlg(х+1)=1;
№33 1) 3х+2х-5=0,
х4-4х3-8x2+1=0;
2) х2-3+0,5х=0,
(х-1)2lg(х+11)=1;
№34 1) 2ex+3х+1=0,
3х4+4х3-12x2-5=0;
2) хlog3(х+1)=2;
cos(x+0,3)= x2;
№35 1) 3х+2х-2=0,
2х4-8х3+8х2-1=0;
2) [(х-2)2-1] 2х =1
(х-2)cosx=1, -2 π ≤x≤2 π;
№36 1) 2arcctgx-3x+2=0,
2х4+8х3+8х2-1=0;
2) [log2(x+2)](x-1)=1,
sin(x-0,5)-x+0,8=0;
Зразок виконання завдання
1) Відокремити корені аналітично і уточнити методом спроб(поділом відрізка пополам):
x4-x3-2x2+3x-3=0
Покладемо f(x)=x4-x3-2x2+3x-3, маємо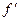 
(x)=4x3-3x2-4x+3. Знайдемо критичні точки, для того щоб з’ясувати проміжки монотонності:
4x3-3x2-4x+3=0, 4x(x2-1)-3(x2-1)=0, (x2-1)(4x-3)=0,
x1=1, x2=-1, x3=3/4;
Складемо таблицю знаків функції:
| X | -∞ | -1 | 3/4 | +∞ | |
| Signf(x) | + | - | - | - | + |
Із таблиці видно, що рівняння має два дійсні корені:
x1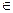 
(-∞;-1], x2 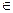[1, +∞).
Зменшимо проміжки на яких знаходиться корені:
| X | -2 | -1 | ||
| Sign f (x) | + | - | - | + |
Звідси випливає, що x1 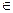[-2;-1], x2 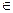[1, 2].
Уточнимо один з коренів, наприклад x1 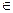[-2;-1] методом дихотомії з точністю до сотень частин. Всі обрахунки зручно проводити використовуючи таку таблицю:
| n | an | bn | xn=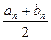 
| x4n | -x3n | -2x2n | 3xn | F(xn) |
| -2 | -1 | -1,5 | 5,0625 | 3,375 | -4,5 | -4,5 | -3,5625 | |
| -2 | -1,5 | -1,75 | 9,3789 | 5,3594 | -6,125 | -5,25 | 0,3633 | |
| -1,75 | -1,5 | -1,63 | 7,0591 | 4,3307 | -5,3138 | -4,89 | -1,8140 | |
| -1,75 | -1,63 | -1,69 | 8,1573 | 4,8262 | -5,7122 | -5,07 | -0,7981 | |
| -1,75 | -1,69 | -1,72 | 8,7521 | 5,0884 | -5,9168 | -5,16 | -0,2363 | |
| -1,75 | -1,72 | -1,73 | 8,9575 | 5,1777 | -5,9858 | -5,19 | -0,0406 | |
| -1,75 | -1,73 | -1,74 | 9,1664 | 5,2680 | -6,0552 | -5,22 | 0,1592 | |
| -1,74 | -1,73 |
x1≈-1,73
2) Відокремити корені графічно і уточнити методом спроб(поділом відрізка пополам): x2log0,5(x+1)=1
Перепишемо рівняння у вигляді log0,5(x +1)=1/ x 2, позначимо у 1=log0,5(x +1), у 2=1/ x 2 і побудуємо графіки даних функцій:
Рис. 8.2
Із рівняння видно, що рівняння має єдиний корінь x≈-0,8. Для уточнення кореня методом дихотомії виберемо проміжок, на кінцях якого функція має різні знаки f(x)=x2log0,5(x+1)-1. Складемо таблицю:
| x | -0,5 | -0,8 |
| Sign f (x) | - | + |
Підрахуємо кількість ітерацій, необхідних для уточнення кореня з точністю до ε=0,01.
.
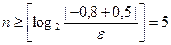Для здійснення ітерацій використаємо табличний процесор Ms Excel. Для цього у комірку А2 введемо значення лівого кінця інтервалу уточнення кореня, у А3 – правого. У комірки В2:В3 введемо значення функції. Як видно з малюнка 8.3, значення функції на кінцях інтервалу різних знаків. Щоб поділити зазначений інтервал навпіл, між рядками 2 та 3 вставимо порожній рядок. В комірку А3 введемо значення =(А4+А2)/2 та скопіюємо формулу із комірки В2 в комірку В3 (дивись Рис. 8.4).
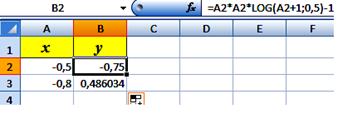
Рис. 8.3.
Рис. 8.4. Рис. 8.5.
Як видно із рисунка 8.4, на інтервалі [-0,65; -0,8] значення функції різних знаків. Вставимо порожній рядок між 3 та 4 рядком і повторимо аналогічну процедуру (Рис. 8.5). Далі поділимо навпіл інтервал [-0,725; -0,8]. Кожного разу необхідно ділити навпіл той інтервал, на кінцях якого функція приймає значення різних знаків. Після п’яти ітерацій отримуємо приблизне значення кореня x ≈-0,73
Рис. 8.6.
