Операции над числовыми величинами
| символ | Выполняемое действие |
| + | Покомпонентное (поэлементное) сложение числовых массивов одинаковой размерности; добавление скалярной величины к каждому элементу массива |
| - | Покомпонентное (поэлементное) вычитание числовых массивов одинаковой размерности; вычитание скалярной величины от каждого элемента массива |
| * | Умножение матриц в соответствии с правилами линейной алгебры; умножение всех элементов массива на скаляр |
| .* | Покомпонентное умножение элементов массивов одинаковой размерности |
| / | Деление скаляра на скаляр; покомпонентное деление всех элементов массива на скаляр; A/B=A*B  (A, B – квадратные матрицы одного порядка
|
| \ | A\B=A *B (левое матричное деление, А – квадратная матрица)
|
| .\ | A. \В - покомпонентное деление элементов массивов одинаковой размерности |
| ^ | Возведение скаляра в любую степень; вычисление целой степени квадратной матрицы |
| .^ | Покомпонентное возведение в степень элементов массива |
| ‘ | Вычисление сопряженной матрицы |
| .’ | Транспонирование матрицы |
Приоритет операций.
Логические операции (кроме операции «Логическое НЕ», называемой также операцией отрицания) имеют самый низкий приоритет. Сведения о приоритете операций (в порядке убывания) приведены ниже:
1. Круглые скобки (),
2. Транспонирование (. ), транспонирование с комплексным сопряжением (), возведение в степень (^), поэлементное возведение в степень (. ^),
3. Логическое отрицание (~),
4. Умножение и деление (. *,./,.\, *, /, \),
5. Сложение и вычитание(+,-),
6. Операции сечения массива(:),
7. Операции отношения (>, >=,<, <=,==, ~=),
8. Логическое И (&),
9. Логическое ИЛИ (|).
Отметим, что в одном выражении можно использовать все вышеперечисленные операции (арифметические, логические, операции сравнения), при этом последовательность выполнения операций определяется их расположением внутри выражения, их приоритетом и наличием круглых скобок (круглые скобки используются, в частности, для изменения приоритета операций в математических выражениях, причем степень вложения скобок не ограничивается.
ВЫЧИСЛЕНИЕ ОБРАТНОЙ МАТРИЦЫ И ОПРЕДЕЛИТЕЛЯ
Пусть 
– исходная квадратная матрица. Матрица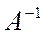 
(или 
) - обратная матрица по отношению к матрице , они связаны следующим соотношением:
,
где Е – квадратная единичная матрица такого же порядка, что и матрицы и .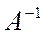
Рассмотрим простой пример.
Продемонстрируем на примере вычисление обратной матрицы методом неопределенных коэффициентов, который приводит к решению системы линейных уравнений.
Пусть исходная матрица А задана
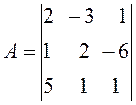
Запишем матрицу 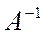в виде
и 
Умножим 1-ую строку матрицы на 1/2 и вычтем из второй строки,
умножим 1-ую строку матрицы на 5/2 и вычтем из третьей строки,
в результате получим
Умножим 2-ую строку матрицы на 17/7 и вычтем из третьей строки, в результате получим
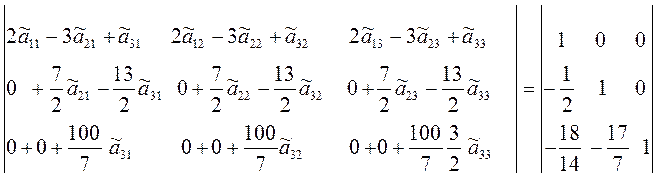
Определитель матрицы
Матрицы равны, если равны их соответствующие элементы. Приравняем их и найдем все элементы обратной матрицы.
Приравняем элементы первых столбцов:
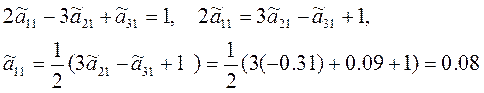
Аналогичным образом, приравнивая элементы второго и третьего столбцов, найдем
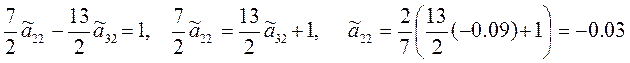
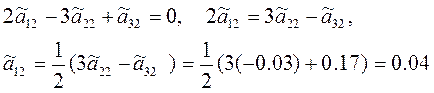
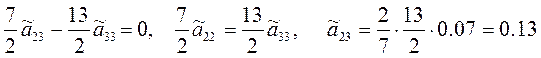
Ответ:
det=100
Более короткая форма записи вычисления обратной матрицы
Исходная матрица Расширенная матрица
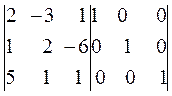
Прямой ход
1-й шаг
2-й шаг
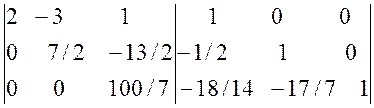
Определитель системы 
Вычисление элементов 1-го столбца обратной матрицы
из 3-го уравнения: 
из 2-го уравнения: 
из 1-го уравнения: 
Вычисление элементов 2-го столбца обратной матрицы
из 3-го уравнения: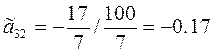 
из 2-го уравнения: 
из 1-го уравнения: 
Вычисление элементов 3-го столбца обратной матрицы
из 3-го уравнения: 
из 2-го уравнения: 
из 1-го уравнения: 
Ответ:
det=100
Вычисление обратной матрицы в системе MATLAB
1)
A=[2 -3 1; 1 2 -6; 5 1 1]
A_INV=inv(A)
2)
A=[2 -3 1; 1 2 -6; 5 1 1];
disp(‘Исходная матрица А’)
fprintf(‘\n’)
for i=1:3
fprintf(‘%8.2f’,A(i,:));
fprintf(‘\n’)
end
A_INV=inv(A)
disp(‘Обратная матрица А_INV’)
fprintf(‘\n’)
for i=1:3
fprintf(‘%8.2f’,A_INV(i,:));
fprintf(‘\n’)
end
d=det(A);
fprintf (‘det A=%8.2f’,d)
