
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе
по дисциплине «Теоретическая механика»

Выполнил студент группы ЭЛб-12-1 ________ _ Д.А. Назаренко
шифр подпись И.О. Фамилия
Нормоконтроль ____________ Л.И. Татарникова
подпись И.О. Фамилия
Курсовая работа защищена с оценкой _____________
Иркутск 2013
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
Иркутский Государственный Технический Университет
Кафедра Управления качеством и механики
ЗАДАНИЕ
на курсовую работу
По дисциплине Теоретическая механика
Студенту группы ___ Назаренко Дмитрий Александрович _ ЭЛб-12-1
Фамилия ИО Шифр группы
Тема работы: Исследование равновесия и движения механической системы.
Содержание задания: Провести статический, кинематический и динамический расчет механизма
Исходные данные: Вариант _ 13
(Изобразить схему механизма своего варианта и привести данные из условия)
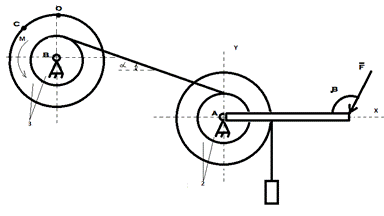
Дано: 
 м; S=0.5м;
м; S=0.5м;
 м,
м,  м
м
 м,
м,  м;
м;
 м,
м,  м;
м;
 ;
;
OC=  ;
;
где  и
и  выражены в метрах, t – в секундах.
выражены в метрах, t – в секундах.
Дата выдачи задания “ 11 ” сентября 2013г.
Дата представления работы руководителю “ 20 ” декабря 2013г.
Руководитель курсовой работы _____________ Татарникова Л.И.
Подпись ИО Фамилия
Содержание
Введение
1 Статический расчет механизма................................................................ 5
2 Кинематический расчет механизма.......................................................... 7
3 Динамический расчет механизма........................................................... 10
Заключение
Список использованных источников........................................................ 14
Введение
Теоретическая механика - наука об общих законах механического движения и взаимодействия материальных тел и механических систем.
Будучи по существу одним из разделов физики, теоретическая механика, вобрала в себя фундаментальную основу в виде аксиоматики, выделилась в самостоятельную науку и получила широкое развитие благодаря своим обширным и важным приложениям в естествознании и технике, одной из основ которой она является.
Теоретическая механика является одной из важнейших фундаментальных общенаучных дисциплин. Она играет существенную роль в подготовке инженеров любых специальностей. Теоретическая механика широко применяется в технике (авиации, космонавтике, машиностроении, кибернетике и т.д.). На базе теоретической механики возникли и успешно развиваются многие науки, такие, как сопротивление материалов, теория упругости, гидродинамика, газовая динамика и др.
Основной задачей теоретической механики является изучение движения материальных тел под действием сил. Важной частной задачей представляется изучение равновесия тел под действием сил.
 Рисунок 1 – Исследуемый механизм
Рисунок 1 – Исследуемый механизм
Решение
I. Статический расчет.
 Рассмотрим равновесие механической системы, состоящей из груза 1 и блоков 2 и 3, соединенных нерастяжимыми невесомыми тросами. На систему действуют активные силы:
Рассмотрим равновесие механической системы, состоящей из груза 1 и блоков 2 и 3, соединенных нерастяжимыми невесомыми тросами. На систему действуют активные силы:  , силы тяжести
, силы тяжести 

 пара сил с моментом М. Внешними связями, наложенными на систему, являются груз неподвижные цилиндрические шарниры А и В. Действие связей заменим их реакциями:
пара сил с моментом М. Внешними связями, наложенными на систему, являются груз неподвижные цилиндрические шарниры А и В. Действие связей заменим их реакциями: 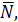
 ;
;  ,
,  .
.

Рисунок 2 –Равновесие груза 1
Внутренними связями являются тросы. Для определения реакции всех внешних и внутренних связей проводим сечения по тросам и рассматриваем отдельно равновесие груза 1, блока 2 и блока 3.
Для груза 1 (рис. 2). Силы 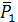 ,
,  и реакция троса
и реакция троса  образуют систему сходящихся сил на плоскости. Составим для нее уравнение равновесия:
образуют систему сходящихся сил на плоскости. Составим для нее уравнение равновесия:
 =0;
=0; 
Из него:
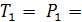 20 H
20 H
Рассмотрим равновесие блока 2 вместе с рычагом АК. Изображаем их с учетом заданных значений углов  ,
,  (рис. 3). Силы
(рис. 3). Силы  реакции
реакции 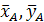 шарнира А и реакции тросов
шарнира А и реакции тросов  образуют произвольную плоскую систему сил.
образуют произвольную плоскую систему сил.

Рисунок 3 – Равновесие блока 2
Составим три уравнения равновесия:
 ;
; 
 0 (1)
0 (1)
 ;
;  0 (2)
0 (2)

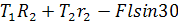 =0 (3)
=0 (3)
Вычислим неизвестные:
из(3):  =46,6H
=46,6H
из(1):
 =
= 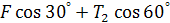 =30×0.866+46.6×0.5 =49,28H
=30×0.866+46.6×0.5 =49,28H
из(2):
 =
=  +
+  +
+  =40+20+30×0.5-46.6×0.866=34,6 H
=40+20+30×0.5-46.6×0.866=34,6 H
Рассмотрим равновесие блока 3 (рис.4).

Рисунок 4 – Равновесие блока 3
Сила тяжести  , пара сил с моментом М, реакции
, пара сил с моментом М, реакции  шарнира В и реакции
шарнира В и реакции  троса образуют произвольную плоскую систему сил. Составим три уравнения равновесия:
троса образуют произвольную плоскую систему сил. Составим три уравнения равновесия:
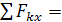 0;
0;  0 (4)
0 (4)
 0;
0; 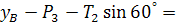 0 (5)
0 (5)
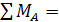 0;
0;  0 (6)
0 (6)
из (5): 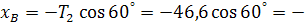 23,3 Н
23,3 Н
из (4): 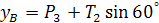 = 20+46,6
= 20+46,6  =60,35 Н
=60,35 Н
из (6): М= 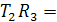 46,6
46,6  0,5=9,32 Н
0,5=9,32 Н
Знак (+) показывает, что истинное направление момента совпадает с указанным на схеме.
II. Кинематический расчет
1. Определение скорости и ускорения груза 1.
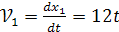
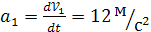
при 

2. Определение угловых скоростей и угловых ускорений блоков 2 и 3.


Исходя из схемы механизма:


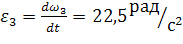
При  получим численные значения
получим численные значения
 ;
; 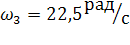
3. Определение скорости и ускорения точки С (рис. 5).






Рисунок 5 – Скорость и ускорение точки С
4. Вычисление абсолютной скорости и абсолютного ускорения точки С
(рис. 6).
При дополнительном перемещении по участку ОС движение точки С будет сложным. Ее перемещение относительно блока 3 по закону ОС= 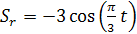 будет относительным, а вращение вместе с блоком относительно неподвижной оси переносным. Определим положение точки С на траектории относительного движения для заданного момента времени. Оно определяется углом
будет относительным, а вращение вместе с блоком относительно неподвижной оси переносным. Определим положение точки С на траектории относительного движения для заданного момента времени. Оно определяется углом
 при
при 

Для этого положения точки С определяем абсолютную скорость и абсолютное ускорение.
Абсолютная скорость точки в сложном движении находится как геометрическая сумма относительной и переносной скоростей.


Рисунок 6 – Абсолютная скорость и абсолютное ускорение точки С
Относительная скорость 
При 
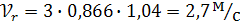
Переносная скорость 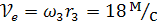
Так как векторы  и
и  лежат на одной прямой, то
лежат на одной прямой, то 
Учитывая, что переносное движение является вращательным, определим абсолютное ускорение точки С как геометрическую сумму относительного, переносного и кориолисова ускорений
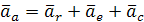 или в развернутом виде
или в развернутом виде

Относительное касательное ускорение

при  :
: 
Вектор  направлен
направлен  в сторону возрастания дуговой координаты
в сторону возрастания дуговой координаты
Относительное нормальное ускорение

Переносное касательное ускорение

Вектор  и направлен в сторону
и направлен в сторону 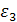
Переносное нормальное ускорение

Векторы  и
и 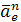 направлен к центру В
направлен к центру В
Модуль ускорения Кориолиса

Направление ускорения Кориолиса найдем по правилу Жуковского: так как вектор  уже перпендикулярен оси вращения, то повернув его на
уже перпендикулярен оси вращения, то повернув его на 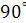 в сторону вращения, получим направление вектора
в сторону вращения, получим направление вектора 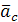 .
.
Модуль абсолютного ускорения
 =
=  =
=  =549,5
=549,5 
III. Динамический расчет
1. Вычисление кинетической энергии системы (рис. 1).
Учитывая, что груз 1 движется поступательно, а блоки 2 и 3 вращаются вокруг неподвижных осей, получим

Блоки 2 и 3 неоднородные, заданы их радиусы инерции  и
и  . Тогда моменты инерции блоков
. Тогда моменты инерции блоков  ;
; 
Кинетическая энергия системы

Подставим, все заданные величины и значения скоростей из кинематического расчета, получим 
2. Вычисление работы сил при том перемещении системы, когда груз 1 опуститься на  м (рис. 1).
м (рис. 1).
Работа сил тяжести груза 1

Работу силы  находим как работу момента, создаваемого силой
находим как работу момента, создаваемого силой
 , где угол поворота блока 2
, где угол поворота блока 2 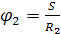
Работа момента М
 , где
, где 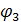 - угол поворота блока 3.
- угол поворота блока 3.
Зависимости между углами поворотов блоков такие же, как и между соответствующими угловыми скоростями  .
.
Работа остальных сил равна нулю, так как они приложены к неподвижным точкам.
Сумма работ всех сил

Поставим все заданные величины и значение момента  из статического расчета, получим
из статического расчета, получим
 =
= 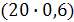 +
+  +
+  = 24,86Дж
= 24,86Дж
3. Составление общего уравнение динамики и вычисление ускорения груза 1 (рис. 7).
Общее уравнение динамики 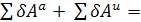 0
0
Зададим системе возможное перемещение, при котором груз 1 опуститься на  Тогда блок 2 повернется на угол
Тогда блок 2 повернется на угол  , а блок 3 повернется на угол
, а блок 3 повернется на угол
 . Груз 1 при этом получит ускорение
. Груз 1 при этом получит ускорение 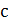 .
.
Угловое ускорение блоков 2 и 3
 ,
, 
Силы инерции груза 1 приводятся к силе  направленной противоположно
направленной противоположно 
Силы инерции блоков 2 и 3 приводится к парам, моменты которых
 ,
, 
и направлены противоположно соответствующим угловым ускорениям.
Составим сумму работ всех активных сил и сил инерции системы на возможном перемещении
 -
-  -
-  -
- 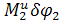 -
- 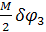 -
-  = 0
= 0
Подставим все полученные выше выражения и учтем, что 
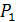 -
-  -
-  -
-  -
-  -
-  = 0
= 0
отсюда
 =
= 
Подставив все значения, находим


Рисунок 7 – Механизм под действием внешних сил
Заключение
В данной курсовой работе мы применили навыки теоретической механики при исследовании механизма. Для механизма, изображенного на рисунке 1, провели статический, кинематический и динамический расчет.
В статическом расчете определили величину и направление момента М, при которых исследуемый механизм сохраняет состояние равновесия, также были найдены реакции всех внешних и внутренних связей в положении равновесия механизма.
В кинематическом расчете определили: скорость и ускорение груза 1; угловые ускорения и угловые скорости блоков 2 и 3; скорость и ускорение точки С; абсолютную скорость и абсолютное ускорение точки С.
В динамическом расчете определили: кинематическую энергию механизма; работу всех сил. Составили общее уравнение динамики и вычислили ускорение груза 1.






