Погрешности косвенных измерений

Лекция №8

Обработка результатов измерений

Прямые однократные и многократные измерения.

1. Прямые однократные измерения.

В общем случае задача оценки погрешности полученного результата обычно осуществляется на основе сведений о пределе допускаемой основной погрешности средства измерения (по нормативно-технической документации на используемые средства измерений) и известным значениям дополнительных погрешностей от воздействия влияющих величин. Максимальное значение суммарной погрешности результата измерения (без учета знака) можно найти суммированием составляющих по абсолютной величине:

 

 

Более реальную оценку погрешности можно получить статистическим сложением составляющих погрешности:

где - граница i-й неисключенной составляющей систематической погрешности; k - коэффициент, определяемый принятой доверительной вероятностью (при Р = 0,95, коэффициент k =1,11); m - число не исключённых составляющих.

Результат измерения записывается по первой форме записи результатов:

где 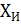- результат однократного измерения; - суммарная погрешность результата измерений; Р - доверительная вероятность (при Р = 0,95 может не указываться).

При проведении измерений в нормальных условиях можно считать

2. Прямые многократные измерения.

Точно оценить действительное значение измеряемой величины можно лишь путем ее многократных измерений и соответствующей обработки их результатов. Правильно обработать полученные результаты наблюдений – значит получить наиболее точную оценку действительного значения измеряемой величины и доверительного интервала, в котором находится ее истинное значение.

В процессе обработки результатов наблюдений необходимо последовательно решить следующие основные задачи:

- определить точечные и интегральные оценки закона распределения результатов измерений по формулам:

,

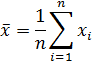
где D(x) – точечная оценка дисперсии;

- исключить «промахи» (по одному из критериев);

- устранить систематические погрешности измерений;

- определить доверительные границы не исключённого остатка систематической составляющей, случайной составляющей и общей погрешности результата измерения;

- записать результат измерения.

Оценивание погрешности косвенных измерений. Основные принципы и этапы расчетов. ГОСТы на обработку результатов.

Погрешности косвенных измерений

Оценка погрешностей, возникающих при косвенных измерениях, основывается на следующих предположениях:

1. Относительные погрешности величин, полученных прямыми измерениями и участвующих в расчете искомой величины, должны быть малы по сравнению с единицей (на практике они не должны превышать 10%).

2. Для погрешностей всех величин, участвующих в расчете, принята одна и та же доверительная вероятность. Эту же доверительную вероятность будет иметь и погрешность искомой величины.

3. Наиболее вероятное значение искомой величины получается, если для ее расчета используются наиболее вероятные значения исходных величин, т.е. их средние арифметические значения.

Погрешность в случае одной исходной величины.

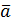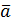Абсолютная погрешность. Пусть искомая величина y, измеряемая косвенно, зависит только от одной величины a, полученной прямым измерением. Границы интервала, в котором с заданной вероятностью лежит величина a, определяются средним арифметическим значением и полной абсолютной погрешностью a величины a. Это значит, что значение a может лежать внутри интервала с границами ± a.

При косвенном измерении для величины y (a) такие границы будут определяться ее наиболее вероятным значением = y (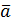) и погрешностью y, т.е. значения y лежат внутри интервала с границами ± y. Верхней границей для y (при монотонном возрастании) будет значение, соответствующее верхней границе a, т.е. значение + y = y ( + а). Таким образом, абсолютная погрешность y величины y имеет вид приращения функции y(a), вызванного приращением ее аргумента a на величину a его абсолютной погрешности. Следовательно, можно воспользоваться правилами дифференциального исчисления, согласно которому при малых значениях a приращение y можно приближенно выразить в виде

 

(1)

 

Здесь - производная по a функции y(a) при a = .

Таким образом, абсолютная погрешность окончательного результата может быть вычислена с помощью формулы (1), причем доверительная вероятность соответствует той доверительной вероятности, которую имеет a.

Относительная погрешность. Чтобы найти относительную погрешность значения y, поделим (1) на y и примем во внимание, что

 

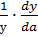
представляет собой производную по a натурального логарифма y. В результате получится

 

 

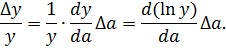
Если в это выражение подставить a = 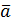и y = , то его значение и будет относительной погрешностью величины y.

Для обработки результатов измерений используется ГОСТ 8.207-76 «ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений».

8.3. Результат измерения и оценка его среднего квадратического отклонения:

1. Способы обнаружения грубых погрешностей должны быть указаны в методике выполнения измерений. Если результаты наблюдений можно считать принадлежащими к нормальному распределению, грубые погрешности исключают.

2. За результат измерения принимают среднее арифметическое результатов наблюдений, в которые предварительно введены поправки для исключения систематических погрешностей.

3. Среднее квадратическое отклонение S результата наблюдения оценивают согласно НТД.

4. Среднее квадратическое отклонение результата измерения оценивают по формуле

 

,

где х_i - i -й результат наблюдения;

- результат измерения (среднее арифметическое исправленных результатов наблюдений);

n - число результатов наблюдений;

- оценка среднего квадратического отклонения результата измерения.

8.4. Доверительные границы случайной погрешности результата измерения:

1. Доверительные границы случайной погрешности результата измерения в соответствии с настоящим стандартом устанавливают для результатов наблюдений, принадлежащих нормальному распределению. Если это условие не выполняется, методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.

1.1. При числе результатов наблюдений n >50 для проверки принадлежности их к нормальному распределению по НТД предпочтительным является один из критериев: χ² Пирсона или ω² Мизеса - Смирнова.

1.2. При числе результатов наблюдений 50> n >15 для проверки принадлежности их к нормальному распределению предпочтительным является составной критерий.

При числе результатов наблюдений n ≤15 принадлежность их к нормальному распределению не проверяют. При этом нахождение доверительных границ случайной погрешности результата измерения по методике, предусмотренной настоящим стандартом, возможно в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению.