Лекция 4. Знакомство с итерационными методами
Для начала небольшой фокус: давайте рассмотрим следующую систему уравнений:
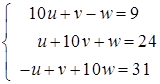(4.1)
Решением этой системы, как нетрудно убедиться, являются значения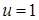 
, 
, 
. Перепишем ее, разрешив первое уравнение относительно первой неизвестной, второе относительно второй и третье относительно третьей:
(4.2)
При этом мы снабдили неизвестные, оказавшиеся слева от знака равенства, индексом 
, а справа – индексом 
. Теперь зададимся взятыми наугад начальными значениями неизвестных, например, 
. Подставим эти значения в правые части уравнений (4.2) и найдем первое приближение:
(4.3)
Следующее, второе, приближение находим, подставляя в правые части (4.2) найденные значения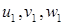 
:
(4.4)
Уже сейчас можно заметить, что с каждым приближением мы все ближе к точному решению. Выполнив еще одно приближение (вычисления здесь производятся с точностью до двух знаков после запятой), получаем полное совпадение третьего приближения с точным решением системы (4.1):
(4.5)
Этот способ решения носит название метода Якоби[1]. Возникает законный вопрос – для всякой ли системы линейных уравнений описанный итерационный процесс будет приводить к правильному решению? Для метода Якоби ответ не очень утешительный – не всегда. Однако можно сказать, что этот метод будет сходиться в случае, если диагональные элементы матрицы системы значительно больше внедиагональных.
Существенно лучше характеристики усовершенствованного варианта описанного метода, который принято называть методом Гаусса ‑ Зейделя. В методе Гаусса ‑ Зейделя исходная система точно так же приводится к виду (4.2). Так же произвольно выбираются значения «нулевого» приближения. Пусть вновь 
. Находим первое приближение первой неизвестной
. (4.6)
Пока что все идет так же, как и в методе Якоби. Однако теперь, при определении первого приближения второй неизвестной, в правую часть второго уравнения (4.2) будем подставлять не 
, а найденное только что значение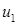 
:
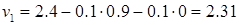. (4.7)
При определении третьей неизвестной уже используем найденные 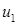и 
:
. (4.8)
Про метод Гаусса-Зейделя уже можно сказать, что он сходится для системы с симметричной положительно определенной матрицей [4.1]. Как уже отмечалось в § 3, такие матрицы особенно важны в задачах механики твердого тела. Впрочем, оба рассмотренных метода представляют скорее исторический интерес. В настоящее время предпочтение отдается, как правило, методу верхней релаксации или методу сопряженных градиентов. Эти методы сходятся для любой системы и обладают более высокой скоростью сходимости, чем методы Якоби и Гаусса-Зейделя. Прежде чем рассмотреть эти методы заметим, что все итерационные алгоритмы следуют одной схеме.
1. Для линейной системы 
определяется правило, следуя которому можно определить по значениям неизвестных -го приближения 
значения неизвестных следующего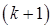 
-го приближения 
:
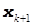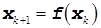. (4.9)
Это правило определяется различным образом для разных методов.
2. Задается начальное приближение неизвестных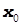 
.
3. Следуя правилу (4.9), вычисляем приближения 
до тех пор, пока очередное приближение не будет совпадать с точным решением с требуемой точностью. Обычно момент, когда можно прекратить итерации, определяется путем сравнения очередного приближения с предыдущим.
Для более серьезного ознакомления с итерационными методами решения систем линейных уравнений можно порекомендовать [4.2]. Детальное описание и обоснование итерационных алгоритмов содержится в [4.3].
Литература
4.1. Стренг Г. Линейная алгебра и ее применения. – М.: Мир, 1980. – 454с.
4.2. Хаусхолдер А.С. Основы численного анализа. – М.: ИЛ, 1956. – 320с.
4.3. Хейгеман Л., Янг Д. Прикладные итерационные методы. – М.: Мир, 1986. – 448с.
[1] Якоби Карл Густав Якоб (1804-1851) – немецкий математик. Труды по вариационному исчислению, математическому анализу, дифференциальным уравнениям, теоретической механике
