Лекция 3. Метод Холецкого
Метод Гаусса, подробно рассмотренный выше, был и остается основным инструментом для решения систем линейных уравнений. Основным, но не единственным. Нам следует получить представление еще о двух группах методов: 1) методы разложения матрицы на треугольные множители; 2) итерационные методы.
Рассмотрим метод Холецкого, который предназначен для решения систем с симметричными положительно определенными матрицами. Почему нас интересуют именно такие матрицы?
Во-первых, как известно, матрица жесткости (см (1.1)) является симметричной матрицей.
Во-вторых, вспомним, что при использовании метода конечных элементов потенциальная энергия конструкции определяется выражением
, (3.1)
где q – вектор перемещений конструкции, а K – ее матрица жесткости.
Аналогично, для кинетической энергии системы получено
, (3.2)
где M – матрица инерции.
В исходном, недеформированном, состоянии 
потенциальная энергия деформации конструкции равна нулю. В то же время любые перемещения точек конструкции приводят к ее деформации и, значит, к увеличению П по сравнению с недеформированным состоянием. Таким образом, исходя только из соображений физического смысла, мы пришли к выводу о положительной определенности матрицы жесткости. Подобные соображения можно привести и для матрицы инерции.
Теорема Холецкого. Если A – симметричная положительно определенная матрица, то существует действительная невырожденная нижняя треугольная матрица L такая, что 
, т.е.
(3.3)
Согласно этой теореме мы можем заменить в исходной системе линейных уравнений 
матрицу 
на ее разложение:
. (4)
Если мы обозначим 
, то можем легко решить задачу в два этапа:
1) 
- определяем y;
2) 
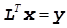- определяем x.
Обе эти системы с треугольными матрицами и, следовательно, легко решаются. То есть разложение Холецкого дает возможность заменить сложную задачу решения системы уравнений с полностью заполенной матрицей двумя простыми задачами – решение двух систем с треугольной матрицей.
Остается только научиться строить матрицу L.
Вспомним определение произведения матриц: 
. Следовательно, элемент 
есть произведение i -й строки матрицы L на j- й столбец матрицы 
:
. (3.5)
Учтем симметричность матрицы A. Это значит, что мы можем ограничиться рассмотрением только элементов нижнего треугольника матрицы A 
:
. (3.6)
Теперь для получения удобных для использования формул полезно записать это выражение отдельно для поддиагональных и для диагональных элементов матрицы A:
(3.7)
Кстати, эти формулы позволяют понять, почему в теореме Холецкого содержится ограничение, которое требует положительной определенности матрицы . Если попытаться применить формулы (3.7) к матрице, не являющейся положительно определенной, то это приведет либо к получению отрицательного числа под знаком квадратного корня при вычислении 
, либо к некорректной операции деления на ноль при вычислении 
.
Пример. Найти по схеме Холецкого решение системы:
(3.8)
Матрица этой системы
(3.9)
в результате применения формул (3.7)
представляется в виде разложения 
, где
(3.10)
Теперь находим решение исходной системы путем решения двух треугольных систем:
1) 
2) 
