Представление о многошаговых методах

Лекция 17

Одношаговые и многошаговые методы

Методы Рунге-Кутты

 

Метод Эйлера приятно радует своей простотой. Однако пример, рассмотренный в §20, наводит и на грустные размышления. Выполнив численное интегрирование уравнения за пять шагов, мы получили ответ, отличающийся от точного решения на 20%. Уменьшив шаг интегрирования вдвое, эту же задачу решили за 10 шагов и получили погрешность 10%. Между тем, даже в докомпьютерную эпоху, когда главным вычислительным средством была логарифмическая линейка, нормальной точностью инженерных расчетов считали результат с 3-4 значащими цифрами, т.е. погрешность около 0.1%. Получается, что для удовлетворительного решения даже такой простой задачи потребуется примерно 1000 шагов интегрирования.

Попробуем немного усовершенствовать метод. Вновь начнем с геометрических соображений. Пусть нам известно – значение функции при – точка 1 на рис.21.1. Проведем через эту точку касательную к искомой кривой. Направление касательной известно, поскольку определено самой решаемой задачей:

. (21.1)

Следовательно,

. (21.2)

Точка 2 пересечения касательной с вертикалью соответствует приближению Эйлера. Теперь проведем из точки 2 с координатами 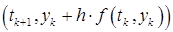прямую с аналогично (21.2) определенным угловым коэффициентом:

. (21.3)

Посмотрите еще раз на рис.21.1. Не возникло ли у вас подозрения, что если провести из точки 1 прямую не под углом 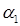, а выбрать для углового коэффициента «золотую середину»:

, (21.4)

то результат (точка 3) будет лучше, чем в методе Эйлера (точка 2)? Возможно, во всяком случае, это стоит проверить.

Итак, проверяем «улучшенный» метод Эйлера, который согласно (21.4) предлагает для приближенного решения в очередной точке следующую формулу:

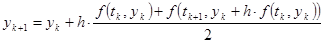. (21.5)

Для рассмотренной в § 20 задачи

(21.6)

результаты, полученные по методу (21.5), как видно из нижеследующей таблицы, совпадают с точным решением (21.6) – .

	0.0	0.00	0.0	0.00	0.2	0.01
	0.1	0.01	0.2	0.03	0.4	0.04
	0.2	0.04	0.4	0.08	0.6	0.09
	0.3	0.09	0.6	0.15	0.8	0.16
	0.4	0.16	0.8	0.24	1.0	0.25
	0.5	0.25

 

Конечно, это не означает, что метод (21.5) всегда так точен. В данном случае просто методу повезло с задачей. Метод Эйлера ‑ метод первого порядка ‑ как можно видеть из рис.20.1, заключается в замене неизвестной функции на линейную в пределах одного шага. «Улучшенный» метод Эйлера (20.5) является методом второго порядка (см, например, [17.1]). Можно показать, что формула (20.5) получена в результате аналогичной «подмены» неизвестной кривой на полином второй степени в пределах одного шага. Поскольку и искомое решение и кривая, аппроксимирующая решение, являются кривыми второго порядка, для этой конкретной задачи (20.6) значения, полученные, вообще говоря, приближенным методом, оказались точными. В общем случае полного совпадения, как правило, не бывает.

В качестве примера приведем решение обоими рассмотренными методами простого дифференциального уравнения

. (7)

		Точное решение	Метод Эйлера	«Улучшенный» метод Эйлера
	0.0	1.000	1.000	1.000
	0.1	1.105	1.100	1.105
	0.2	1.221	1.210	1.220
	0.3	1.350	1.331	1.348
	0.4	1.492	1.464	1.487
	0.5	1.649	1.611	1.641
	0.6	1.822	1.772	1.810
	0.7	2.014	1.949	1.996
	0.8	2.226	2.144	2.201
	0.9	2.460	2.358	2.426
	1.0	2.718	2.594	2.673

 

Метод Эйлера и «улучшенный» метод, который, кстати, в литературе носит название метода Хьюна, несмотря на различия имеют много общего. И тот и другой метод можно представить в виде

. (21.8)

В методе Эйлера:

. (21.9)

В методе Хьюна:

. (21.10)

Оба метода для получения очередного значения искомой функции требуют информации только об одной предыдущей точке. Такие методы называются одношаговыми или методами Рунге-Кутты. Для этих методов разработана теория, позволяющая получать с помощью формулы Тейлора методы любого порядка точности.

Использование метода высокого порядка позволяет добиться повышения точности и, следовательно, позволяет снизить необходимое число шагов интегрирования. Однако при этом усложняется вид . По-видимому, золотой серединой является наиболее знаменитый классический метод Рунге-Кутты 4-го порядка, определяемый следующими соотношениями:

(21.11)

 

 

Представление о многошаговых методах

 

Одношаговые методы никак не используют информацию о предыдущих шагах – предыстории решения. Для получения решения задачи Коши:

(22.1)

в точке используются только результаты, полученные для . Точки не используются. Не является ли такое отбрасывание информации непозволительной роскошью? Ведь житейский опыт говорит, что по поведению чего-либо (утюга, домашнего животного, жены или начальника) в прошлом, можно более-менее уверенно прогнозировать его поведение в будущем. Давайте посмотрим, что получится из попытки перевести эту житейскую мудрость на язык математики.

Проинтегрируем дифференциальное уравнение (22.1) на отрезке :

. (22.2)

Поскольку решение нам неизвестно (мы его пока только ищем), вычислить интеграл из (22.2) непосредственно мы пока не можем. Однако приближенно вычислить его можно, если заменить неизвестную подынтегральную функцию некоторым полиномом , приближенно равным этой функции на . Для того чтобы выбрать такой полином, можно и нужно использовать результаты предыдущих шагов интегрирования.

Здесь рассмотрим самый простой вариант, когда в качестве используется полином первой степени, т.е. линейная функция. Поскольку для задания прямой нужны две точки, нам потребуются значения и . Нетрудно убедиться, что линейной функцией, значения которой в точках 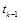и совпадают с функцией , будет

, (22.3)

где – постоянный шаг интегрирования.

Подставляя эту функцию в интеграл (22.2), получаем

(22.4)

и, следовательно,

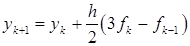. (22.5)

Выражение (22.5) описывает двухшаговый метод численного решения дифференциальных уравнений. Можно показать (см. [17.1]), что это метод второго порядка.

Используя значения 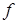в большем количестве предыдущих точек, можно получить методы более высокого порядка. Например, метод третьего порядка:

. (22.6)

Очевидно формулы для многошаговых методов попроще, чем для одношаговых методов того же порядка. Однако у многошаговых методов есть и существенный недостаток – они не могут стартовать самостоятельно. Поэтому на практике обычно используется комбинированный подход. Сначала интегрирование ведется по методу Рунге-Кутты. Затем, когда уже пройдено достаточное количество шагов интегрирования, включается многошаговый метод.

 

ЗАКЛЮЧЕНИЕ

Данное пособие нельзя считать достаточно полным для детального изучения численных методов. Так, почти полностью опущены вопросы анализа погрешностей, доказательства сходимости. При обосновании методов предпочтение часто отдавалось не строгим математическим доказательствам, а геометрическим аналогиям, рассуждениям на «пальцах».

То есть надо отдавать себе отчет, что материал данного пособия предназначен лишь для предварительного знакомства с численными методами. Впрочем, воспользовавшись приведенными здесь описаниями алгоритмов, можно составить вполне корректные и работоспособные программы. Однако если вам придется заняться такой работой, очень скоро вы обнаружите, что для повышения быстродействия, точности результатов ваших программ понадобятся более полные сведения, которые можно найти, например, в литературе из списка в конце книги.

Еще немного о том, что стоит сохранить в своей памяти учащимся и зачем им это нужно. В самом деле, даже если по окончании института вы будете работать по специальности, то для расчетов вы будете чаще всего пользоваться не своими программами, а мощными программными комплексами типа NASTRAN, ДИАНА и др. Эти комплексы уже содержат программные средства для решения рассмотренных здесь задач. Так стоит ли тратить время на изучение всех этих численных методов, если можно будет воспользоваться готовыми программами? На взгляд автора, стоит и вот почему.

Во-первых, представление об этих методах необходимо хотя бы для того, чтобы можно было грамотно выбрать подходящий метод из предлагаемых вам конкретным программным комплексом. Так, для решения задачи о собственных значениях комплекс NASTRAN предлагает семь различных методов.

Во-вторых, стандартные программы, как правило, содержат специальные параметры, позволяющие управлять режимом работы программы. Чтобы более-менее обоснованно выбрать нужные значения таких параметров, необходимо хотя бы в общих чертах представлять себе, как работает данный метод, как он «устроен внутри».

В-третьих, первая же неприятность с использованием стандартных программ может поставить вас в положение автолюбителя, с тоской взирающего на остановившуюся машину и не представляющего, как сдвинуть ее с места. Для специалиста такая роскошь недопустима.

В-четвертых, при решении конкретных задач (например, расчет колебаний некоторой типовой конструкции) могут возникать достаточно специфические задачи с матрицами вполне определенной структуры. В таких случаях кустарные программы, учитывающие специфику конкретной задачи, могут оказаться эффективней профессионально выполненных стандартных программ, рассчитанных на общий случай.

 

Литература

17.1. Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1989. – 432с.