5.1 Первый этап
Для выбора схемы необходимо представить свой номер по журналу студенческой группы в двоичной записи согласно таблице 1. Для студентов заочного обучения можно использовать вместо номера по журналу две последние цифры в номере зачетной книжки. Если этот номер превышает число 31, то берется любая цифра из двух.
Таблица 1 – Перевод десятичных чисел в двоичные числа
Далее установить переключатели К1- К5 (рисунок 1) в положения, соответствующие Вашему номеру N в двоичной записи. Пример приводится в таблице 2.
Таблица 2 – Положение ключей в схеме
| Ключи | К1 | К2 | К3 | К4 | К5 |
| Двоичная форма записи числа 12 | |||||
| Положение ключей |
Зарисуйте получившуюся схему без переключателей и отсоединенных элементов.
Определение величин элементов схемы и частоты генераторов осуществляется по формулам: (1), (2), (3), (4). Все генераторы в схеме имеют одинаковую частоту, определяемую по формуле (4).
5.2 Второй этап.
Второй этап заключается в определении тока в цепи источника Ė1, когда все остальные источники закорочены (удалены).
Здесь требуется воспользоваться формулами для последовательного и параллельного соединения нескольких элементов, вычислив эквивалентное комплексное сопротивление Zэ. Значение тока в цепи источника определяется по формуле
İ = 
= I · еjφ
и затем выражается во временной форме, т.е.
i (t) = Im · cos (ωt +φ).
По результатам расчетов строится векторная диаграмма.
5.3 Третий этап
Третий этап заключается в расчете сложной электрической цепи по схеме из п. 3.4., т.е. определении токов и напряжений на всех элементах цепи при известных значениях R, C и Ė.
Для расчета электрической схемы необходимо составить систему уравнений по методу контурных токов [ 1 ].
Вначале составляется граф электрической схемы, по которому выбираются независимые контуры и задаются контурные
токи. Для этих контуров составляются уравнения по второму закону Кирхгофа с учетом совместного влияния одного контура на другой. Направление обхода во всех контурах выбираются одинаковыми.
Знак падения напряжения в основном контуре от токов соседних контуров выбирается плюс, если их направление совпадает с основным контурным током, и минус в случае несовпадения.
По системе уравнений составляется матрица сопротивлений Z, т.е. выписываются соответствующие коэффициенты при токах İ1, İ2, …, İn.
Токи в контурах (контурные токи) определяются по формуле Крамера [ 1 ]
İn = 
(n = 1, 2, …, ℓ), (5) где 
- полный определитель матрицы сопротивлений Z;
n – определитель, получающийся из при замене его элементов к-го столбца соответствующими правыми частями уравнений.
Все расчеты необходимо производить на ЭВМ в среде, например, Mathcad 8/2000 [ 2 ] или других аналогичных версиях.
Для этой цели необходимо на экран ЭВМ вывести основное окно Mathcad. С помощью нажатия левой кнопки мыши открыть панель «Просмотр» (View) и далее указатель мыши перевести на строку «Панели» и перемещая указатель вправо установить его на надписи «Математика» и щелкнуть левой кнопкой. В появившейся панели выбрать изображение матрицы и далее в следующей появившейся панели щелкнуть кнопкой на изображении матрицы и затем выбрать необходимую ее размерность.
В появившийся трафарет матрицы следует вводить комплексные числа в виде, например 2 – 3i или действительные числа, например 10. Синий уголок ввода числа перемещается
стрелкой мыши с последующим нажатием левой кнопки или
кнопками «←↕→». После набора всех чисел следует выделить синим уголком всю матрицу. Это осуществляется путем нажатия клавиши «Пробел» или клавиши «→». Затем следует ввести в матрицу знак определителя | X | из иконки действий с матрицами и потом в иконке знаков выбрать действие «═». Значение определителя матрицы будет найдено.
Аналогично следует вычислить все определители n и воспользовавшись выражением (5) найти значения всех контурных токов İn , через которые затем определить токи во всех элементах схемы, воспользовавшись правилом, когда ток в элементе равен контурному току, если он протекает здесь один и равен алгебраической сумме контурных токов, если их несколько.
Затем следует определить эти же токи методом обращения матрицы, принимая во внимание выражение
, (6)
где 
- обратная матрица комплексных сопротивлений схемы, состоящая из коэффициентов
. (7)
Значения контурных токов İn в этом случае определяются через формулы:
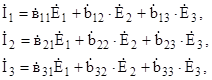(8)
Значения токов в элементах схемы находятся аналогично как и в методе Крамера.
Для вычисления следует над введенной и выделенной синим уголком матрицей 
поставить из иконки действий с матрицами знак степени «Х-1 ». Затем следует выделить синим уголком и применить знак «═» из иконки знаков. В результате будут получены коэффициенты bin из выражения (7).
Применив формулы (8) следует вычислить токи в ветвях и далее токи в элементах схемы.
Используя законы Кирхгофа проверить результаты расчетов.
5.4 Четвертый этап
Четвертый этап заключается в получении выражения (формулы) для комплексного коэффициента передачи 
схемы по п. 3.3 в соответствии с его определением
(9)
и построении графиков АЧХ и ФЧХ.
В соответствии с этим прежде всего необходимо найти выражение для 
Напряжение 
лучше всего определять используя метод контурных токов.
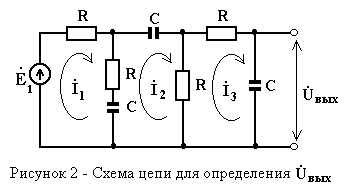
Так, например, для схемы, изображенной на рисунке 2 составим соответствующую для этого систему уравнений по методу контурных токов. Для всех вариантов значение R=1000 Ом, а С = 1 nФ = 1∙ 10-9 Ф.
Используя принятые применительно к этому методу правила, получим систему уравнений
(10)
где Zc = - j x c, x c = 
, 
= - 
, 
= j 
.
Определяя из первого уравнения İ1 и подставляя его выражение во второе уравнение, находим İ2, которое затем подставляем в третье уравнение и из него определяем выражение для İ3.
Напряжение на выходе цепи будет равно
= İ3 · Zс,
а выражение для комплексного коэффициента передачи может быть найдено в соответствии с (9).
В результате последующих преобразований необходимо сгруппировать действительные и мнимые части в числителе и знаменателе, получив, например, выражение для 
в виде
 |
. (11)
