Основные понятия, исходные соотношения и гипотезы
Рассмотрим многослойную тонкую оболочку постоянной общей толщины 
, собранную из произвольного числа однородных анизотропных слоев постоянной толщины 
( рис.2.1 ).
Предполагается, что в каждой точке каждого слоя оболочки имеется лишь одна плоскость упругой сим-метрии, параллельная координатной поверхности оболочки; координатная поверхность параллельна внешним поверхностям оболочки и проходит внутри какого-либо слоя.
Пусть 
и 
являются криволинейными ортогональными ко-ординатами, совпадающими с лини-ями главной кривизны координатной поверхности оболочки, и 
, будучи нормальной к координатным линиям 
, 
. является прямолинейной и представляет расстояние по нормали от точки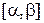 
коорди-натной поверхности до точки 
оболочки (рис.2.2). Допустим, что все слои оболочки при деформации остаются упругими, т.е. подчиняются обобщенному закону Гука и работают совместно, без скольжения.
В выбранной триортогональной системе координат для коэффициентов Ляме имеем
, 
, 
, (2.1)
где 
и 
являются коэффициентами первой квадратичной формы координатной поверхности, 
, 
– главные кривизны координатной поверхности оболочки на линиях соответственно , .
Для компонентов деформаций 
-го слоя оболочки имеем
; (2.2)
; (2.3)
; (2.4)
; (2.5)
; (2.6)
. (2.7)
Основной предпосылкой для построения теории тонких анизотропных слоистых оболочек является гипотеза недеформированных нормалей. Она формулируется так: нормальный к координатной поверхности прямолинейный элемент оболочки после деформации остается прямолинейным, нормальным к деформированной координатной поверхности оболочки и сохраняет свою длину, а также нормальными напряжениями 
на площадках, параллельных координатной поверхности тонкой оболочки, можно пренебречь по сравнению с другими напряжениями.
Принимая гипотезу недеформированных нормалей, в теории оболочек вносится погрешность, которая будет порядка 
, однако есть случаи, когда эта погрешность значительно больше.
Допуская обычную для инженерного расчета относительную погрешность 5 %, тонкими считаются такие оболочки, у которых 
и одновременно 
, где 
– минимальный линейный размер оболочки в координатной поверхности, 
– малая величина (например, для изотропной оболочки ~ 0,1). Второе условие заимствовано из теории пластин, является обязательным. Так как если тонкую оболочку определять только с точки зрения отношения толщины оболочки к минимальному радиусу кривизны координатной поверхности (первое условие), то она с точки зрения теории пластин (второе условие) может оказаться толстой, и принятое основное предположение станет неприемлемым.
Данное выше определение тонкой оболочки носит несколько условный характер, так как если толщину оболочки рассмотреть с точки зрения возможности применения гипотезы недеформируемых нормалей, то приведенное геометрическое определение тонкой оболочки в случае анизотропных слоистых оболочек будет нуждаться в существенных коррективах, о чем будет сказано ниже.
Перемещения, деформации и напряжения в слоях
Геометрическая гипотеза о деформированных нормалях, данная для всего пакета оболочки в целом, освобождает нас от необходимости рассмотрения перемещений и деформаций каждого слоя в отдельности.
Имея деформации удлинения и сдвига, а также параметры, характеризующие изменение кривизны и кручения координатной поверхности оболочки, можно определить деформации и перемещения любого слоя оболочки.
Пользуясь основной гипотезой, можно записать следующие равенства:
, 
, 
, (2.8)
или для отдельного слоя оболочки
, 
, 
, (2.9)
которые равномерны допущению о том, что деформация оболочки в целом происходит без деформаций сдвига 
, 
в плоскости нормальных сечений и без деформаций удлинения 
по толщине оболочки.
В связи с этим, имеем
, 
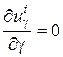, (2.10)
т.е. нормальное перемещение 
точки какого-либо слоя оболочки не зависит от координаты . Нормальные перемещения всех точек нормального элемента имеют постоянное значение и равняются нормальному перемещению 
той точки координатной поверхности, которая образуется при перемещении данной нормали с координатной поверхностью оболочки.
Для тангенциальных перемещений -го слоя оболочки имеем
; (2.11)
, (2.12)
где 
, 
тангенциальные перемещения соответствующей точки координатной поверхности оболочки.
Таким образом, формулами (2.10 – 2.12) устанавливается геометрическая модель деформированного состояния оболочки, а деформации имеют вид
; (2.13)
; (2.14)
, (2.15)
где 
– относительные деформации удлинений и сдвига координатной поверхностью оболочки;
– изменения кривизны координатной поверхностью оболочки,
– деформации сдвига, 
– относительная деформация кручения).
Пользуясь основной гипотезой, пренебрегая напряжениями из обобщенного закона Гука, получим
; (2.16)
; (2.17)
, (2.18)
где для коэффициентов 
имеем
; 
;
; 
; (2.19)
; ;
. (2.20)
