I i 53 52 53 52 53
б) Аналогично находим вероятность события B
При выполнении гипотезы Н1 во второй урне станет 22 белых и 26 черных шаров, при выполнении гипотезы Н2 – 21 белых и 27 черных шаров, поэтому условные вероятности наступления события B при выполнении гипотез равны:
P (B H) = 22,
P (B H
) =21
1 48 2 48
По формуле полной вероятности имеем:
P (B) =
n
å
i =1
P (H) P (BH) =24 ×22 +29 ×21 =1137 =379
i i 53 48 53 48 2544 848
Ответ:
P (A) = 24,
P (B) = 379
53 848
Задача 5. На I складе имеется 10+α=29 изделий, из которых 3 бракованных; на II складе находятся 15+ α=34 изделие, из которых 5 бракованных. Из каждого склада выбирается по одному изделию случайным образом. После чего из этой пары отбирается одно изделие, которое оказалось небракованным. Какова вероятность, что это изделие из I склада?
n 1 = 29 - общее количество изделий на 1 складе
a 1 = 3 - количество бракованных изделий на 1 складе
b 1 = 26 - количество стандартных изделий на 1 складе
n 2 = 34 - общее количество изделий на
2 складе
a 2 = 5 - количество бракованных изделий на
2 складе
b 2 = 29 - количество стандартных изделий на
2 складе
А - событие { изпары изделий извлечено стандартное изделие }
Найти:
P (Н 1 A)
Решение
Рассмотрим следующие возможные гипотезы:
H 1 - гипотеза H 2 - гипотеза
{изпарыизделийотобраноизделиес 1-го склада}
{ изпарыизделийотобраноизделиесо 2 - го склада }
Вероятности этих гипотез:
P (H) = 1,
P (H
) = 1
1 2 2 2
n
Проверка:
P (H) = P (H) + P (H
) = 1 + 1 = 1 (верно)
å i
i =1
1 2 2 2
Теперь найдем условные вероятности:
ìотобранное изделие стандартно,
при условии,ü
A H 1 - событие í
что оно с 1- го склада ý
î þ
ì отобранное изделие стандартно, при условии,ü
A H 2 - событие í
что оно со 2 - го склада ý
î þ
P (A H) = 26,
P (A H
) =29
1 29 2 34
По формуле полной вероятности найдем вероятность события A:
n
P (A) =
å
i =1
P (H) P (A H) = 1 × 26 + 1 × 29 = 1725
I i 2 29 2 34 1972
Вероятность извлечения из пары изделия с 1-го склада, при условии, что оно оказалось стандартным, найдём по формуле Бейеса:
Times;26
P (Н A) = = 2 29 =
» 0,51
Ответ:
P (A)
P (Н A) =
1 1725
Задача 6. Среди (3+α)=22 часов, поступивших в ремонт, 2 с поломками оси. Наудачу взяты 3 часов. Составить ряд распределения числа часов с поломками оси среди взятых трех. Найти функцию распределения дискретной случайной величины. Построить ее график.
n = 22 - общее количество часов
a = 2 - количество часов с поломками оси b = 20 - количество исправных часов
X - случайная величина числа часов с поломками оси среди взятых трех
Найти:
ряд распределения случайной величины X,
F (x) и ее график
Решение
Случайная величина X распределена по гипергеометрическому закону распределения. Здесь она может принимать значения 0, 1, 2.
Найдем соответствующие вероятности:
20!
C 0 × C 3 1×
1140 57
P (X
=0) = 2 20 = 3!17! = =
C 3 22! 1540 77
22
3!19!
20!
C 1 × C 2 2 ×
380 19
P (X
=1) = 2 20 = 2!18! = =
|
C 2 × C 1
1540 1540 77
1× 20 1
P (X = 2) = 2 20 = =
|
Составляем ряд распределения (закон распределения) случайной величины X:
| xi | 0 | 1 | 2 |
| pi | 57/77 | 19/77 | 1/77 |
Проверка:
n
å pi
= P (X = 0) + P (X = 1) + P (X = 2) = 57+ 19+ 1
= 1 (верно)
i =1
77 77 77
Функция распределения представляет собой вероятность выполнения неравенства X<x, где X – значение случайной величины, полученное в результате опыта, x – заданное
значение случайной величины X, т. е.
F (х) = P (X < х).
Поэтому 1) если x ≤ 0, то существует;
F (x) =0, т.к. значения X, меньшего заданного
x =0 не
2) если 0 < х £1, то
F (х)= F (1)= P (X <1)=57/ 77, т.к. при
х £1 X может иметь
только одно значение X =0;
3) если 1 < х £2, то X может принять случайно два значения 0 и 1.
F (х) = F (2) = P (X < 2) = 57 / 77 +19 / 77 = 76 / 77;
4) если х >2, то X может принять любое значение 0; 1; 2 поэтому
F (х)= P (X < x) =57/ 77 +19 / 77 +1/77=1.
ì0,
при
x £ 0
|
F (x) =
при 0 < x £ 1
|
при
1 < x £ 2
ïî1,
при
2 < x
Построим график функции распределения F (x)
ì0,
при
x £ 0
|
Ответ: F (x) =
при 0 < x £ 1
|
при
1 < x £ 2
ïî1,
при
2 < x
| xi | 0 | 1 | 2 |
| pi | 57/77 | 19/77 | 1/77 |
Задача 7. Даны независимые случайные величины X и Y заданы своими рядами распределений:
Составить закон распределения их суммы - случайной величины Z=X+Y и проверить выполнение свойства математического ожидания: М(X+Y)=M(X) + M(Y)
Решение
Найдем возможные значения zij = xi + y j
z 1 = 2 -1 = 1
z 2 = 2 + 0 = 2
z 3 = 2 + 20 = 22
z 4 = 4 -1 = 3
z 5 = 4 + 0 = 4
z 6 = 4 + 20 = 24
Находим вероятности этих значений:
p 1= P (Z =1)= P (X p 2 = P (Z =2) = P (X
=2) × P (Y =-1) =0,7 ×0,4 =0,28
=2) × P (Y =0) =0,7 ×0,1 =0,07
p 3= P (Z =22) = P (X =2) × P (Y =20) =0,7 ×0,5=0,35
p 4 = P (Z =3)= P (X p 5 = P (Z =4) = P (X
=4) × P (Y =-1) =0,3×0,4 =0,12
=4) × P (Y =0) =0,3×0,1 =0,03
p 6= P (Z =24) = P (X =4) × P (Y =20) =0,3×0,5=0,15
Упорядочив значения Z в порядке возрастания, получим закон распределения:
| zi | 1 | 2 | 3 | 4 | 22 | 24 |
| pi | 0,28 | 0,07 | 0,12 | 0,03 | 0,35 | 0,15 |
Проверим выполнение свойства математического ожидания
n
M (X) = å xi × pi
i =1
t
M (Y) = å y j × pj
j =1
= 2 × 0, 7 + 4 × 0, 3 = 2, 6
= -1× 0, 4 + 0 × 0,1 + 20 × 0, 5 = 9, 6
r
M (Z) = M (X + Y) = å zk × pk
k =1
= 1× 0, 28 + 2 × 0, 07 + 3 × 0,12 + 4 × 0, 03 + 22 × 0, 35 +
+24 × 0,15 = 12, 2
12, 2 = 2, 6 + 9, 6 Û M (X + Y) = M (X) + M (Y) (верно)
Ответ:
| zi | 1 | 2 | 3 | 4 | 22 | 24 |
| pi | 0,28 | 0,07 | 0,12 | 0,03 | 0,35 | 0,15 |
Задача 8. Задана функция распределения непрерывной случайной величины Х:
ì 0,
ï
x < 0
|
ï
x, 0 £ x £ a = 19 19
îï 1,
x > a = 19
Определить вероятность того, что в результате испытаний случайная величина Х примет значение, большее 0,3+α=19,3, но меньшее 0,7+α=19,7. Найти плотность вероятности распределения случайной величины Х и ее дисперсию.
ì 0,
ï
x < 0
|
ï19
îï 1,
x > 19
Найти:
P (19,3 < X < 19, 7),
f (x),
D (X)
Решение
Для нахождения вероятности попадания случайной величины X в заданный интервал, воспользуемся формулой:
b
P (a < X < b) = ò f (x) dx = F (b) - F (a)
a
P (19, 3 < X < 19, 7) = F (19, 7) - F (19, 3) = 1-1 = 0
Плотность вероятности есть производная от функции распределения, поэтому:
ì 0,
ï
x < 0
ì0, x Î(-¥;0)È(19;+¥)
|
ï19
ïî 0,
x > 19
îï 19
, x Î[0;19]
Для нахождения дисперсии случайной величины X сначала найдем ее матожидание. По определению математическое ожидание случайной величины Х
+¥
равно
M (X) =ò x × f (x) dx. Поэтому для рассматриваемой функции
-¥
M (X) = ò x ×
dx = = = 9,5
Для нахождения дисперсии случайной величины Х воспользуемся формулой
+¥
-¥
В нашем случае
19 3 19 3
1
D (X) = ò x 2 ×
dx - 9,52 = x
- 90, 25 = 19 - 90, 25 = 361
57 12
ì0, x Î(-¥;0) È (19; +¥)
Ответ: P (19,3 < X < 19, 7) = 0,
f (x) = ï 1
, D (X) = 361
í, x Î[0;19] 12
îï 19
Задача 9. Производится телефонный опрос потребителей некоторой продукции. Каждый потребитель независимо от других может дать положительный отзыв о
продукции с вероятностью a / 40 =19 / 40 = 0, 475. Составить закон распределения
случайной величины Х - числа положительных отзывов среди 3-х опрошенных потребителей. Найти математическое ожидание и дисперсию числа положительных отзывов среди 3-х опрошенных.
p = 0, 475
X - случайная величина числа положительных отзывов среди
3 - х опрошенных потребителей
Найти:
закон распределения случайной величины X,
M (X),
D (X)
Решение
Случайная величина X распределена по биномиальному закону распределения. В данной задаче она может принимать значения 0, 1, 2, 3. Соответствующие вероятности, будут определяться по формуле:
p = P (X
= m) = Cmpmqn - m, где q = 1 - p,
m = 0, 1, 2,3. Тогда
m n
P (X
P (X
P (X
P (X
= 0) = C 0× 0, 4750 × 0,5253 = 1×1× 0,5253 = 0,145
= 1) = C 1× 0, 4751× 0,5252 = 3× 0, 4751× 0,5252 = 0,393
= 2) = C 2 × 0, 4752 × 0,5251 = 3 × 0, 4752 × 0,525 = 0,355
= 3) = C 3× 0, 4753× 0,5250 = 1× 0, 4753×1 = 0,107
Составляем ряд распределения (закон распределения) случайной величины X:
| xi | 0 | 1 | 2 | 3 |
| pi | 0,145 | 0,393 | 0,355 | 0,107 |
Математическое ожидание и дисперсия, случайной величины X, распределенной по биномиальному закону распределения, находятся по формулам:
M (X) = np,
D (X) = npq,
Отсюда
M (X) = 3× 0, 475 = 1, 425,
Ответ:
D (X) = 3× 0, 475 × 0,525 = 0,748
| xi | 0 | 1 | 2 | 3 |
| pi | 0,145 | 0,393 | 0,355 | 0,107 |
M (X) = 1, 425, D (X) = 0,748
Задача 10. В большой партии телевизоров α=19 процентов бракованных. При продаже телевизоры проверяются по одному до тех пор, пока не будет найден качественный телевизор. При этом бракованные телевизоры отправляются обратно на завод. Какова вероятность того, что на завод будет отправлено: а) более 3 телевизоров; б) от 4 до 6 телевизоров. Найти м.о. и с.к.о. числа проверенных телевизоров.
q = 0,19 - вероятность, что телевизор окажется бракованным X - случайная величина числа некачественных телевизоров, отправленных обратно на завод
Y - случайная величина числа провереннных телевизоров
Найти:
а) P (X
> 3),
б) P (4 £ X
£ 6),
M (Y),
D (Y)
Решение
Случайная величина X имеет геометрическое распределения. В данной задаче она может принимать значения 0, 1, 2, 3,…,m,…. Соответствующие вероятности, будут определяться по формуле:
pm = P (X
= m) = qmp, где q = 1- p,
m = 0, 1, 2,3,..., m,.... Тогда
а) P (X
> 3) = 1- P (X £ 3) = 1- P (X
= 0) - P (X
= 1) - P (X
= 2) - P (X = 3) =
times; 0,81- 0,191× 0,81- 0,192 × 0,81- 0,193 × 0,81» 0, 00130
б) P (4 £ X £ 6) = P (X
= 4) + P (X
= 5) + P (X
= 6) =
= 0,194 × 0,81+ 0,195 × 0,81+ 0,196 × 0,81» 0, 00129
Случайная величина Y имеет так же геометрическое распределение, но в отличие от случайной величины X, принимает значения начиная с 1 (т.е. 1, 2, 3,…,n,…), а значит математическое ожидание и дисперсию можно найти по формулам:
M (Y) = 1,
D (Y) =
q, отсюда
p p 2
M (Y) =
D (Y) =
0,81
0,19
0,812
» 1, 235
» 0, 290
Ответ: а) P (X
> 3) = 0, 00130, б) P (4 £ X £ 6) = 0, 00129,
M (Y) = 1, 235,
D (Y) = 0, 290
Задача 11. К киоску в среднем подходят α=19 покупателей в час. Считая поток покупателей простейшим, найти вероятность того, что за 2 часа к киоску подойдет: а) менее 2 покупателей; б) хотя бы 1 покупатель. Найти м.о. и с.к.о. числа покупателей за 1 час.
l = 19 - интенсивность потока (среднее количество покупателей в час)
X - случайная величина числа покупателей за 2 часа Y - случайная величина числа покупателей за 1 час
Найти:
а) P (X < 2),
б) P (X ³ 1),
M (Y),
s (Y)
Решение
Поскольку поток покупателей является простейшим, то случайная величина X
имеет распределение Пуассона.
Параметр распределения Пуассона: a = l ×D t =19× 2 = 38. Теперь, используя формулу
Пуассона, найдем искомые вероятности:
P (X < 2) = P (X = 0) + P (X = 1); P (X ³1) =1- P (X = 0).
По формуле Пуассона:
P (X = m) = a
× e - a.
|
0 1
Тогда
P (X = 0) = a
× e - a = e -38;
P (X = 1) = a
× e - a = 38 e -38
Теперь
0! 1!
P (X < 2) = e -38 + 38 e -38= 39» 1, 22×10-15;
e 38
P (X ³ 1) = 1- e -38» 1
Для случайной величины Y параметр распределения будет равен
a * = l ×D t * =19×1 =19. Используем формулы для числовых характеристик распределения Пуассона:
M (Y) = a * = 19; D (Y) = a * =19; s (Y) =
Ответ: а) P (X < 2) = 39,
e 38
б) P (X ³ 1) = 1-
1,
e 38
M (Y) = 19, s (Y) =
Задача 12. Вероятность появления бракованного изделия при массовом производстве равна 0,002. Определить вероятность того, что в партии из 800+10α=990 изделий окажется не более двух бракованных.
p = 0, 002
n = 990
X - случайная величина числа бракованных изделий
Найти: P (X £ 2)
Решение
Число изделии в партии велико, а вероятность бракованного изделия очень мала, рассматриваемые события (i -ое изделие оказалось бракованным) независимы, поэтому имеет место формула Пуассона:
m
P (X = m) = a
m!
× e - a, где a = np,
отсюда
a = 990 × 0, 002 = 1, 98
0 1 2
P (X £ 2) = P (X = 0) + P (X = 1) + P (X = 2) = a
× e - a + a
× e - a + a
× e - a =
1 é a 2ù 1 é
1, 982 ù
0! 1! 2!
= × 1+ a + = × 1+1, 98 +» 0, 682
ea ê 2 ú e 1,98 ê 2 ú
ë û ë û
Ответ: P (X £ 2) = 0, 682
Задача 13. При измерении большого земельного участка его длина округляется до ближайшего целого числа метров. Какова вероятность того, что возникающая при этом ошибка а) не превысит α+10=29 см; б) будет лежать в пределах от α+5=24 см до 60 см. Найти м.о. и с.к.о. ошибки округления.
X
X - случайная величина ошибки округления
Найти:
a) P (0£ X £29),
б) P (24£ X £60),
M (X),
s (X)
Решение
Случайная величина X имеет равномерное распределение с функцией распределения:
ì 0,
ï -
x < a
ì 0,
ï
x < 0
|
b - a
a £ x £ b Û F (x) = ï x, 0 £ x £ 50
|
ï ï
îï 1,
x > b
îï 1,
x > 100
Следовательно,
P (0£ X £29) = F (29) - F (0) =29 -0 =0,58
P (24£ X £60) = F (60) - F (24) =1-24 =0,52
Математическое ожидание и среднее квадратическое отклонение найдем из формул:
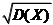
a + b
M (X) =
Тогда,
, s (X) = =
2
M (X) = 0 +50 = 25
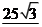(50 - 0)2
s (X) = =
12 3
Ответ:
а) P (0£ X £29) =0,58,
б) P (24£ X £60) =0,52,
M (X) = 25,
s (X) = 25 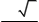3
3
Задача 14. К киоску покупатели подходят в среднем через каждые α=19 минут. Киоск начинает работу в 9 часов утра. Считая поток покупателей простейшим, найти вероятность того, что между 3 и 4 покупателем (от начала рабочего дня) пройдет: а) не менее α+2=21 минут; б) от α+1=20 до α+3=22 минут. Найти м.о. и дисперсию времени от 10 часов утра до первого после этого времени покупателя.
l = 1
Найти:
a) P (T ³21),
б) P (20£ T £22),
M (T),
s (T)
Решение
Выберем за единицу времени 1 минуту, тогда интенсивность пуассоновского потока покупателей λ = 1/19 чел/мин.
а) Вероятность P(T ³ t) того, что промежуток времени Т между двумя любыми соседними событиями в простейшем потоке будет не меньше t определяется по формуле:
P (T ³ t) = e - lt, t ³0
В нашем случае t = 21 мин:
- 1 ×21
P (T ³21) = e 19
» 0,331, t ³ 0
б) Вероятность того, что промежуток времени между двумя соседними событиями в потоке не меньше a и не больше b определим по формуле:
P (a £ Т £ b) = e - la - e - lb,
- 1 ×20
т. е.
- 1 ×22
P (20£ Т £22) = e 19
- e 19
» 0, 035
Теперь найдем математическое ожидание: до 10 часов в среднем придут 4 покупателя с промежутком в 19 мин (в 9.00, 9.19, 9.38, 9.57), следующий покупатель придёт уже после 10 часов, т.е. в 10.16 часов. Следовательно, τ = 16 мин. Тогда математическое ожидание находим по формуле:
M (Т) = lt =
1 ×16 = 16,
19 19
Дисперсия: D (Т) = lt =16
Ответ: а) P (T ³21)»0,331,
б) P (20£ Т £22)»0,035,
M (Т) =16,
D (Т) =16
19 19
Задача 15. Случайная величина имеет нормальное распределение с математическим ожиданием 2 a = 38 и средним квадратическим отклонением
a = 19. Найти вероятность того, что ее значение а) будет отрицательным;
б) будет лежать в пределах от -1 до 3;
в) будет отличаться от среднего не более чем на 2.
X
M (X) = a = 38
s = 19
Найти:
а) P (X < 0)
б) P (-1 £ X в) P (X - a
£ 3)
£ 2)
Решение
а) Вероятность попадания нормально распределенной случайной величины в заданный интервал (α;β) определяется формулой:
æ b - a ö æ a - a ö
P (a < X < b) = Ф 0ç s
÷ - Ф 0 ç s
÷, где
x z 2
è ø è ø
Ф 0 (x) =
1 -
ò e 2 dz -
функция Лапласа,
значения которой находим
по соответствующей таблице. Тогда
P (X < 0) = P (-¥ < X < 0) = Ф
æ 0 -38 ö +0,5=
0 ç 19 ÷
è ø
=- Ф 0(2) +0,5=-0, 4773 +0,5=0,0227
б) Отметим свойства непрерывных случайных величин:
P (a < X < b) = P (a £ X £ b) = P (a < X £ b) = P (a £ X < b),
следовательно
P (-1 £ X £ 3) = Ф
æ 3 -38 ö - Ф
æ -1-38 ö»
0 ç 19 ÷ 0 ç 19 ÷
è ø è ø
» Ф 0(-1,8421) - Ф 0(-2,0526) =-0,4673 +0,4799 =0,0127
в) Вероятность попадания нормально распределенной случайной величины в интервал (a-ε; a+ε), симметричный относительно центра рассеяния a, найдем по формуле:
æ e ö
P (X - a
< e) = 2 Ф ç ÷,
|
следовательно
P (X - a
£ 2) = 2 Ф
æ2 ö» 2 × 0, 0419 = 0, 0838
Ответ:
0 ç 19 ÷
а) P (X < 0) = 0, 0227,
|
в) P (X - a
£ 2) = 0, 0838
Задача 16. В результате измерения массы большого числа яблок некоторого сорта установлено, что масса одного яблока лежит в пределах от a +100 =119 до
10 a + 200 = 390 граммов. Считая, что масса яблока – случайная величина, имеющая нормальное распределение, и используя правило «трех сигм», найти математическое ожидание и с.к.о. массы яблока. Найти вероятность того, что масса случайно выбранного яблока больше a + 200 = 219 граммов.
X
P (119 £ X £ 390)» 0,9973
Найти:
M (X) = a, s,
P (X
> 219)
Решение
Запишем правило «трёх сигм»:
P (X - a < 3 s) = P (-3 s + a < X < 3 s + a)» 0,9973
По свойству непрервных случайных величин имеем
P (119 £ X £ 390) = P (119 < X < 390)» 0,9973
Найдем неизвестные параметры, решив систему уравнений:
|
|
í í
2 a = 509 ì
|
- í
a = 254,5
î3 s + a = 390
(390 a)
ï s =
271
ï s =» 45,17
î 3 î 6
Найдем неизвестную вероятность, для чего воспользуемся формулой вероятности попадания нормально распределенной случайной величины в заданный интервал:
æ b - a ö æ a - a ö
P (a < X < b) = Ф 0ç s
÷ - Ф 0 ç s
÷, откуда
P (X
è ø è ø
> 219) = P (219 < X < +¥) = 0,5 - Ф
æ ö
ç219 - 254,5 ÷»
0 ç 271 ÷
ç ÷
è 6 ø
»0,5+ Ф 0(0,7860) =0,5+0,2841 =0,7841
Ответ: M (X) = a = 254,5,
s =271,
6
P (X
> 219) = 0,7841
Задача 17. Проведена серия из 15 экспериментов со случайной величиной X. По результатам наблюдений получена выборка значений этой случайной величины. Для α =19 эта выборка имеет вид:
| ; | ; | ; | ; | ; | ; | ; | ; | ; | ; | ||||||||||
| ; | ; | ; | ; | . |
По данной выборке требуется:
1) построить дискретный вариационный ряд
2) определить численное значение моды Mo и медианы Me
3) построить ряд распределения частот
4) построить выборочную функцию распределения и ее график
5) найти несмещенную оценку генеральной средней
6) найти смещенную и несмещенную оценки генеральной дисперсии и соответствующие оценки среднего квадратичного отклонения
Решение
1) Построим дискретный вариационный ряд. Для этого проранжируем (упорядочим в порядке возрастания) значения случайной величины X
| ; | ; | ; | ; | ; | ; | ; | ; | ; | ; | ||||||||||
| ; | ; | ; | ; | . |
2) Определим численное значение моды Mo и медианы Me:
Мода – наиболее часто встречающееся значение признака.
Mo =23, т.к. это значение встречается здесь чаще всего, а именно 5 раз.
Медиана – возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части.
Ряд содержит нечетное число значений признака, поэтому медиана определятся по ее номеру:
NMe
= n +1, где n – общее число членов ряда. Отсюда
2
NMe
=15 +1 =8,
2
Me = 23, т.к. номеру 8 соответствует значение случайной величины, равное 23.
3) Построим ряд распределения частот.
Ряд распределения частот – таблица. В ее верхней строке - значение
признака xi
(варианта), в нижней строке частота варианты
mi.
| xi | ||||||
| mi |
4) По ряду распределения частот построим выборочную функцию
распределения и ее график:
F ˆ (x) = mx
n
, где mx
– число вариант меньших х,
n - объем выборки. Объем выборки: n =1+3+3+5 +2 +1=15.
Найдем искомую выборочную функцию распределения:
ì0,
при
x £ 20
|
при 20 < x £ 21
ï4 / 15,
|
ï12 / 15,
ï
ï14 / 15,
ï
при при при при
21 < x £ 22
22 < x £ 23
23 < x £ 24
24 < x £ 25
î1,
при
x > 25
5) Найдем несмещенную оценку генеральной средней.
Несмещённой оценкой генеральной средней является выборочная средняя, определяемая по формуле
n
å xi mi
x = i =1,
n
где xi
- индивидуальное значение признака (варианта).
Составим расчетную таблицу (с помощью программы MS Excel)
| № п/п | xi | mi | ximi | (xi - x) mi |
| 6,0844 | ||||
| 6,4533 | ||||
| 0,6533 | ||||
| 1,4222 | ||||
| 4,7022 | ||||
| 6,4178 | ||||
| ∑ | - | 25,7333 |
n
å ximi 337
x = i =1 =» 22, 47
n 15
6) Найдем смещенную и несмещенную оценки генеральной дисперсии и соответствующие оценки среднего квадратичного отклонения. Смещенной и несмещенной оценками генеральной дисперсии служат соответственно выборочная дисперсия и исправленная выборочная дисперсия. Воспользуемся данными расчетной таблицы.
n
å i i
(x - x)2 m
D = i =1 = 25, 7333» 1, 7156 -
смещенная
(выборочная)
дисперсия,
тогда
n 15
соответствующее среднеквадратическое отклонение s = =» 1, 3098
S 2 =
n D =
15 ×1, 7156» 1,8381 -
несмещенная (исправленная выборочная)
n -1 15 -1
дисперсия, тогда среднеквадратическое отклонение S = =» 1, 3558
Задача 18. Проведена серия из 30 экспериментов со случайной величиной X. По результатам наблюдений получена выборка значений этой случайной величины. Для α =19 эта выборка имеет вид:
| ; | ; | 20,5 | ; | ; | 21,5 | ; | ; | ; | ; | 19,5 | ; | ; | |||||||
| ; | ; | 19,5 | ; | 24,5 | ; | 23,5 | ; | ; | ; | ; | 22,5 | ; | ; | ||||||
| 20,5 | ; | ; | ; | ; | ; | ; | ; | ; | ; | 21,5 | . |
По данной выборке требуется:
1) построить интервальный вариационный ряд, определив количество групп по формуле Стерджесса;
2) определить численное значение моды Mo и медианы Me;
3) дать графическое изображение ряда в виде гистограммы частот, полигона и кумуляты;
4) построить выборочную функцию распределения;
5) найти несмещенную оценку генеральной средней;
6) найти смещенную и несмещенную оценки генеральной дисперсии (т.е. выборочную дисперсию и исправленную выборочную дисперсию) и соответствующие оценки среднего квадратичного отклонения.
Решение
1) Для построения интервального вариационного ряда, проранжируем значения случайной величины Х
| ; | ; | ; | ; | 19,5 | ; | 19,5 | ; | ; | 20,5 | ; | 20,5 | ; | ; | ||||||
| ; | 21,5 | ; | 21,5 | ; | ; | ; | ; | ; | ; | ; | ; | ||||||||
| 22,5 | ; | ; | ; | ; | 23,5 | ; | ; | ; | 24,5 | ; | ; | . |
Определим размах вариации (т.е. разность между максимальным и минимальным значениями признака):
R = x max - x min = 25 -19 = 6
Количество групп (интервалов) по формуле Стерджесса:
m»1+ 3,322lg n =1+3,322lg30» 5,91,
где n – общее число единиц совокупности.
Принимаем m=6 (округляется всегда в большую сторону). Теперь найдем величину интервала:
h = R = 6 = 1
m 6
Получаем интервальный вариационный ряд
| № интервала | Интервалы случайной величины (xi-xi+1) | Частота, mi | Накопленные частоты, Si |
| 19-20 | |||
| 20-21 | |||
| 21-22 | |||
| 22-23 | |||
| 23-24 | |||
| 24-25 | |||
| ∑ | - | - |
2) На основании интервального ряда построим вспомогательную таблицу
| № интервала | Интервалы случайной величины (xi-xi+1) | Частота, mi | Относите льная частота Pi= mi/n | Плотность частоты mi/h | Плотность относитель ной частоты Pi/h | Накопленные частоты, Si |
| 19-20 | 6/30 | 6/30 | ||||
| 20-21 | 3/30 | 3/30 | ||||
| 21-22 | 4/30 | 4/30 | ||||
| 22-23 | 8/30 | 8/30 | ||||
| 23-24 | 4/30 | 4/30 | ||||
| 24-25 | 5/30 | 5/30 | ||||
| ∑ | - | - |
Находим значения моды и медианы
Наибольшая частота, равная 8, соответствует интервалу 22-23, т.е. мода должна находиться в этом интервале и ее величину определим по формуле:
Mo = xMo
+ h ×
PMo - PMo -1, (PMo - PMo -1) +(PMo - PMo +1)
где
xMo =22 – нижняя граница модального интервала;
h = 1 – длина частичного интервала;
Дата добавления: 2016-11-24; Мы поможем в написании ваших работ!; просмотров: 6737 | Нарушение авторских прав Лучшие изречения:
<== предыдущая лекция
|
следующая лекция ==>
| Программа социологического исследования
| 2326 - 