Методом деления отрезка пополам

Пусть непрерывная функция f(x) имеет значения разных знаков на концах отрезка [ a, b ], т.е. f(a)∙f(b)<0, тогда уравнение f(x) =0 имеет корень внутри этого отрезка, который называется отрезком локализации корня.

Пусть с = (а+b)/2 – середина отрезка [ a, b ]. Если f(a)∙f(c)≤0, то корень находится на отрезке [ a, с ], который принимается за новый отрезок локализации корня. Если f(a)∙f(c)>0, то за новый отрезок локализации корня возьмем [ с, b ].

Процесс деления отрезка локализации корня продолжается до тех пор, пока его длина не станет меньше  – точности нахождения корня. На рис. 1.55 приведены результаты нахождения корня уравнения с точностью 0,0001.

 

Рис.1.55. Нахождение корня уравнения

 

В ячейку D1 (рис. 1.55) введена погрешность нахождения корня. За первоначальный отрезок локализации корня выбран отрезок [-0,2; 0,2]. В ячейки A5, B5, C4, D4, E4 и F5 введены, соответственно формулы (рис. 1.56, рис. 1.57):

=ЕСЛИ(D4<=0;A4;C4)

=ЕСЛИ(D4<=0;C4;B4)

=(A4+B4)/2

=(A4-0,2*SIN(A4+0,5))*(C4-0,2*SIN(C4+0,5))

=C4-0,2*SIN(C4+0,5)

=ЕСЛИ(B4-A4<$D$1;"Корень равен "&ТЕКСТ(C4;"0,0000");"")

Эти формулы протаскиваем вниз по столбцам до тех пор, пока не будет найден корень. Корень уравнения равен 0,1155.

 

Рис. 1.56. Нахождение корня уравнения. Режим индикации формул

 

Рис. 1.57. Нахождение корня уравнения. Режим индикации формул

 

Графический способ решения уравнения

Уравнение f(x) = 0 можно представить в виде f₁(x) = f₂(x). Заданное уравнение преобразуем к виду .

Далее строим графики y = f₁(x) и y = f₂(x). Находим точку пересечения графиков (рис. 1.58). Грубое значение корня равно 0,1162.

 

 

Рис. 1.58. Графический способ решения уравнения

ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ ПРАКТИЧЕСКОЙ РАБОТЫ

Вариант 1

1. Построить в разных системах координат при х Î [-2, 2] графики следующих функций:

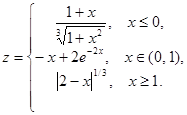
2. Построить в одной системе координат при х Î [-2, 2] графики следующих двух функций: y = 2sin(x)cos(x), z = 3cos²(2x)sin(x).

3. Построить поверхность z = x² – 2y² при х, у Î [-1, 1].

4. Найти все корни уравнения: x³ – 2,92x² + 1,4355x + 0,791136 = 0.

Вариант 2

1. Построить в разных системах координат при х Î [-2, 2] графики следующих функций:

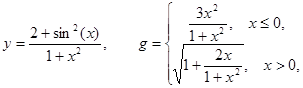
2. Построить в одной системе координат при х Î [-2, 2] графики следующих двух функций: y = 2sin(px) – 3cos(px), z = cos²(2px) – 2sin(px).

3. Построить поверхность z = 3x² – 2sin²(y)y² при х, у Î [-1, 1].

4. Найти все корни уравнения: x³ – 2,56x² – 1,3251x + 4,395006 = 0.

 

Вариант 3

1. Построить в разных системах координат при х Î [-2, 2] графики следующих функций:

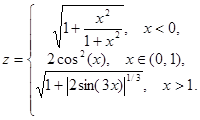
2. Построить в одной системе координат при х Î [-2, 2] графики следующих двух функций: y = 5sin(px) - cos(3px)sin(px), z = cos(2px) – 2sin³(px).

3. Построить поверхность z = 5x²cos²(y) – 2y²e^y при х, у Î [-1, 1].

4. Найти все корни уравнения: x³ + 2,84x² – 5,6064x – 14,766336 = 0.

 

Вариант 4

1. Построить в разных системах координат при х Î[-2, 2] графики следующих функций:

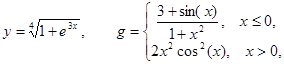
2. Построить в одной системе координат при х Î [-2, 2] графики следующих двух функций: y = 3sin(2px)cos(px) – cos²(3px), z = 2cos²(2px) – 3sin(3px).

3. Построить поверхность z = 5x² – 3cos²(y)y² при х, у Î [-1, 1].

4. Найти все корни уравнения: x³ + 1,41x² – 5,4724x –

7,380384 = 0.

 

Вариант 5

1. Построить в разных системах координат при х Î [-2, 2] графики следующих функций:

2. Построить в одной системе координат при х Î [-0, 3] графики следующих двух функций: y = 2sin(2px)cos(px), z = cos²(px)sin(3px).

3. Построить поверхность z = 2x²cos²(x) – 2y² при х, у Î [-1, 1].

4. Найти все корни уравнения: x³ + 0,85x² – 0,4317x –

0,043911 = 0.

 

 

Вариант 6

1. Построить в разных системах координат при х Î [-2, 2] графики следующих функций:

2. Построить в одной системе координат при х Î [-3, 0] графики следующих двух функций: y = 3sin(3px)cos(2px), z = cos³(4px)sin(px).

3. Построить поверхность z = 2e^0,2xx² – 2y⁴ при х, у Î [-1, 1].

4. Найти все корни уравнения: x³ - 0,12x² – 1,4775x –

0,191906 = 0.

Вариант 7

1. Построить в разных системах координат при х Î [-2, 2] графики следующих функций:

2. Построить в одной системе координат при х Î [-3, 0] графики следующих двух функций: y = 2sin(2px)cos(4px), z = cos²(3px) - cos(px)sin(px).

3. Построить поверхность z = x² – 2e^0,2yy² при х, у Î [-1, 1].

4. Найти все корни уравнения: x³ + 0,77x² – 0,2513x –

0,016995 = 0.

Вариант 8

1. Построить в разных системах координат при х Î [-2, 2] графики следующих функций:

2. Построить в одной системе координат при х Î [-0, 2] графики следующих двух функций: y = sin(3px) + 2sin(2px)cos(3px), z = cos(px) - cos(3px)sin²(px).

3. Построить поверхность z = 2x² – y² при х, у Î [-1, 1].

4. Найти все корни уравнения: x³ + 0,88x² – 0,3999x –

0,037638 = 0.

 

Вариант 9

1. Построить в разных системах координат при х Î [-2, 2] графики следующих функций:

2. Построить в одной системе координат при х Î [0, 2] графики следующих двух функций: y = cos(3px)sin(px) + 2sin(3px)cos(2px), z = cos²(px) - cos(3px).

3. Построить поверхность z = x² – 3cos²(y)y при х, у Î [-1, 1].

4. Найти все корни уравнения: x³ + 0,78x² – 0,8269x +

0,146718 = 0.

 

Вариант 10

1. Построить в разных системах координат при х Î [-2, 2] графики следующих функций:

2. Построить в одной системе координат при х Î [0, 2] графики следующих двух функций: y = 2sin(2px)cos(px) sin(3px), z = cos(2px)sin²(px) - cos(4px).

3. Построить поверхность z = 3x²sin²(x) – 5e^2yy при х, у Î [-1, 1].

4. Найти все корни уравнения: x³ + 2,28x² – 1,9347x –

3,907574 = 0.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Функции рабочего листа Excel. Список функций. Синтаксис функций. Аргументы.

2. Функции рабочего листа Excel. Функции даты и времени.

3. Функции рабочего листа Excel. Функции просмотра и ссылок.

4. Функции рабочего листа Excel. Математические и тригонометрические функции.

5. Функции рабочего листа Excel. Логические функции.

6. Опции вкладки Формулы.

7. Использование Мастера функций при вводе формул. Всплывающие подсказки.

8. Табличные вычисления. Ввод формул. Операторы.

9. Относительные, абсолютные и смешанные адреса ячеек.

10. Табличные вычисления. Режимы вычислений. Копирование формул.

11. Табличные вычисления. Значения ошибок. Использование «трассировщиков» для проверки зависимостей на рабочих листах.

12. Табличные вычисления. Имена в формулах. Использование ссылок в формулах.

13. Настройка Ленты через диалоговое окно Параметры Excel.

14. Мастер Подбор параметра. Настройка. Применение.

15. Построение и оформление диаграмм. Элементы диаграмм. Типы диаграмм.

16. Создание диаграммы при помощи мастера Диаграмм.

17. Работа с диаграммами. Опции вкладки Конструктор.

18. Работа с диаграммами. Опции вкладки Макет.

19. Работа с диаграммами. Опции вкладки Формат.

20. Редактирование диаграмм. Средства форматирования диаграмм. Обработка диаграммы.

21. Размещение диаграммы на листе. Вывод диаграммы на печать.

22. Основные этапы построения графика.

23. Основные этапы построения графика с одним условием.

24. Основные этапы построения графика с двумя условиями.

25. Основные этапы построения графиков двух функций в одной системе координат.

26. Основные этапы построения поверхности.

27. Опции вкладки Данные.

28. Нахождение корней уравнения методом последовательных приближений.

29. Нахождение корней уравнения методом деления отрезка пополам.

30. Графический способ решения уравнения.