Решить задачу аппроксимации экспериментальных данных – значит построить уравнение регрессии. Задача аппроксимации возникает в случае необходимости аналитически, то есть в виде математической зависимости, описать реальные явления, наблюдения за которыми заданы в виде таблицы, содержащей значения показателя в разные моменты времени или при разных значениях независимого аргумента. Например,
- известны показатели прибыли (их можно обозначить Y) в зависимости от размера капиталовложений (X);
- известны объемы реализации фирмы (Y) за шесть недель ее работы. В этом случае, X – это последовательность недель.
Иногда говорят, что требуется построить эмпирическую модель. Эмпирической называется модель, построенная на основе реальных наблюдений. Если модель удается найти, можно сделать прогноз о поведении исследуемого явления и процесса в будущем и, возможно, выбрать оптимальное направление ее развития.
В общем случае задача аппроксимации экспериментальных данных имеет следующую постановку:
Пусть известны данные, полученные практическим путем (в ходе n экспериментов или наблюдений), которые можно представить парами чисел (х i; уi). Зависимость между ними отражает таблица:
| X | х1 | х2 | х3 | … | хn |
| Y | y1 | y2 | y3 | … | yn |
Имеется класс разнообразных функций F. Требуется найти аналитическое (т.е. математическое) выражение зависимости между этими показателями, то есть надо подобрать из множества функций F функцию f, такую что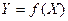 
. которая наилучшим образом сглаживала бы экспериментальную зависимость между переменными и по возможности точно отражала общую тенденцию зависимости между X и Y, исключая погрешности измерения и случайные отклонения.
Выяснить вид функции можно либо из теоретических соображений, либо анализируя расположение точек (хi; уi) на координатной плоскости.
Графически решить задачу аппроксимации означает, провести такую кривую 
, точки которой (хi; ŷi) находились бы как можно ближе к исходным точкам (хi; уi), отображающим экспериментальные данные.
Для решения задачи аппроксимации используют метод наименьших квадратов.
При этом функция считается наилучшим приближением к 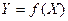, если для нее сумма квадратов отклонений «теоретических» значений 
, найденных по эмпирической формуле, от соответствующих опытных значений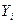 
, имеет наименьшее значение по сравнению с другими функциями, из числа которых выбирается искомое приближение.
Математическая запись метода наименьших квадратов имеет вид:
(1)
где n - количество наблюдений показателей.
Таким образом, задача аппроксимации распадается на две части.
Сначала устанавливают вид зависимости 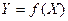и, соответственно, вид эмпирической формулы, то есть решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой. Если нет каких-либо теоретических соображений для подбора вида формулы, обычно выбирают функциональную зависимость из числа наиболее простых, сравнивая их графики с графиком заданной функции.
После этого определяются численные значения неизвестных параметров выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим.
Простейшим видом эмпирической модели с двумя параметрами, используемой для аппроксимации результатов экспериментов, является линейная регрессия, описываемая линейной функцией:
где а, b - искомые параметры.
Для модели линейной регрессии метод наименьших квадратов (1) запишется:
(2)
Для решения (2) относительно а и b приравнивают к нулю частные производные:
В итоге для нахождения a и b надо решить систему линейных алгебраических уравнений вида:
(3)
Реализовать метод наименьших квадратов в случае линейной регрессии в Excel можно различными способами.
1 способ. Построить систему линейных алгебраических уравнений, подставив в (3) все известные значения, и решить ее, например, матричным методом (см. зад. 4).
Рис. 25
В формульном виде элемент расчетной таблицы приведен на рис. 26.
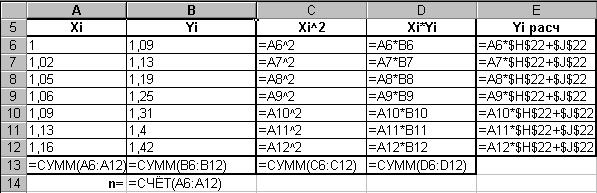
Рис.26
2 способ. Решить в Excel задачу оптимизации (2), применив для этого Поиск решения (см. зад. 5).
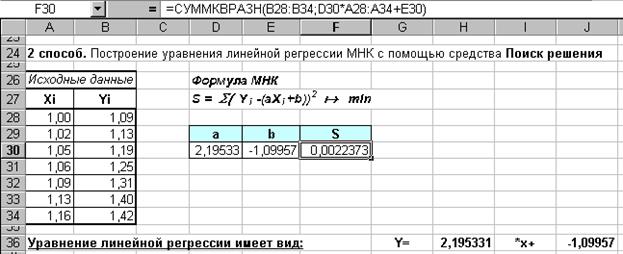
Рис.27
Замечание 1. Следует обратить внимание, что для целевой функции S удобно применить встроенную математическую функцию СУММКВРАЗН(массив1;массив2), в результате которой как раз и вычисляется сумма квадратов разностей двух массивов. В нашем случае следует в качестве массива1 указать диапазон исходных значений 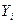, а в качестве массива2 – «теоретические» значения , рассчитанные по формуле 
, где a и b – это адреса ячеек с искомыми значениями.
Замечание 2. В диалоговом окне команды Поиск решения следует задать целевую ячейку, направление цели – на минимум и изменяемые ячейки (рис. 28). Данная задача ограничений не содержит.
Рис.28
Замечание3. В качестве эмпирических моделей с двумя параметрами могут использоваться и нелинейные модели вида:
Описанный способ решения метода наименьших квадратов применим и для нелинейных зависимостей.
3 способ. Для нахождения значений параметров a и b в случае линейной регрессии можно использовать следующие встроенные в Excel статистические функции:
НАКЛОН(известные_значения_У; известные_значения_Х)
ОТРЕЗОК(известные_значения_У; известные_значения_Х)
ЛИНЕЙН (известные_значения_У; известные_значения_Х)
Причем, функция НАКЛОН () возвращает значение параметра а, функция ОТРЕЗОК() возвращает значение параметра b. Функция ЛИНЕЙН() возвращает одновременно оба параметра линейной зависимости, так как является функцией массива. Поэтому для ввода функции ЛИНЕЙН() в таблицу надо соблюдать следующие правила:
· выделить две рядом стоящие ячейки
· ввести формулу
· по окончании нажать одновременно комбинацию клавиш Ctrl+ Shift+Enter.
В результате в левой ячейке получится значение параметра а, а в правой – значение параметра b.
Для решения задачи аппроксимации графическим способом в Excel надо построить по исходным данным график, например, точечную диаграмму со значениями, соединенными сглаживающими линиями (см.зад.1). На эту диаграмму Excel может нанести Линию тренда. Линию тренда можно добавить к любому ряду данных, использующему следующие типы диаграмм: диаграммы с областями, графики, гистограммы, линейчатые или точечные диаграммы.
При создании линии тренда в Excel на основе данных диаграммы применяется та или иная аппроксимация. Excel позволяет выбрать один из пяти аппроксимирующих линий или вычислить линию, показывающую скользящее среднее.
Кроме того, Excel предоставляет возможность выбирать значения пересечения линии тренда с осью Y, а также добавлять к диаграмме уравнение аппроксимации и величину достоверности аппроксимации (R2). Также, можно определять будущие и прошлые значения данных, исходя из линии тренда и связанного с ней уравнения аппроксимации.
Чтобы добавить линию тренда к ряду данных надо:
1. Активизировать щелчком мыши диаграмму.
2. Выполнить команду Диаграмма, Добавить линию тренда или переместить указатель на ряд данных, щелкнуть правой кнопкой мыши, а затем в контекстном меню выбрать команду Добавить линию тренда. В появившемся окне Линия тренда раскрыть вкладку Тип (рис. 29)
3. В списке Построен на ряде – выделить ряд данных, к которому нужно добавить линию тренда (Рис.29).
4. В группе Построение линии тренда (аппроксимация и сглаживание) выбрать один из шести типов аппроксимации (сглаживания). – линейная, логарифмическая, полиномиальная, степенная, экспоненциальная, скользящее среднее (Рис.29)
Рис.29
5. Чтобы установить параметры линии тренда надо раскрыть вкладку Параметры диалогового окна Линия тренда (рис. 30)
Рис.30
Показывать уравнение на диаграмме – осуществляет вывод уравнения аппроксимации на диаграмму в виде текстового поля.
Поместить на диаграмму величину достоверности аппроксимации R2 – осуществляет вывод на диаграмму достоверности аппроксимации в виде текста.
6. По окончании нажимают экранную кнопку ОК.
Пример результирующей диаграммы приведен на рисунке 31.
Рис.31
