Расчёт осветительной системы, состоящей из двух плосковыпуклых линз с параллельным ходом лучей между ними.
Исходные данные:
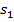 - положение источника
- положение источника
 - линейное увеличение
- линейное увеличение
 – угол охвата конденсора
– угол охвата конденсора
 - показатель преломления для основной длины волны (λ=0,555 мкм)
- показатель преломления для основной длины волны (λ=0,555 мкм)


Рисунок 1 – Схема конденсора, состоящего из двух плосковыпуклых линз
Определим световой и полный диаметры компонентов

 – припуск на закрепление при креплении
– припуск на закрепление при креплении
 – наименьшая толщина положительной линзы по краю
– наименьшая толщина положительной линзы по краю

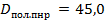 – полный диаметр по нормальному ряду
– полный диаметр по нормальному ряду
С помощью метода приближений найдём значение отрезка 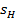 :
:
Изначально, зададися значением отрезка 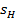 как:
как:

Считать надо до тех пор, пока значение отрезка  от двух приближений не станет равным (в 4 приближении получено значение 8,9800, а после в 5 опять такое же – значит, отрезок посчитан окончательно).
от двух приближений не станет равным (в 4 приближении получено значение 8,9800, а после в 5 опять такое же – значит, отрезок посчитан окончательно).
Расчет будем сводить в Таблицу 1
Таблица 1
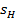
|

|

| 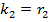 + + 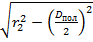
|

| 
| |
| 4,3560 | -52,0560 | -25,6220 | -13,36 | 15,4 | 10,320 | |
| 10,320 | -58,0203 | -28,5576 | -10,99 | 13,0 | 8,7120 | |
| 8,7120 | -56,4120 | -27,7660 | -11,50 | 13,5 | 9,0470 | |
| 9,0470 | -56,7470 | -27,9309 | -11,38 | 13,4 | 8,9800 | |
| 8,9800 | -56,6800 | -27,8979 | -11,40 | 13,4 | 8,9800 |
В итоге мы получили следующие значения:


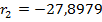
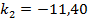

Определим конструктивные параметры линз
Из условия параллельности пучка между линзами:

Увеличение в параксиальной области:

Тогда радиус кривизны первой поверхности второй линзы:
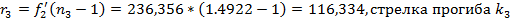
 , тогда толщина второй линзы
, тогда толщина второй линзы
 3
3  3
3  min
min 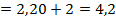
В ходе расчета нами были получены следующие конструктивные параметры:
Всегда записывайте получившуюся систему именно так:
| ne | νe | Марка стекла | Dсв | Dполн | ||
 =∞ =∞
| ||||||
| d1=13,4 | 1,4922 | 64,93 | ЛК-4 | 42,5 | 45,0 | |
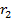 =-27,8979 =-27,8979
| ||||||
| d2=0,2 | ||||||
 = 116,334 = 116,334
| ||||||
| d3=4,2 | 1,4922 | 64,93 | ЛК-4 | 42,5 | 45,0 | |
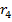 =-∞ =-∞
| ||||||
| Σd=17,8 |
Контроль линейного увеличения
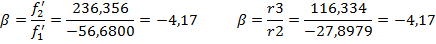
Аберрационный анализ в области аберраций 3-го порядка
Определим продольную сферическую аберрацию
Продольная сферическая аберрация определяется суммированием аберраций
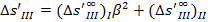 , где
, где

- продольная сферическая аберрация первой линзы в обратном ходе лучей.

- продольная сферическая аберрация второй линзы в прямом ходе лучей.




Определение поперечной сферической аберрации:




Кружок рассеяния в плоскости наименьшего кружка:

Оценка качества изображения
Для системы, состоящей из тонких компонентов:

ПНК – плоскость наименьшего кружка.

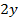 -размер предмета(6,53)
-размер предмета(6,53)

Определим величину эффективного увеличения
Что такое эффективное увеличение?
Это увеличение в плоскости наименьшего кружка. Эта плоскость смещена относительно плоскости Гаусса(ее также называют плоскостью изображения и в ней же проводится анализ) на (3/4)  , кружок рассеяния в этой плоскости в 4 раза меньше кружка рассеяния в плоскости Гаусса.
, кружок рассеяния в этой плоскости в 4 раза меньше кружка рассеяния в плоскости Гаусса.
Для его определения вводим систему БЕЗ ТОЛЩИН!
Нжимаем Esc и F9, выписываем  и
и 
Если цифры очень большие(сотни тысяч), то что-то не так. Подгоните под тысячи-сотни.


Необходимо сделать распечатку для конденсора, состоящего из двух плосковыпуклых линз. Оценивать кружок рассеяния будем у второго конденсора.
1.Ввести систему. Исходные данные для ввода:
NP – количество поверхностей (4)
NL – количество длин волн для анализа (3)
2Y – размер предмета (линейное поле) (6,53 – размер нити накала)
n*sinσ – числовая апертура (n=1, так как система в воздухе, а σ=24°)
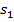 - положение предмета (предметом является нить накала) (задано, -47,7)
- положение предмета (предметом является нить накала) (задано, -47,7)
r – радиусы кривизны для 2 и 3 поверхности
d - толщины (0,2 – воздушный промежуток между линзами)
Среда – стекло ЛК4

2.Поправить показатели преломления для основной длины волны:

3.Нажать Esc и проверить линейное увеличение β:

На скрине B0 = -4,16998, нам же задано  , значит, все посчитано верно.
, значит, все посчитано верно.
4.Произвести сохранение файла и его последующую печать.
6 – 3 – прокрутить вниз – нажать два раза Esc – нажать F1 – стереть Backspace – написать новое имя – нажать Enter – нажать 1,2,3,4,5 – нажать Enter – искать файл в папке.
Место для распечатки
2.Расчёт конденсорной системы, состоящей из апланатического мениска и линзы, рассчитанной на минимум сферической аберрации.
В апланатическом мениске исправлена сферическая аберрация и кома (отсюда он и апланатический)!
Исходные данные:


Рисунок 1 – Схема конденсора, состоящего из апланатического мениска и линзы, рассчитанной на минимум сферической аберрации.
Определим световой и полный диаметры мениска:
 =
= 
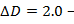 припуск на закрепление при креплении
припуск на закрепление при креплении
 – наименьшая толщина положительной линзы по краю
– наименьшая толщина положительной линзы по краю


Первая апланатическая поверхность линзы концентрична предмету, следовательно  , вторая апланатическая поверхность удовлетворяет условию апланатичности
, вторая апланатическая поверхность удовлетворяет условию апланатичности  =>
=> 
Найдем радиус кривизны второй поверхности из уравнения первого параксиального луча при выполнении условия апланатичности:

После преобразования получаем:

Рассчитаем стрелку прогиба на первой поверхности:
 1
1 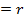 1
1 
Тогда толщина мениска
 , где
, где  2
2 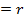 2
2 





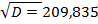
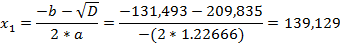

Так как первая линза имеет форму мениска, выбираем 
Рассчитаем стрелку прогиба
 2
2 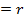 2
2 
Толщина мениска  1
1  min
min 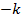 2
2 
Уточним значение второго радиуса:
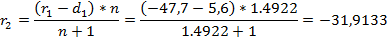
Найдём величину отрезка 

Определим увеличение линзы, рассчиатнной на минимум сферической аберрации:
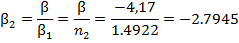
Значение отрезка  :
:

Апертурные лучи, образующие с оптической осью углы 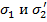 удовлетворяют условию синусов, поэтому
удовлетворяют условию синусов, поэтому

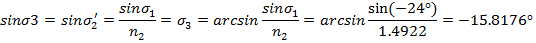

Рассчитаем вторую линзу, приняв её за бесконечно тонкую, при следующей нормировке начальных координат первого вспомогательного луча:


Примем 
Вычислим радиусы кривизны второй бесконечно тонкой линзы:


Определим световой и полный диаметр второй линзы:



Определим стрелки прогиба для второй линзы:

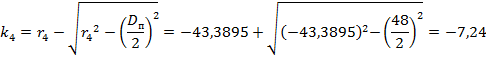
 =
=  мм
мм
Тогда

Переходим к радиусам кривизны для линзы конечной толщины

| Марка стекла | 
| 
| 
| 
| ||
| r1= -47,7 | ||||||
| d1=5,6 | ЛК4 | 1,4922 | 64,93 | 42,5 | 45,0 | |
| r2= -31,9133 | ||||||
| d2=0,2 | ||||||
| r3=86,5661 | ||||||
| d3=12,6 | ЛК4 | 1,4922 | 64,93 | 45,2 | 48,0 | |
| r4= –45,9013 |
1.Первым делом надо сделать распечатку. Вводим данные таким же способом, как и для конденсора, состоящего из плосковыпуклых линз. Получаем:
0-------------------------------------------------------------------
s1=-47.7000 n: 1.0000 1.0000 1.0000 V=0.0000
r1=-47.700000 e**2=0.000000
d1=5.6000 n: 1.4922 1.4960 1.4884 V=65.0198
r2=-31.913300 e**2=0.000000
d2=0.2000 n: 1.0000 1.0000 1.0000 V=0.0000
r3=86.566100 e**2=0.000000
d3=12.6000 n: 1.4922 1.4960 1.4884 V=65.0198
r4=-45.901300 e**2=0.000000
Delta=0.0000 n: 1.0000 1.0000 1.0000 V=0.0000
Радиус поверхности изображения: 0.000000
-------------------------------------------------------------------
ND=0 SD=0 AD=42.507776 Апертура A=0.407000
Линейное поле: 2Y=6.53 угловое: 2w= 7~49'53"
-------------------------------------------------------------------
Параксиальные характеристики
f=-46.13236 sf=-36.63710 sh=9.4952553 f'=46.132362 sf'=43.347120 sh'=-2.785242
sp=0.00000000 Dp=42.5077765 sp'=-14.741387 Dp'=53.5245357 Bp=1.25917044
s1=-47.700000 s'=235.719493 B0=-4.1700090
2w= 7~50' APW= 24~01'
-------------------------------------------------------------------
np h alpha y beta
0 * * * * -4.170009 * * * * 1.000000
1 198.909434 -4.170009 0.000000 0.670151
2 222.261485 -2.794541 -3.752848 0.942120
3 222.820393 -1.023738 -3.941272 0.616345
4 235.719493 1.000000 -11.707221 0.794174
5 -0.000000 * * * * -198.909434
-------------------------------------------------------------------
np C P W PI B Pw Bw
1 0.00000 0.00000 0.00000 -1.37547 0.00000 -0.55090 0.00000
2 -0.02115 -0.00005 -0.00001 2.29724 0.00000 0.33517 0.00000
3 -0.02723 60.76881-11.31945 0.84903 0.00000 -0.51609 0.00000
4 -0.03112 63.46764 10.34457 1.69389 0.00000 0.11078 0.00000
SIcr=-18.10708 SIIcr= 0.551116 SI= 28501.08 SII=-1176.449
SIII= 847.3884 SIV= 0.014417 SV=-105.6316 SVI=-1.308945
Зона: m= 1.000 Y= 1.000 I=-198.9094
ds'cr=-18.10708 dY'cr= 0.037723 ds'3=-162.7036 dY'3=-17.38522 K3= 1.379099
Z'm=-7.291549 Z's=-3.321352 dZ=-3.970198 dY'д= 0.016938 dSp'3= 0.001934
Осевой пучок ____Л0____ ____Л1____ ____Л2____
== M = 100tg б'== dS'=== dY'=== dS'=== dY'=== dS'=== dY'= dS'12 = Eta %=
21.254 18.29 -112.47-20.573-115.92-21.771-108.85-19.383-7.0789 45.756
18.406 13.89 -90.755-12.606-94.995-13.569-86.289-11.647-8.7057 37.252
15.026 9.95 -65.833-6.5521-71.115-7.2949-60.236-5.8118-10.879 27.244
10.627 6.16 -36.306-2.2353-43.015-2.7375-29.150-1.7344-13.865 15.140
0.000 0.00 -0.0000 0.0000-8.7341 0.0000 9.3972 0.0000-18.131
Аберрации главного луча: астигматизм,дисторсия и сф.аберрация в зрачках
Предм. 100tg W'= Y' == dY'== dY'12 = Z'm == Z's =Z'm-Z's= Sp === Sp' =
3.265 5.43 13.598-0.0169 0.0378-7.0733-3.2690-3.8043 0.000-14.739
2.308 3.84 9.6199-0.0060 0.0267-3.5887-1.6470-1.9417 0.000-14.740
Аберрации широких наклонных пучков
Зона предмета: 1.000 Меридиональное сечение
========= M d100tgб' dY(Л0) dY(Л1) dY(Л2) =Кома==================
1.000 21.254 18.207 -20.502-21.740-19.272 0.9664
0.866 18.406 13.838 -12.562-13.546-11.583 0.7779
0.707 15.026 9.942 -6.5674-7.3159-5.8219 0.5609
0.500 10.627 6.189 -2.3266-2.8217-1.8331 0.3049
0.000 0.000 -0.000 0.0000 0.0189-0.0189
-0.500-10.627 -6.452 2.9364 3.4498 2.4241
-0.707-15.026-10.439 7.6893 8.4335 6.9472
-0.866-18.406-14.547 14.118 15.071 13.169
-1.000-21.254-19.111 22.434 23.608 21.267
Сагиттальное сечение
= M 100tg E'== dY'=== dX'====================================
21.254 18.46124 0.3770-20.992
15.026 10.06154 0.2122-6.8194
Зона предмета: 0.707 Меридиональное сечение
========= M d100tgб' dY(Л0) dY(Л1) dY(Л2) =Кома==================
1.000 21.254 18.147 -20.316-21.540-19.100 0.7033
0.866 18.406 13.785 -12.408-13.385-11.436 0.5644
0.707 15.026 9.892 -6.4343-7.1803-5.6911 0.4058
0.500 10.627 6.144 -2.2134-2.7101-1.7182 0.2200
0.000 0.000 0.000 0.0000 0.0133-0.0134
-0.500-10.627 -6.334 2.6535 3.1632 2.1449
-0.707-15.026-10.251 7.2458 7.9890 6.5049
-0.866-18.406-14.298 13.537 14.492 12.586
-1.000-21.254-18.803 21.723 22.902 20.550
Сагиттальное сечение
= M 100tg E'
МЕСТО ДЛЯ РАСПЕЧАТКИ (DELTA=0)
2.Нам необходимо найти размер кружка рассеяния в плоскости наилучшей установки (там кружок будет минимальных размеров).
О чем вообще речь?
Точка изображается точкой только в идеальных оптических системах. В реальных системах имеют места кружки рассеяния. С помощью 2 графических способов нам нужно определить её положение, а также размер кружка в этой плоскости.
Способ 1:
1.Берем распечатку в руки
2.Нас интересует эта часть:
Осевой пучок ____Л0____ ____Л1____ ____Л2____
== M = 100tg б'== dS'=== dY'=== dS'=== dY'=== dS'=== dY'= dS'12 = Eta %=
21.254 18.29 -112.47-20.573- 115.92-21.771-108.85-19.383-7.0789 45.756
18.406 13.89 -90.755-12.606-94.995-13.569-86.289-11.647-8.7057 37.252
15.026 9.95 -65.833 -6.5521 -71.115-7.2949-60.236-5.8118-10.879 27.244
10.627 6.16 -36.306 -2.2353-43.015-2.7375-29.150-1.7344-13.865 15.140
0.000 0.00 -0.0000 0.0000-8.7341 0.0000 9.3972 0.0000-18.131
3. Берем миллиметровку формата А4.
Первым делом проводим оси (горизонталь и вертикаль)
Отмечаем по вертикали значение dS' для М=21,254 в масштабе (в данном случае 2:1, то есть отрезки увеличиваем в 2 раза)
По горизонтали в обе стороны откладываем увеличенный в два раза отрезок dY' в обе стороны.
Соединяем точки dY' с точкой dS'.
Тоже самое проделываем с о значениями для М=15.026
Пересечение линий dY' определяет положение плоскости наименьшего кружка, а так же его величину.
Подписываем отрезки (истинные значения, с распечатки, а не те, которые в масштабе!).

Положение плоскости наименьшего кружка мы получили 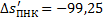
Теперь нам надо переходить в рейс и получить распечатку.
1.Открываем RAYS. Вводим систему.

2.Проверяем увеличение (лучше всегда посмотреть, получается ли то, что должно, будьте внимательны!)

3.Теперь обратите внимание на параметр Delta:

Нам нужно ввести сюда полученное значение 

4.Теперь нажимаем Esc, 6, 3

Нам нужно сделать так, чтобы эти два значения сошлись до 3 знака после запятой (желательно, конечно, полностью, но и так пойдет).
Начинаем подбор значения. Подбор выполняется, так как графически его точно достаточно сложно определить, а на ПК можно подобрать точнее.
Попробуем 98:

Уже лучше. Попробуем -96:
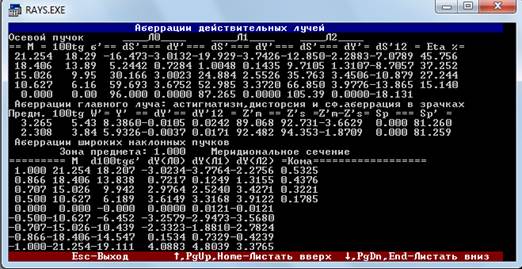
Попробуем -96,05:
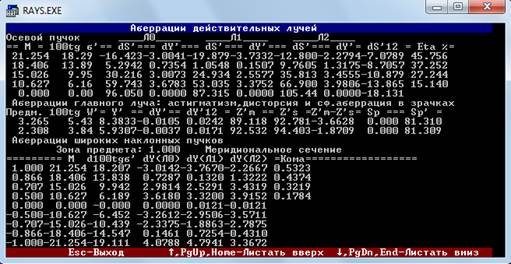
Уже лучше. Подбираем значения дальше. В итоге получаем -96,039:

Все сходится до третьего знака, все сделано хорошо.






