Конспект лекций
Лекция №4
Лектор потока: Зелёв Александр Павлович (доцент кафедры начертательной геометрии и черчения).
Прямая, перпендикулярная плоскости
| Рассматривается построение комплексного чертежа прямой, перпендикулярной к плоскости общего положения. Из курса средней школы: прямая перпендикулярна плоскости, если она перпендикулярна одновременно к двум пересекающимся прямым данной плоскости. При работе с комплексным чертежом удобно использовать в качестве этих пересекающихся прямых горизонталь и фронталь, так как к этим линиям уровня удобно строить проекции перпендикуляров. | ||
| Дана плоскость Г(АВС) и точка М вне плоскости Г. Пусть требуется через точку М построить прямую n, перпендикулярную плоскости Г. | 
| |
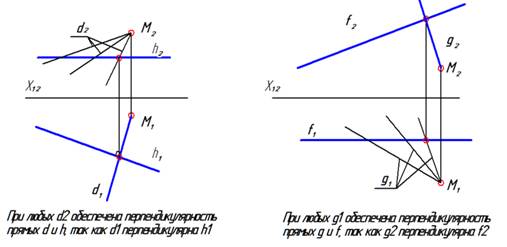
| Из курса средней школы: При построении прямой, перпендикулярной плоскости, нужно построить две пересекающиеся прямые в данной плоскости. Затем следует строить новую прямую так, чтобы она была перпендикулярна одновременно к этим двум пересекающимся прямым данной плоскости. Причем, вовсе не обязательно, чтобы новая прямая пересекалась с этими двумя прямыми, принадлежащими плоскости. Новая прямая, в общем случае, скрещивается с ними. При работе с комплексным чертежом: Для прямой, перпендикулярной к горизонтали, нужно, чтобы ее горизонтальная проекция была перпендикулярна к горизонтальной проекции горизонтали. При этом, фронтальная проекция строящейся прямой может быть любой. Для прямой, перпендикулярной к фронтали, нужно, чтобы ее фронтальная проекция была перпендикулярна к фронтальной проекции фронтали. При этом, горизонтальная проекция строящейся прямой может быть любой. | ||
| ||
| Следуя этой логике, строим n1 перпендикулярно h1 и n2 перпендикулярно f2. Так как n1 перпендикулярна h1, прямая n перпендикулярна плоскости Г(АВС) при любой фронтальной проекции n2. Так как n2 перпендикулярна f2, прямая n перпендикулярна плоскости Г(АВС) при любой горизонтальной проекции n1. Следовательно, прямая n перпендикулярна плоскости Г, так как она перпендикулярна двум пересекающимся прямым h и f плоскости Г(АВС) | 
| |
Пересечение прямой с плоскостью
| Постановка задачи. На комплексном чертеже дана плоскость и прямая, не принадлежащая данной плоскости. Требуется на комплексном чертеже определить точку пересечения прямой и плоскости. При построении чертежа требуется учесть и видимость прямой относительно плоскости. | |
| На иллюстрации изображена плоскость треугольника АВС и прямая n. Требуется найти точку М пересечении прямой n с плоскостью Σ(АВС). Алгоритм приведен на слайде: 1) прямую n заключаем в проецирующую плоскость Θ 2) строим линию пересечения плоскостей Σ и Θ. На этой прямой находятся все точки, принадлежащие двум плоскостям; в том числе – и искомая точка М. 3) Находим точку М пересечения прямой 1-2 и данной прямой n 4) Определяем видимость прямой n относительно плоскости Σ В алгоритме применяется проецирующая плоскость: ее след-проекция обладает собирательным свойством, то есть все объекты проецирующей плоскости проецируются в ее след-проекцию на плоскость, перпендикулярно которой она расположена. | 
|
| Решение задачи. Примечания: Данная прямая и проецирующая плоскость проецируются на П1 в одну прямую. Для построения фронтальной проекции линии 1-2 используем ее принадлежность к плоскости Г(АВС). Для определения видимости на П1 используем конкурирующие точки 1 и 5. Для определения видимости на П2 используем конкурирующие точки 3 и 4. | 
|






