Якщо перейти від ідеальної рідини до потоку реальної рідини треба мати на увазі такі особливості. Під час руху в'язкої рідини частина енергії витрачається на подолання сил опору, отже вздовж потоку питома енергія зменшується. Також треба урахувати нерівномірність розподілу швидкостей у перерізі потоку (рис. 2.2)
Рисунок 2.2 – Розподіл швидкостей у перерізі а – для ідеальної рідини, б – для реальної рідини
Рівняння Бернуллі для потоку реальної рідини має вигляд
. (2.7)
В цій формулі
– втрати напору на подолання гідравлічних опорів між перерізами 1 і 2;
Δp – втрати тиску на подолання гідравлічних опорів;
α – коефіцієнт Коріоліса, якій ураховує нерівномірність розподілу швидкостей у перерізі.
Гідравлічні опори
В практичних розрахунках постає потреба знайти величину втрат тиску ∆p при використанні рівняння Бернуллі (2.7). Під час руху рідини в потоках, обмежених твердими стінками (трубах, каналах) виникають деформації потоку, які призводять до дисипації енергії.
Дії на потік, які призводять до втрат енергії, називаються гідравлічними опорами.
Гідравлічні опори поділяють на два види – втрати тиску на довжині потоку і втрати тиску в місцевих опорах.
Гідравлічні опори на довжині спричиняє гальмівна дія стінок потоку, яка пов'язана з прилипанням до них рідких частинок, тобто які обумовлюються внутрішніми силами, пов'язаними з в'язкістю рідини.
Втрати тиску в місцевих опорах виникають внаслідок різких змін форми межових поверхонь, ці втрати обумовлюються дією зовнішніх сил – сил ваги, інерційних сил, пов'язаних з масою рідини.
Для визначення повних гідравлічних втрат застосовують принцип додавання втрат тиску на окремих ділянках і в місцевих опорах
, (2.8)
де Δpl – втрати тиску по довжині потоку, які пропорційні довжині каналу;
Δpмо – втрати тиску в місцевих опорах, які виникають при зміні величини та положення вектора швидкості руху рідини, тобто коли виникають прискорення, і пов'язані з ними сили інерції.
Втрати тиску Δp виникають в потоці рідини, яка рухається в каналах. Тому вони визначаються як частина швидкісного напору
або 
, (2.9)
де А – коефіцієнт пропорціональності, який показує яку частку швидкісного напору складають втрати.
Втрати тиску Δp в значній мірі залежать від режиму руху рідини в каналах. Питання про режими руху рідини докладно дослідив англійський фізик Рейнольдс О. Встановлено, що мають місце два режими руху рідини – ламінарний і турбулентний (рис. 2.3).
Рисунок 2.3 – Схема стікання рідини в різних режимах руху: ламінарне, перехідна ділянка стікання, турбулентне.
Ламінарне стікання має шаруватий характер, це рух рідини без пульсації швидкості і відбувається без перемішування частинок. Закон зміни швидкості в поперечному перерізі труби являє собою квадратичну параболу. (рис. 2.4)
Рисунок 2.4 – Схема ламінарного руху рідини
Середня швидкість в перерізі дорівнює половині максимальної 
, а коефіцієнт Коріоліса α = 2.
Турбулентне стікання – це рух рідини з пульсацією швидкості, частинки рухаються хаотично і перемішуються. Закон зміни швидкості в поперечному перерізі труби близький до логарифмічного (рис. 2.5).
Рисунок 2.5 – Схема турбулентного руху рідини
В цьому разі середня швидкість в перерізі дорівнює (0.8 – 0.9)Umax, а коефіцієнт Коріоліса α = 1.0…1.1.
Одним із найважливіших параметрів потоку є безрозмірний комплекс, який називається числом Рейнольдса:
, (2.10)
де U – швидкість потоку;
dr – гідравлічний діаметр каналу;
ν – кінематична в'язкість рідини.
Гідравлічний діаметр каналу визначається як
, (2.11)
де F – площа перерізу каналу;
П – периметр каналу.
Гідравлічний діаметр являє собою узагальнену характеристику перерізу.
Наприклад, для круглої труби
,
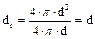тобто гідравлічний діаметр дорівнює геометричному.
Досліди Рейнольдса засвідчили, що перехід від ламінарного руху до турбулентного залежить від значення Re. Зі збільшенням числа Рейнольдса течія втрачає стійкість, і ламінарний рух перетворюється на турбулентний. У потоці виникає перемішування, в ньому утворюються вихори.
Число Рейнольдса, за якого ламінарний рух перетворюється на турбулентний й навпаки, називають критичним Reкр. Питанням нестійкості ламінарного стікання й умов переходу його в турбулентне присвячено багато досліджень. Найчастіше під час розрахунку трубопроводів приймають значення Reкр= 2100 – 2300.
Критичне число Рейнольдса не є стале, а залежить від умов входження рідини в трубу, шорсткості її стінок тощо. Значення критичного числа Рейнольдса характеризує явище гістерезису під час переходу ламінарного стікання в турбулентне й навпаки.
Якщо розраховане число Рейнольдса для конкретних умов стікання менше ніж критичне – рух ламінарний, якщо більше ніж критичне – рух турбулентний.
Втрати тиску на довжині потоку визначаються за формулою Дарсі
, (2.12)
де l – довжина каналу;
dr – гідравлічний діаметр каналу;
U – швидкість руху рідини в каналі;
ρ – густина рідини;
λ – коефіцієнт гідравлічного тертя (коефіцієнт Дарсі).
Коефіцієнт Дарсі λ залежить від режиму руху рідини, форми перерізу каналу, шорсткості поверхні каналу та інших умов. Якщо режим стікання ламінарний, коефіцієнт Дарсі може бути розрахований аналітичними методами.
Для круглого перерізу 
; для квадратного перерізу 
;
для щілинного каналу 
.
Шорсткість внутрішньої поверхні труб порушує геометричну подібність, тому величина коефіцієнта Дарсі λ залежить від форми і розташування нерівностей. Величину відношення середньої висоти нерівностей Δ до діаметра d називають відносною шорсткістю, а обернену до неї – відносною гладкістю.
Дослідні дані з визначення коефіцієнта гідравлічного тертя обробляються у вигляді залежностей (експерименти Нікурадзе): 
Теорію турбулентного стікання розроблено не досить добре, оскільки потік має складний механізм. Напівемпірічні теорії турбулентності, що були розроблені вченими Прандтлем, Карманом, Буссінеском, Альтшулем, Нікурадзе, дозволили дістати низку результатів, добре узгоджених з досвідом.
Для визначення коефіцієнта гідравлічного тертя λ запропоновано декілька емпіричних формул.
Наприклад, формула Блазіуса має вигляд
. (2.13)
Межі областей застосування різних формул для визначення λ наводяться у довідниках.
Яким чином змінюються втрати тиску при переході ламінарного стікання в турбулентне?
Розглянемо стікання рідини в круглому каналі для якого число Рейнольдса становить Re = 2200, тобто на межі критичного. Якщо стікання ламінарне, коефіцієнт Дарсі дорівнює
.
Якщо стікання турбулентне, будемо мати
.
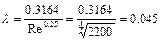Тобто, коефіцієнт Дарсі у випадку турбулентного стікання в 1.5 рази збільшився в порівнянні з ламінарним, втрати тиску згідно з (2.12) також будуть більшими.
Місцеві гідравлічні опори виникають завжди, коли швидкість змінюється за величиною – раптова чи плавна зміни перерізу, за напрямком – рух рідини в колінах, кутниках, відводах трубопроводів, за величиною й напрямком – рух рідини через апаратуру (крани, клапани, розподільники).
Втрати тиску в місцевих опорах визначають за формулою Вейсбаха
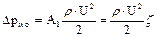, (2.13)
де ζ – безрозмірний коефіцієнт місцевого опору (або коефіцієнт місцевих втрат),
U – середня швидкість за місцевим опором.
Коефіцієнти місцевого опору для різноманітних типів опорів наводяться в довідниках [3]
Наприклад, місцевий опір в вигляді діафрагми (рис. 2.6) являє собою плоску перегородку з круглим отвором діаметром d у центрі.
Рисунок 2.6 – Місцевий опір в вигляді діафрагми
Коефіцієнт місцевого опору залежить від співвідношення діаметрів 
. При 
; ζ = 1,при 
; ζ = 70.
Другий приклад. Місцевий опір в вигляді раптового повороту труби (рис. 2.7)
Рисунок. 2.7 – Місцевий опір в вигляді раптового повороту труби
Коефіцієнт місцевого опору залежить від кута α коліна.
При α = 30º; ζ = 0.155,
при α = 90º; ζ = 1.19.
Зміна напрямку вектора швидкості приводить до виникнення сили інерції.
