Продифференцируем по времени соотношение:
,
тогда
. (7.5)
Здесь 
– касательная составляющая ускорения,
– нормальная составляющая ускорения,
– ускорение точки В вследствие вращательного движения плоской фигуры относительно полюса D. Теорема: Ускорение точки плоской фигуры равняется геометрической сумме ускорения точки, выбранной в качестве полюса и ускорения этой точки вследствие вращательного движения плоской фигуры относительно полюса.
Соотношение (7.5) изображено на рис. 25 для различных направлений углового ускорения.
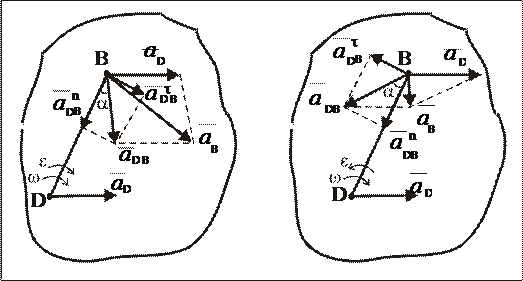
Рис. 25
На основании формул (6.4) и (6.5) получим:
, следовательно,
, 
. (7.6)
Глава 5. Сложное движение МТ
Абсолютное, относительное и переносное
Движения МТ
Определение: движение МТ, рассматриваемое одновременно относительно нескольких систем координат, хотя бы одна из которых неподвижна, называется сложным движением.
Иначе говоря, сложным движением МТ называется такое движение МТ, которое может рассматриваться состоящим из нескольких движений.
Движение МТ делится на абсолютное, относительное и переносное.
Введем неподвижную систему координат О1x1y1z1 и систему координат Oxyz, перемещающуюся относительно системы О1x1y1z1.
МТ, участвующая в сложном движении, перемещается относительно подвижной системы координат Oxyz и вместе с ней относительно неподвижной системы координат О1x1y1z1.
Определение: абсолютным движением МТ называется движение МТ относительно неподвижной системы координат.
Рис. 26
Абсолютное движение МТ – это ее движение относительно неподвижной системы координат О1x1y1z1 и ее уравнением движения будет 
(рис. 26).
Все параметры абсолютного движения обозначаются индексом "а".
Определение: относительным движением МТ называется движение МТ относительно подвижной системы координат.
Относительное движение МТ – это ее движение относительно подвижной системы координат Oxyz и ее уравнением движения будет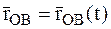 
с координатами x(t), y(t), z(t) (рис. 64).
Все параметры относительного движения обозначаются индексом "r".
Определение: переносным движением МТ называется движение относительно неподвижной системы координат той точки подвижной системы координат, в которой находится в данный момент рассматриваемая точка (иначе говоря, переносное движение МТ – это движение МТ вместе с подвижной системой координат Oxyz относительно неподвижной системы координат О1x1y1z1).
Положение подвижной системы координат определяется положением ее начала координат 
и направлениями ее осей, которые определяются единичными ортами 
.
Все параметры переносного движения обозначаются индексом "е".
