План
Угловая скорость и угловое ускорение.
Момент инерции.
Кинетическая энергия вращения.
Момент силы. Уравнение динамики вращательного движения твердого тела.
Момент импульса и закон его сохранения.
Литература
Угловая скорость и угловое ускорение
Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис. 1). Ее положение через промежуток времени Dt зададим углом Dj. Элементарные (бесконечно малые) повороты можно рассматривать как векторы (они обозначаются 
или 
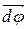). Модуль вектора 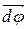равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т. е. подчиняется правилу правого винта (рис. 1). Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определенных точек приложения: они могут откладываться из любой точки оси вращения.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
Вектор 
направлен вдоль оси вращения по правилу правого винта, то есть так же, как и вектор 
(рис. 2).
Рис. 1 Рис. 2
Линейная скорость точки
то есть
Если w =const, то вращение равномерное и его можно характеризовать периодом вращения Т — временем, за которое точка совершает один полный оборот, т. е поворачивается на угол 2p. Так как промежутку времени Dt = Т соответствует Dj = 2p, то w = 2p/Т,откуда
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:
откуда
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
Тангенциальная составляющая ускорения
и
Нормальная составляющая ускорения
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор 
сонаправлен вектору 
(рис. 3), при замедленном — противонаправлен ему (рис. 4).
Рис. 3 Рис. 4
Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение аt, нормальное ускорение аn) и угловыми величинами (угол поворота j, угловая скорость w, угловое ускорение e) выражается следующими формулами:
В случае равнопеременного движения точки по окружности (e—const)
где w0 — начальная угловая скорость.
Момент инерции
При изучении вращения твердых тел будем пользоваться понятием момента инерции. Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс т материальных точек системы на квадраты их расстояний до рассматриваемой оси:
В случае непрерывного распределения масс эта сумма сводится к интегралу
где интегрирование производится по всему объему тела. Величина rв этом случае есть функция положения точки с координатами х, у, z.
Рис. 5
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси
(рис 5). Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины drсвнутренним радиусом rи внешним r+dr.Момент инерции каждого полого цилиндра dJ = r2dm (так как dr << r, то считаем, что расстояние всех точек цилиндра от оси равно г), где dm — масса всего элементарного цилиндра; его объем 2prhdr. Если r— плотность материала, то dm = 2prhrdr и dJ = 2phrr3dr. Тогда момент инерции сплошного цилиндра
но так как pR2h — объем цилиндра, то его масса m = pR2hr, а момент инерции:
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями:
(1)
В заключение приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, т — масса тела).
Таблица 1
| Тело | Положение оси | Момент инерции |
| Полый тонкостенный цилиндр радиусом R Сплошной цилиндр или диск радиусом R Прямой тонкий стержень длиной l Прямой тонкий стержень длиной l Шар радиусом R | Ось симметрии Тоже Ось перпендикулярна стержню и проходит через его середину Ось перпендикулярна стержню и проходит через его конец Ось проходит через центр шара | тR2 1/2 тR2 1/12 ml2 1/3 ml2 2/5 тR2 |
Кинетическая энергия вращения
Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 6). Мысленно разобьем это тело на маленькие объемы с элементарными массами т1, т2,..., тn, находящиеся на расстоянии гь г2,..., гn от оси.
При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами miопишут окружности различных радиусов ri и имеют различные линейные скорости vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
(2)
Рис. 6
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
или
Используя выражение (2), получаем
где Jz — момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела
(3)
Из сравнения формулы (3) с выражением для кинетической энергии тела, движущегося поступательно (E= mv2/2), следует, что момент инерции — мера инертности тела при вращательном движении. Формула (3) справедлива для тела, вращающегося вокруг неподвижной оси.
В случае плоского движения тела, например цилиндра, скатывающегося с наклон ной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
где т — масса катящегося тела; vc — скорость центра масс тела; Jc — момент инерции тела относительно оси, проходящей через его центр масс; w — угловая скорость тела.
