Каждой квадратной матрице А может быть поставлено в соответствие некоторое число, вычисляемое по определенному правилу с помощью элементов матрицы. Такое число называют определителем (или детерминантом) матрицы А и обозначают символом | А |, D или det A. При этом порядком определителя называют порядок соответствующей матрицы.
Пусть дана матрица второго порядка  .
.
Тогда определитель второго порядка матрицы А вводится по формуле:
 ,
,
где  - элементы определителя,
- элементы определителя,  ,
,  ,
,  – члены определителя.
– члены определителя.
В каждый член определителя входит по одному элементу из каждой строки и каждого столбца.
Пример 11:
 .
.
Свойства определителей:
Свойство 1: При перестановке строк матрицы на место столбцов и обратно определитель матрицы не меняется.
Пусть задана матрица 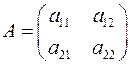 , а матрица
, а матрица 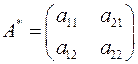 получена из
получена из  перестановкой строк на место столбцов.
перестановкой строк на место столбцов.
 называется транспонированной матрицей по отношению к
называется транспонированной матрицей по отношению к  .
.
Тогда, 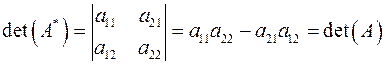 .
.
Свойство 2: При перестановке двух столбцов (или строк) абсолютное значение определителя матрицы не меняется, а знак меняется на противоположный.
Пусть задана матрица 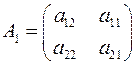 , полученная из
, полученная из  перестановкой столбцов. Тогда,
перестановкой столбцов. Тогда,
 .
.
Свойство 3: Если матрица имеет два одинаковых столбца (или строки), то определитель матрицы равен нулю.
Свойство 4: Если все элементы какого-либо столбца (строки) матрицы умножить на одно и то же число, то определитель матрицы окажется умноженным на то же число.
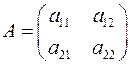 ;
;  .
.
 ;
;
 .
.
Свойство 5: Если все элементы какого-либо столбца (или строки) матрицы равны нулю, то определитель матрицы равен нулю.
Свойство 6: Если соответствующие элементы двух столбцов или двух строк матрицы пропорциональны, то  .
.
 ;
;  .
.
Свойство 7: Пусть все элементы какого-либо столбца (строки) матрицы  представляют собой сумму двух слагаемых, и пусть соответственные столбцы матрицы
представляют собой сумму двух слагаемых, и пусть соответственные столбцы матрицы  и
и  состоят из этих слагаемых.
состоят из этих слагаемых.
 ;
; 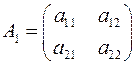 ;
;  .
.
Тогда,  .
.
Свойство 8: Определитель матрицы не меняется, если к элементам какого-либо столбца (или строки) матрицы прибавить элементы другого столбца (или строки), умноженные на одно и то же число.
Пусть 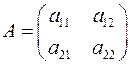 и
и  .
.
Тогда,

Замечание. Рассмотренные свойства выполняются для определителей любого порядка.
Матрице третьего порядка 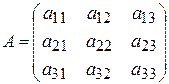 соответствует определитель
соответствует определитель
 .
.
Для запоминания знаков слагаемых и сомножителей в каждом слагаемом полезно запомнить следующее правило.
Правило Крамера (треугольников).
Определитель третьего порядка – это алгебраическая сумма шести тройных произведений. Каждое слагаемое в этой сумме содержит по одному элементу из каждой строки и каждого столбца.
Со знаком «+» берутся произведения, сомножители которых находятся на главной диагонали и в вершинах треугольников с основаниями параллельными главной диагонали

 .
.
Со знаком «-» берутся произведения, сомножители которых расположены на побочной диагонали и в вершинах треугольников с основаниями параллельными этой диагонали

 .
.
Прежде, чем сформулировать определение определителя  -го порядка, необходимо ввести понятие минора и алгебраического дополнения элементов матрицы.
-го порядка, необходимо ввести понятие минора и алгебраического дополнения элементов матрицы.
Рассмотрим определитель третьего порядка



 .
.
Выберем произвольный элемент этого определителя (для определенности  ). Минором этого элемента
). Минором этого элемента  называют определитель второго порядка, получаемый из данного вычеркиванием третьей строки и второго столбца, на пересечении которых стоит элемент
называют определитель второго порядка, получаемый из данного вычеркиванием третьей строки и второго столбца, на пересечении которых стоит элемент  :
:
 .
.
Минором  элемента
элемента  определителя
определителя 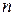 - го порядка называют определитель
- го порядка называют определитель  – го порядка, получаемый из исходного вычеркиванием
– го порядка, получаемый из исходного вычеркиванием 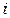 -й строки и
-й строки и  -го столбца на пересечении которых расположен элемент
-го столбца на пересечении которых расположен элемент  .
.
Алгебраическим дополнением  элемента
элемента  называют его минор, взятый с соответствующим знаком
называют его минор, взятый с соответствующим знаком  .
.
Теорема (разложение определителя по элементам строки (столбца)).
Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения
 .
.
Теорема Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Задан определитель  .
.
Для него выполняется  .
.
Вычисление определителя 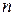 - го порядка происходит по теореме 1, причем раскладывать определитель удобнее по той строке (столбцу), в которой все элементы кроме одного равны нулю. Если такой строки нет, то ее нужно получить, применяя свойства определителей.
- го порядка происходит по теореме 1, причем раскладывать определитель удобнее по той строке (столбцу), в которой все элементы кроме одного равны нулю. Если такой строки нет, то ее нужно получить, применяя свойства определителей.
Итак, если дана матрица  -го порядка
-го порядка
 .
.
Определителем этой матрицы называется число, полученное по следующему правилу:
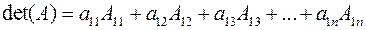 ,
,
причем  , а минор
, а минор 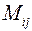 будет определителем матрицы
будет определителем матрицы  -го порядка.
-го порядка.
Пример 12: Вычислить определитель матрицы А = 

= -5 + 18 + 6 = 19.
Пример 13:. Даны матрицы А =  , В =
, В =  . Найти det (AB).
. Найти det (AB).
1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13; det (AB) = det A ×det B = -26.
2- й способ: AB =  , det (AB) = 7×18 - 8×19 = 126 –
, det (AB) = 7×18 - 8×19 = 126 –
– 152 = -26.
Пример 14:
Вычислить определитель  .
.
 = -1
= -1 
 = -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.
= -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.
 =
=  = 2(0 – 2) – 1(0 – 6) = 2.
= 2(0 – 2) – 1(0 – 6) = 2.
 =
=  = 2(-4) – 3(-6) = -8 + 18 = 10.
= 2(-4) – 3(-6) = -8 + 18 = 10.
Значение определителя: -10 + 6 – 40 = -44.






