Задача 1
Даны матрицы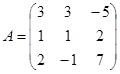 
, 
, 
.
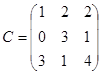1. Вычислить матрицу 4 A+ 5 C+ 7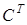 
.
2. Выполняется ли равенство AC=CA?
3. Вычислить определители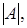 
, 
, 
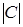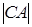и проверить равенство: = = 
.
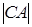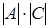4. Используя свойства определителей, вычислить определитель
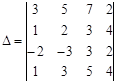
Задача 2
1. Решить систему AX=B матричным методом.
2. Решить системы уравнений по формулам Крамера:
, 
, 
.
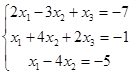3. Решить систему уравнений методом Гаусса: 
.
Задача 3. Даны векторы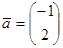 
, 
= 
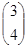. Вычислить и изобразить в системе координат следующие линейные комбинации векторов 
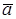и :
, 
, 
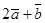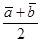
Задача 4
Найти линейную комбинацию векторов 
, = 
, 
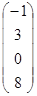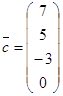с коэффициентами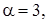 
.
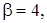
Задача 5
Будут ли векторы линейно зависимы или линейно независимы в случаях:
а) =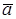 
= 
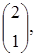
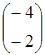; б) = 
= 
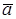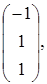
; в) = = ,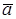 
?
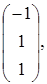
Задача 6
Даны три вектора 
= 
= 
, 
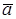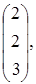
. Доказать, что система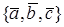 
образует базис в 
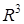. Найти разложение вектора 
по этому базису.
Задача 7. Даны два вектора = 
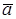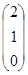и = 
. Найти 
угол 
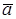между векторами и 
, а также 
.
Задача 8. При каком значении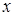 
вектор = 
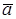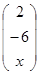ортогонален вектору = 
?
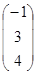При каких значениях x и y векторы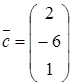 
и 
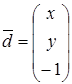параллельны?
Задача 9
Вычислить площадь и высоту треугольника с вершинами A (7;3;4), B (1;0;6) и C (4;5;7).
Задача 10
Вершины треугольной пирамиды находятся в точках 
, 
, 
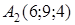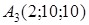и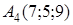 
. Вычислить: а) объем пирамиды; б) высоту, опущенную из вершины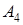 
Задача 11
Выяснить, лежат ли точки D (1;0;1), E (0;1;–3)в плоскости ABC, где A (5;–3;0), B (–4;3;3), C (–4;2;4).
Задача 12
а) Найти параметрические уравнения прямой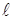 
, проходящей через точку 
параллельно вектору 
.
б) При каком значении параметра t точка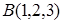 
принадлежит этой прямой?
в) Принадлежит ли точка 
этой прямой?
г) Построить данную прямую.
Задача 13
а) Составить параметрические уравнения прямой 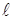, проходящей через точки 
и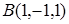 
.
б) Используя параметр, найти координаты точек C и D, делящих отрезок 
на три равные части.
Задача 14
Построить плоскости и указать особенности их расположения:
а)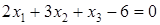 
;
б)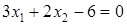 
;
в)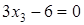 
;
г) 
;
д)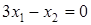 
.
Задача 15
а) Составить уравнение плоскости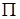 
, которая проходит через точку 
и имеет нормальный вектор 
.
б) Принадлежит ли этой плоскости точка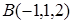 
?
Задача 17
Cоставить уравнение плоскости 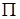, проходящей через три точки 
, 
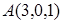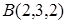и 
.
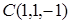Задача 18
Составить уравнение плоскости 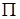, проходящей через точку 
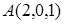и прямую 
.
Задача 19
Составить уравнение плоскости 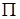, проходящей через две параллельные прямые 
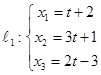и 
.
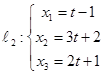Задача 20
Составить уравнение плоскости 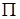, проходящей через точк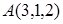и 
и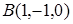 
параллельно вектору 
.
Задача 21
Составить уравнение плоскости 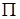, проходящей через две точки 
и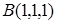 
перпендикулярно плоскости 
.
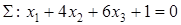Задача 22
Составить уравнение плоскости 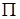, проходящей через точку 
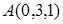параллельно плоскости 
.
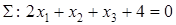Задача 23
При каком значении параметра a плоскости 
и 
будут перпендикулярны?
Задача 24
При каких значениях параметров a и b плоскости 
и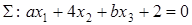 
будут параллельны?
Задача 25
Найти точку пересечения прямой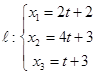 
и плоскости 
.
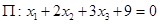Задача 26
Найти угол между прямой 
и плоскостью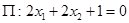 
.
Задача 27
Найти проекцию точки 
на плоскость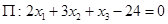 
.
Задача 28
Найти проекцию точки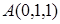 
на прямую 
.
Задача 29
Дана прямая 
. Найти угловой коэффициент этой прямой и отрезок, отсекаемый ею на оси ординат. Построить эту прямую.
Задача 30
Дана прямая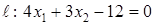 
и точка 
. Составить уравнение:
а) прямой 
,проходящей через точку A параллельно прямой ;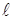
б) прямой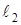 
, проходящей через точку A перпендикулярно прямой .
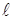Задача 31
Даны вершины 
, 
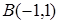и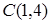 
треугольника ABC. Составить:
а) уравнение стороны BC;
б) уравнение высоты AH;
в) уравнение медианы AD.
Задача 32
Найти точку, симметричную точке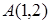 
относительно прямой 
.
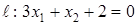Задача 33
Найти координаты какой-либо точки, принадлежащей данной кривой:
.
Задача 34. Определить тип кривой и построить ее: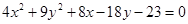 
.
Задача 35. Найти область, ограниченную линиям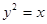и: 
и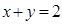 
.
Задача 36. Найти полярное уравнение и построить кривую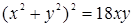 
.
Задача 37. Лежит ли точка А(-1,1,2) на поверхности, полученной вращением параболы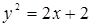 
вокруг оси Ох? Если нет, найдите, по крайней мере одну точку на этой поверхности.
Задача 38. Опишите область, которая получается в сечении фигуры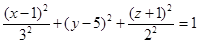 
плоскостью хОу.
Задача 39. Найдите точки пересечения прямой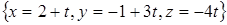 
с гиперболическим параболоидом 
.
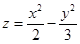