Задачи курсовой работы (семестр 1)
Группа 1 (массивы не использовать)
1.1. Определить, принадлежит ли заданная точка с координатами X и Y закрашенной области. Варианты областей:
| R1 |
| R2 |
| 1) |
| A |
| B |
| 2) |
| A |
| R |
| 3) |
| R |
| A |
| 4) |
| R |
| 5) |
| A |
| 6) |
| B |
1.2. Дано целое число К. Определить К-ю цифру в последовательности 11010010001…., в которой выписаны подряд степени числа 10.
1.3. Составить программу, которая вводит числа от 0 до 99 и печатает их в словесной форме.
1.4. Составить программу, которая печатает TRUE, если среди первых трех цифр дробной части заданного положительного вещественного числа есть цифра 5, и FALSE в противном случае.
1.5. Составить программу, которая печатает TRUE или FALSE в зависимости от того, равен ли квадрат заданного числа кубу суммы цифр этого числа.
1.6. Составить программу, которая печатает TRUE, если среди цифр заданного трехразрядного положительного целого числа есть одинаковые, и FALSE в противном случае.
1.7. Составить программу, которая печатает TRUE, если все цифры заданного положительного четырехразрядного целого числа одинаковы, и FALSE в противном случае.
1.8. Составить программу, которая определяет, является ли заданное четырехразрядное число палиндромом, т.е. таким, десятичная запись которого читается одинаково слева направо и справа налево.
1.9. Написать программу, которая для целого числа К (от 1 до 99) печатает фразу “Мне К лет”, учитывая при этом, что при некоторых значениях К слово “лет” надо заменить на слово “год” или “года”.
1.10. Составить программу, которая определяет число, получаемое выписыванием в обратном порядке цифр трехразрядного целого числа.
1.11. Известно, что из четырех чисел A1, A2, A3, A4 одно отлично от трех других, равных между собой. Присвоить номер этого числа переменной N.
1.12. Задана точка M с координатами (x, y). Определить месторасположение этой точки в декартовой системе координат (является ли эта точка началом координат, лежит на одной из координатных осей или расположена в одном из координатных углов).
1.13. Составить программу, которая меняет значения переменных A, B и C так, чтобы оказалось A >= B >= C.
1.14. Задана квадратичная функция вида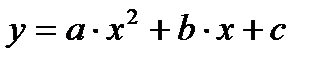 
. Вывести сообщения, как направлены ветви параболы, сколько у нее точек пересечения с осью ОХ.
1.15. Задан параллелограмм со сторонами a, b и углом α между ними. Определить тип параллелограмма (ромб, прямоугольник или квадрат), если это возможно.
1.16. Известны углы α и β у основания трапеции. Выяснить, если это возможно, тип трапеции (прямоугольная, равнобедренная, прямоугольник).
1.17. Определите, пересекаются ли парабола 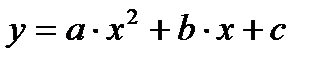и прямая 
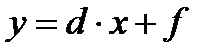. При положительном ответе найти точки пересечения.
1.18. Выяснить, пересекаются ли параболы 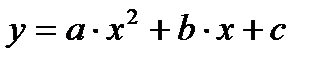и 
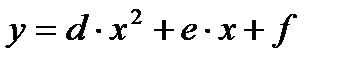. При положительном ответе найти точки пересечения.
1.19. Задана окружность с центром в точке О(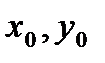
) и радиусом 
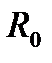и прямая 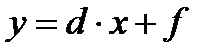. Определить, пересекаются ли прямая и окружность. При положительном ответе найти точки пересечения.
Группа 2
2.1. Для заданных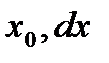 
и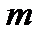 
вычислить множество значений 
, 
, 
, …, 
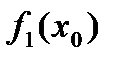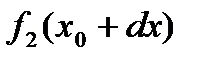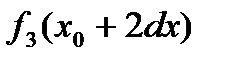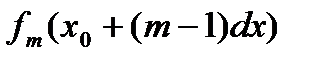функции 
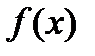в заданной области D.
2.2. Для заданных 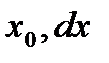и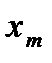 
вычислить множество значений , , , …, 
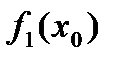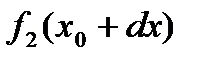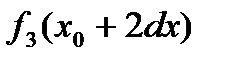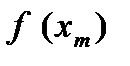функции 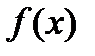в заданной области D.
При решении задач обратить внимание на проверку корректности ввода исходных данных и допустимость выполняемых вычислений.
Варианты задач (пункты 2.1 и 2.2):
| Вариант | Функция | Область определения аргумента (D) |
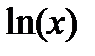
| x > 0 | |
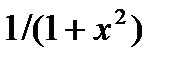
| |x| < 1 | |
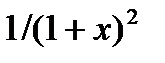
| |x| < 1 | |
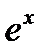
| |x| < 5 | |
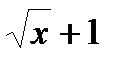
| x > 0 | |
| 1/x | 0.5 < x < 1 | |
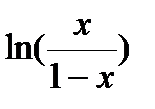
| 0 < x < 1 | |
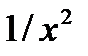
| 0.5 < x < 1 | |
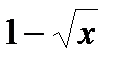
| x > 0 | |
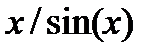
| 0 < x <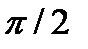 
| |
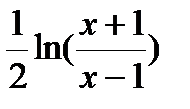
| |x| < 1 | |
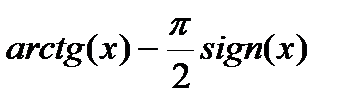
| |x| > 1 | |
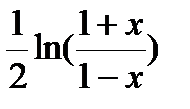
| |x| > 1 |
Группа 3
3.1. Заданы значение аргумента функции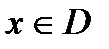 
и точность вычисления функции 
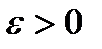(близкая к 0). Пользуясь разложением функции 
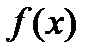в ряд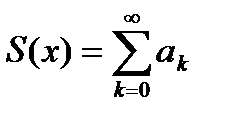 
, вычислить частичную сумму 
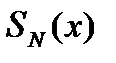, количество N членов в частичной сумме и абсолютную ошибку 
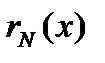приближения значения функции частичной суммой: 
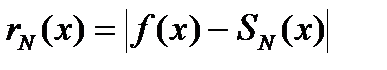. Частичная сумма вычисляется по правилу:
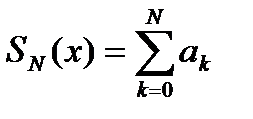, где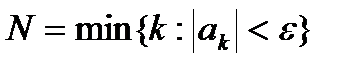 
.
Значения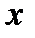 
и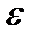 
вводятся пользователем. Функции, вид разложения и область D выбираются из следующей таблицы:
| Вариант | Функция | Вид разложения | Область D |
| 
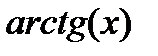
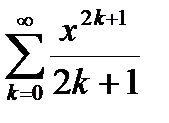
| |x| < 1 | |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
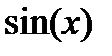
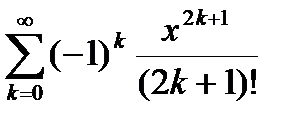
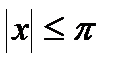
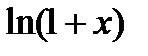
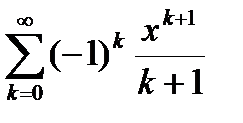
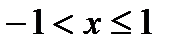
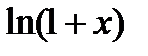
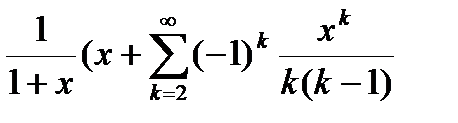
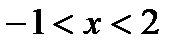
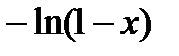
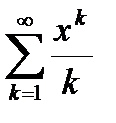
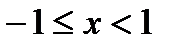
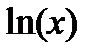
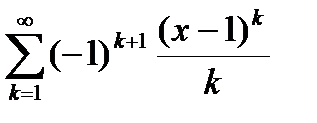
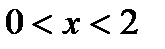
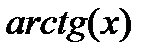
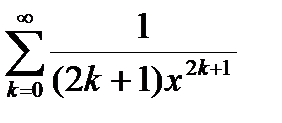
| |x| > 1 | |
|
| 
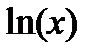
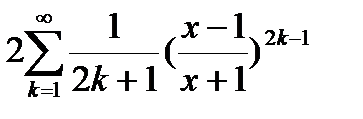
| x > 0 | |
| 
| 
| |
|
| 
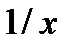
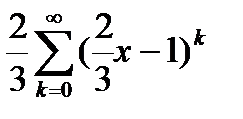
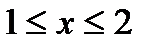
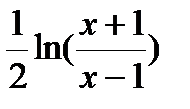
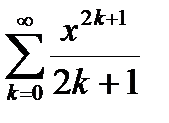
| |x| < 1 | |
|
| 
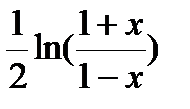
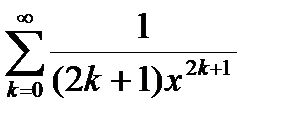
| |x| > 1 | |
|
| 
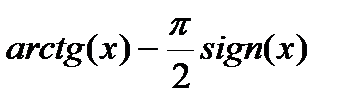
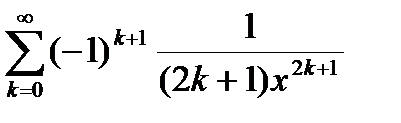
| |x| > 1 | |
| 
|
|
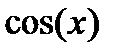
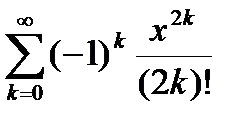
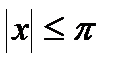
Группа 4
4.1. С клавиатуры вводится последовательность, содержащая от 1 до 50 слов, в каждом из которых от 1 до 10 строчных латинских букв и цифр. Между соседними словами произвольное число пробелов. За последним словом точка. Выполнить обработку этой последовательности в соответствии правилом, заданным в следующей таблице.
| Вариант | Правило обработки последовательности |
| Вывести на экран слова последовательности в обратном порядке без лишних пробелов | |
| Вывести на экран слова последовательности в алфавитном порядке без лишних пробелов | |
| Вывести на экран слова последовательности, не содержащие цифр | |
| Вывести на экран только те слова последовательности, в которых встречаются одинаковые буквы | |
| Вывести на экран только те слова последовательности, в которых первая буква слова встречается в этом слове еще раз | |
| После окончания ввода последовательности вывести на экран слово по его номеру в исходной последовательности и определить является ли оно корректным идентификатором языка C | |
| После окончания ввода последовательности вывести на экран сначала все слова, содержащие только буквы, затем слова, содержащие только цифры, а потом слова, содержащие и буквы и цифры | |
| Вывести на экран ту же последовательность без лишних пробелов, заменив во всех словах первую букву соответствующей прописной буквой | |
| Вывести на экран количество символов в каждом слове исходной последовательности | |
| Вывести на экран ту же последовательность без лишних пробелов, удалив из всех слов заданный набор букв и (или) цифр | |
| Вывести на экран ту же последовательность без лишних пробелов, заменив во всех словах цифры на буквы латинского алфавита, номера которых в алфавите равны заменяемой цифре | |
| Вывести на экран ту же последовательность без лишних пробелов, переместив все цифры, содержащиеся в словах, в конец соответствующих слов. | |
| Вывести все слова исходной последовательности на экран вертикально | |
| Вывести на экран все слова последовательности в две или три колонки (в зависимости от количества слов) с выравниванием слов по правой границе колонки | |
| Вывести на экран все слова последовательности в две или три колонки (в зависимости от количества слов) с выравниванием слов по левой границе колонки |
При выполнении этих заданий обратить внимание на то, что из-за произвольного числа пробелов между словами нельзя определить максимально возможную длину последовательности.
Группа 5
5.1. Дана действительная квадратная матрица порядка 2N. Получить новую матрицу, переставляя ее блоки размера N x N в соответствии с одной из схем:
5.2. Заполнить квадратную целочисленную матрицу порядка N последовательными числами от 1 до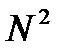 
по одной из следующих схем:
| 1 2 … |
| 1) N = 7 |
| 2) N = 8 |
5.3. Переставляя строки числовой матрицы размера M x N, упорядочить ее по убыванию элементов первого столбца.
5.4. Преобразовать квадратную числовую матрицу порядка N, переставив первую строку с последней, вторую с предпоследней и т.д.
5.5. Даны две квадратные целочисленные матрицы порядка N. Получить новую матрицу прибавлением к элементам каждого столбца первой матрицы произведения элементов соответствующих строк второй матрицы.
5.6. Переставляя строки и столбцы числовой квадратной матрицы порядка N, добиться того, чтобы наибольший элемент (один из них) оказался в верхнем левом углу.
5.7. Преобразовать целочисленную матрицу размера N x M таким образом, чтобы строка с номером K непосредственно следовала за строкой с номером Q, сохранив порядок следования остальных строк (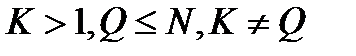
).
5.8. Определить, является ли заданная целочисленная квадратная матрица порядка N магическим квадратом.
5.9. Определить, является ли заданная целочисленная квадратная матрица порядка N ортонормированной, т.е. такой, в которой скалярное произведение каждой пары различных строк равно 0, а скалярное произведение каждой строки на себя равно 1.
5.10. Определить, является ли заданная целочисленная квадратная матрица порядка N симметричной относительно главной диагонали.
5.11. Определить, является ли заданная целочисленная квадратная матрица порядка N симметричной относительно побочной диагонали.
5.12. Напечатать индексы всех седловых точек действительной матрицы размера N x M. Элемент матрицы называется седловой точкой, если он является наименьшим в своей строке и одновременно наибольшим в своем столбце или, наоборот, наибольшим в своей строке и наименьшим в своем столбце.
Группа 6
6.1. Пользуясь рекуррентными формулами, вычислить значение многочлена степени N при заданном значении аргумента X, принадлежащего области D. Вычисление значений оформить в виде функции.
6.2. Пользуясь рекуррентными формулами, вычислить значения многочлена степеней от 0 до N при заданном значении аргумента X, принадлежащего области D. Вычисление значений оформить в виде функции.
Варианты задач (пункты 6.1 и 6.2):
| Вариант | Многочлен | Область определения аргумента (D) |
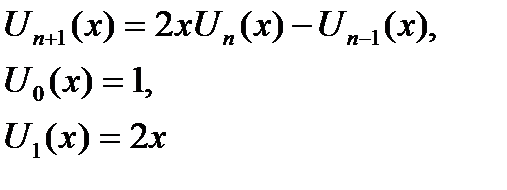
| |x| < 1 | |
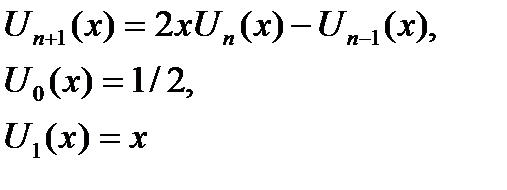
| |x| < 1 | |
| 
| |
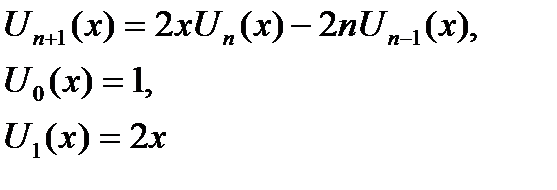
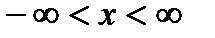
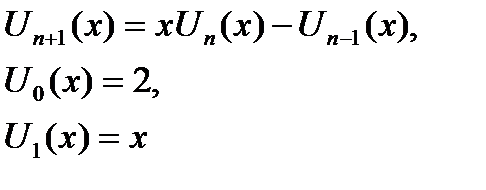
| |x| < 2 | |
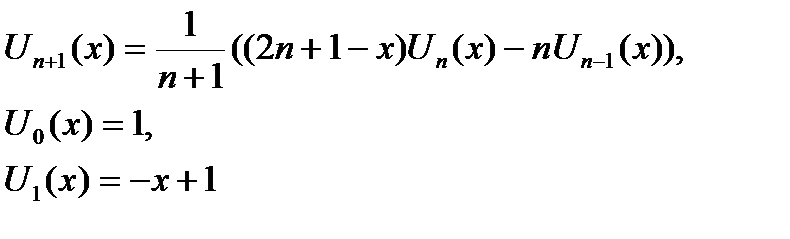
| x > 0 | |
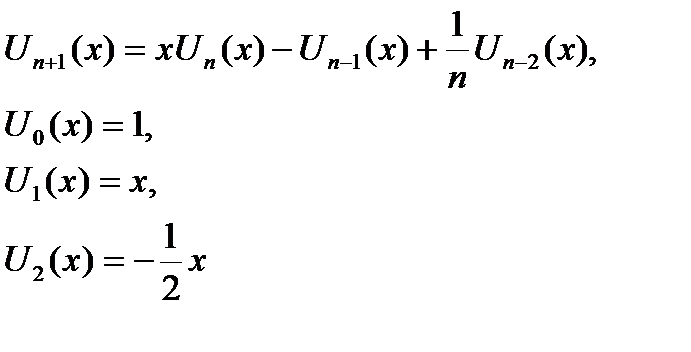
| |x| < 1 | |
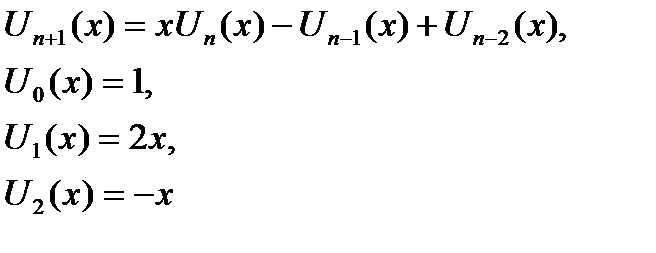
| |x| < 1 | |
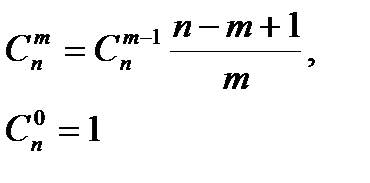
| n >= 0 и m >= n |
Группа 7
Решить задачи группы 6 с использованием рекурсивного вызова функций.
Группа 8
8.1. Используя понятие процедурного типа данных написать функцию вычисления определенного интеграла некоторой математической функции f(x) с параметрами, определяющими пределы интегрирования (a и b), точность вычисления интеграла (е) и подынтегральную функцию (f). При вычислении интеграла использовать метод прямоугольников.
8.2. Используя понятие процедурного типа данных написать функцию вычисления определенного интеграла некоторой математической функции f(x) с параметрами, определяющими пределы интегрирования (a и b), точность вычисления интеграла (е) и подынтегральную функцию (f). При вычислении интеграла использовать метод трапеций.
Тестирование разработанных в пункте 8 процедур и функций выполнить с использованием вариантов представленных в следующей таблице:
| Вариант | Функция | a | b |
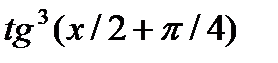
| 0.0 |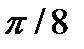 
| |
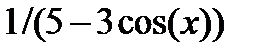
| 0.0 |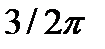 
| |
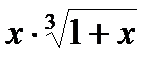
| 1.0 | 8.0 | |
| 1 / (3 + 2cos(x) | 0.0 |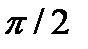 
| |
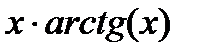
| 0.0 | 1.6 | |
 / 
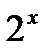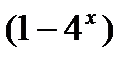
| -2.0 | -1.3 | |
|
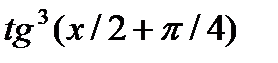
| 0.0 |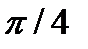 
| |
|
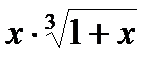
| 6.0 | 9.0 | |
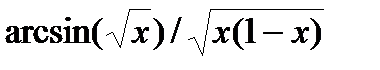
| 0.2 | 0.3 | |
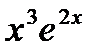
| 0.0 | 0.8 | |
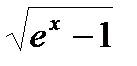
| 0.2 | 2.1 | |
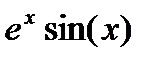
| 0.0 |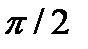
| |
| 2 / (1-4x) | -0.2 | -1.2 | |
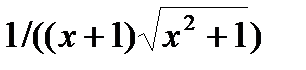
| 0.0 | 0.6 | |
|
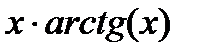
| 0.0 | 1.2 | |
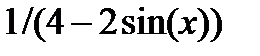
| 0.0 |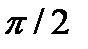
| |
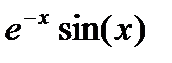
| 0.0 |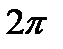 
| |
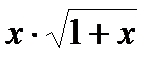
| 1.0 | 5.0 |
