Допустим, что длина горизонтальной проекции составляет 100 м. Начальная точка линии находится на горизонтали 170 м, а конечная – на горизонтали 175 м, следовательно, превышение h между точками составляет 5 м.
Тогда уклон линии АВ составит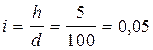 
или 5%.
Отношение превышения h к горизонтальному проложению d есть тангенс угла наклона, т.е. 
, а угол наклона линии
.
В нашем примере 
.
На практике при определении уклонов или углов наклона линий местности используется масштаб заложений (рис. 55). По горизонтальной оси отложены величины углов наклона d (или уклонов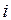 
), а по вертикальной – величины заложений d. При определении угла наклона необходимо перенести с плана на график отрезок ab таким образом, чтобы заложение d = ab было перпендикулярно оси d и находилось между этой осью и кривой графика, а затем по оси d прочитать величину угла наклона.
Рис. 55. Применение масштаба заложений для определения
угла наклона линии на местности:
а) масштаб заложений; б) топографический план участка местности
В нашем примере угол наклона линии АВ составляет 1,6°.
Определение площадей
Аналитическое определение площади. По координатам точек i замкнутой ломаной линии, ограничивающей участок местности на плане или карте, вычисляется площадь этого участка по формулам:
, 
,
т. е. площадь участка S равняется половине суммы произведений ординат каждой точки на разность абсцисс предыдущей и последующей точек или половине суммы произведений абсциссы каждой точки на разность ординат последующей и предыдущей точек.
Графическое определение площади.
Графический способ заключается в разбивке площади на простейшие фигуры, например, треугольники, а затем в суммировании площадей простейших фигур.
На рис. 56 приводится площадка, ограниченная криволинейным контуром. Контур делится прямыми отрезками 1-2, 2-3, 3-4 и т. д., которые вписываются в этот контур. Затем в произвольной точке устанавливается полюс Р, точки 1, 2, 3 соединяются с полюсом и таким образом получаются треугольники, площадь которых определяется по известной формуле.
Общая площадь, ограниченная криволинейным контуром будет равна
S = 0,5(а 1h1 + а 2h2 + а 3h3 + …+ а 10h10).
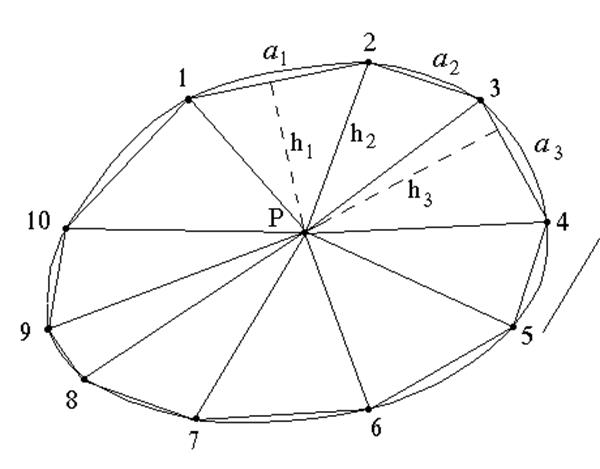
Рис. 56. Графический способ определения площадей
Определение площади с использованием палетки.
Палетка может быть квадратной, точечной и линейной (рис.9.9).
Квадратная палетка – это вычерченная на кальке квадратная сетка со стороной квадрата a. Квадратная палетка приводится на рис. 57а. Площадь одного квадрата составляет s = a 2.
Палетка накладывается на определяемую площадь и подсчитывается число целых квадратов m 1 внутри контура определяемой площади, а затем из неполных квадратов визуально составляются полные квадраты n 1.
Рис. 57. Палетки: а) –квадратная; б) – точечная; в) – линейная
Далее палетка смещается, разворачивается на 30 – 60º и определяется эта же площадь второй раз, т. е. имеем m 2 и n 2. Площадь из первого определения
S 1 = (m 1 + n 1) s,
а из второго
S 2 = (m 2 + n 2) s.
Из двух определений площади вычисляется среднее значение, если расхождение между этими определениями не превышает 1:100 измеряемой площади.
Кроме квадратной палетки применяются точечная и линейная палетки.
Точечная палетка представляет собой кальку, на которой нанесены точки вершин квадратов со стороной a. Точечная палетка показана на рис. 57б.
При измерении площади подсчитывают число точек m 1, находящихся внутри площадного контура, и число точек n 1 на этом контуре и в непосредственной близи от него.
Каждой точке из числа m 1 принадлежит площадка s = a 2,
а из числа n 1 – 0,5 s = 0,5 a 2.
Тогда измеренная площадь составит S 1 = (m 1 + 0,5 n 1) s.
Палетка смещается, разворачивается на 30 – 60º и определяется S 2 = (m 2 + 0,5 n 2) s.
Из двух определений площади вычисляется среднее значение, если расхождение между этими определениями не превысит 1:100 площади.
Линейная палетка – это параллельные линии, нанесенные на кальке (прозрачной бумаге) на одинаковом расстоянии между собой. Эта палетка приведена на рис. 57 в.
Палетку накладывают на контур измеряемой площади и подсчитывают сумму длин параллельных линий, которые находятся внутри этого контура.
Площадь вычисляется по формуле
,
где n – число параллельных линий в пределах измеряемой площади;
a – расстояние между параллельными линиями.
Палетка смещается, разворачивается на 30 – 60º и выполняется второе определение площади S 2.
Из S 1 и S 2находится среднее значение, если относительная погрешность не превышает 1:100 определяемой площади.
Определение площадей при помощи планиметра.
Планиметр – это механический прибор, при помощи которого определяется площадь, заключенная внутри контуров объектов на планах и картах. Он состоит из полюсного и обводного рычагов, счетного механизма и обводной лупы (рис. 58). По счетному механизму берется четырехзначный отсчет. В нашем примере стрелка на механизме находится между 6 и 7 тысячами, следовательно, отсчет начинается с 6 тысяч. Нуль шкалы "0 – 10" располагается между четырьмя и пятью сотнями и между тремя и четырьмя десятками, а на шкале "0 – 10" седьмой штрих совпадает со штрихом на соседней шкале. Таким образом отсчет по счетному механизму составляет 6437.
Обводная лупа устанавливается в исходной точке А контура (точка выбирается произвольно) и по счетному механизму берется отсчет О1, равный, например, 6437 (рис. 58). Обводной шпиль ведется по контуру (по ходу часовой стрелки) и останавливается в исходной точке А, берется отсчет О2, допустим, равный 6556. Разность отсчетов О2 – О1 = 0119 делений дает площадь контура в делениях планиметра.
Рис. 58. Полярный планиметр ПП-М
Если известна цена одного деления планиметра с, м 2 /дел, т. е. число квадратных метров в одном делении планиметра, тогда площадь S = c· (О2 – О1), м 2.
В нашем примере, если с = 3 м2/дел, то
S = 119 дел ·3 м 2 /дел = 357 м 2.
Цена деления планиметра вычисляется путем тройного обвода известной площади SИ по формуле
,
где SИ– известная площадь квадрата, окружности или др. правильной фигуры;
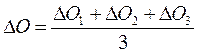– средняя разность отсчетов по планиметру.
Средняя разность D О вычисляется, если разности отсчетов
DО1 = О2 – О1, DО2 = О3 – О2 и DО3 = О4 – О3 отличаются не более чем на 2 единицы при площади до 200 делений, 3 единицы при площади 200 – 2000 делений и 4 единицы при площади свыше 2000 делений.
Пример определения цены деления приводится в табл. 3.
Таблица 3
Определение цены деления планиметра
| Отсчеты по планиметру | Разность отсчетов | Средняя разность отсчетов | Известная площадь S, м2 | Цена деления планиметра с, м2/дел. |
| О1 = 3455 | ||||
| DО1 = 111 | ||||
| О2 = 3566 | ||||
| DО2 = 113 | DО = 112 | |||
| О3 = 3679 | ||||
| DО3 = 112 | ||||
| О4 = 3791 |
Контур площади обводится дважды планиметром и вычисляется площадь в такой же таблице по формуле
,
где с – цена деления планиметра;
DО – средняя разность отсчетов по планиметру при двух обводах площади.
Таблица 4
Определение площади
| Отсчеты по планиметру | Разность отсчетов | Средняя разность отсчетов | Цена деления планиметра с, м2/дел. | Измеряемая площадь S, м2 |
| О1 = 2578 | ||||
| DО1 = 265 | ||||
| О2 = 2843 | DО = 266,5 | |||
| DО2 = 268 | ||||
| О3 = 3111 |
