Операции над машинами Тьюринга

Машина Тьюринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина).

Со­че­та­ния ал­го­рит­мов - это на­зва­ние, уста­но­вив­ше­еся за ря­дом кон­крет­ных спо­со­бов кон­стру­иро­ва­ния но­вых ал­го­рит­мов из не­ско­ль­ких за­дан­ных.

Те­оре­мы о со­че­та­ни­ях ал­го­рит­мов со­став­ля­ют важ­ный раз­дел об­щей те­ории ал­го­рит­мов. Бу­ду­чи до­ка­зан­ны­ми однаж­ды, они по­зво­ля­ют в да­ль­ней­шем убеж­да­ть­ся в осу­ще­ст­ви­мо­сти слож­ных и гро­мо­зд­ких ал­го­рит­мов без фак­ти­че­с­ко­го вы­пи­сы­ва­ния опре­де­ля­ющих их схем.

Со­че­та­ния ал­го­рит­мов для ма­ши­ны Тью­рин­га опи­сы­ва­ют­ся опе­ра­ци­ями над ма­ши­на­ми Тью­рин­га.

 

1. Опе­ра­ция ком­по­зи­ции.

Пусть M₁ и M₂ - ма­ши­ны Тью­рин­га, име­ющие оди­на­ко­вый вне­шний ал­фа­вит A«[i153] {a₀,a₁,...,a_p}. Обоз­на­чим мно­же­ст­ва их со­сто­яний со­от­ве­т­ст­вен­но Q1[i154] «[i155] {q₀,q₁,...,q_n} и Q2[i156] «[i157] {q_0',q_1',...,q_m'}.

 

 

Опре­де­ле­ние.[i158]

Ком­по­зи­ци­ей ма­шин M₁ и M₂ на­зы­ва­ют ма­ши­ну, обоз­на­ча­емую M=M₁×M₂, про­грам­ма ко­то­рой име­ет ал­фа­вит A, мно­же­ст­во со­сто­яний Q«[i159] {q₀,q₁,...,q_n,q_n+1,...,q_n+m} и по­лу­ча­ет­ся из про­грамм ма­шин M₁ и M₂ сле­ду­ющим об­ра­зом: вез­де в про­грам­ме ма­ши­ны M₁, где встре­ча­ют­ся "трой­ки" с сим­во­лом q₁ (за­клю­чи­те­ль­ное со­сто­яние ма­ши­ны M₁), он за­ме­ня­ет­ся на сим­вол q_0' (на­ча­ль­ное со­сто­яние ма­ши­ны M₂); все оста­ль­ные сим­во­лы в про­грам­мах ма­шин M₁ и M₂ оста­ют­ся не­из­мен­ны­ми (в за­вер­ше­ние оста­ёт­ся пе­ре­ну­ме­ро­вать все со­сто­яния ма­ши­ны M: {q₀,q_1'[i160],q₂,...,q_n,q_0',q_2',...,q_m'}).

 

Ком­по­зи­ция на­чи­на­ет "ра­бо­тать" как ма­ши­на M₁, но в тех слу­ча­ях, ког­да ма­ши­на M₁ до­лжна оста­но­ви­ть­ся, про­ис­хо­дит пе­ре­клю­че­ние на про­грам­му ма­ши­ны M₂, вслед­ст­вие за­ме­ны q₁[i161] на q_0'. Оче­вид­но, что опе­ра­ция ком­по­зи­ции ас­со­ци­атив­на, но не ком­му­та­тив­на.

[i161] Её работа равносильна последовательной работе машин T1 и T2 [i162].

На рисунке изображена композиция машин Тьюринга, реализующая оператор суперпозиции для n=1 и m=1.

 

Рисунок 1.

 

Опре­де­ле­ние.[i163]

Ите­ра­ци­ей ма­ши­ны Тью­рин­га M бу­дем на­зы­вать ма­ши­ну

 

2. Опе­ра­ция вет­вле­ния.

Пусть M₁, M₂ и M₃ - ма­ши­ны Тью­рин­га, име­ющие оди­на­ко­вый вне­шний ал­фа­вит A«[i164] {a₀,a₁,...,a_i,...,a_j,...,a_p} и, со­от­ве­т­ст­вен­но, мно­же­ст­ва со­сто­яний: Q1[i165] «[i166] {q₀,q₁,...,q_n}, Q2[i167] «[i168] {q_0',q_1',...,q_m'}, Q3[i169] «[i170] {q_0",q_1",...,q_l"}.

 

Опре­де­ле­ние.

[i171] Ре­зу­ль­та­том опе­ра­ции вет­вле­ния над ма­ши­на­ми Тью­рин­га M₁, M₂ и M3[i172] на­зы­ва­ет­ся ма­ши­на Тью­рин­га M, про­грам­ма ко­то­рой по­лу­ча­ет­ся из про­грамм ма­шин M₁,M₂ и M₃ сле­ду­ющим об­ра­зом: за­пи­са­на про­грам­ма ма­ши­ны M1[i173], за­тем при­пи­са­ны про­грам­мы ма­ши­ны M₂ и M₃. Ес­ли в за­клю­чи­те­ль­ном со­сто­янии q₁ ма­ши­ны M1[i174] на­блю­да­ет­ся сим­вол a_i, то управ­ле­ние пе­ре­да­ет­ся на ма­ши­ну M₂, т.е. сим­вол q₁ за­ме­ня­ет­ся сим­во­лом q_0' и на­чи­на­ет ра­бо­тать ма­ши­на M₂. Ес­ли же в за­клю­чи­те­ль­ном со­сто­янии q₁ ма­ши­ны M₁ на­блю­да­ет­ся сим­вол _a[i175] _j, то управ­ле­ние пе­ре­да­ет­ся на ма­ши­ну M₃, т.е. сим­вол q₁ за­ме­ня­ет­ся сим­во­лом q_0" и на­чи­на­ет ра­бо­тать ма­ши­на M₃. Все оста­ль­ные сим­во­лы в про­грам­мах ма­шин M₁ и M₂ оста­ют­ся не­из­мен­ны­ми. Ма­ши­на M за­вер­ша­ет ра­бо­ту в за­клю­чи­те­ль­ном со­сто­янии q₁ (в за­клю­че­ние оста­ет­ся осу­ще­ст­вить сквоз­ную пе­ре­ну­ме­ра­цию со­сто­яний ма­ши­ны M).

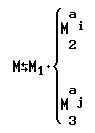
Ре­зу­ль­тат опе­ра­ции вет­вле­ния над ма­ши­на­ми Тью­рин­га M₁, M₂ и M3[i176] обоз­на­ча­ет­ся сле­ду­ющим об­ра­зом:

[i177]

Для двух­бук­вен­ных ма­шин Тью­рин­га (ма­шин Тью­рин­га с двух­бук­вен­ным ал­фа­ви­том) опе­ра­ция вет­вле­ния над про­из­во­ль­ны­ми ма­ши­на­ми Тью­рин­га M1[i178], M2 [i179] и M3[i180] обоз­на­ча­ет­ся сле­ду­ющим об­ра­зом:

т.е. ес­ли при ра­бо­те ма­ши­ны M1[i181] в со­сто­янии q₁ на­блю­да­ет­ся сим­вол a₀, то управ­ле­ние пе­ре­да­ет­ся на ма­ши­ну M2[i182], в про­тив­ном слу­чае - на ма­ши­ну M3.

 

3. Опе­ра­ция за­цик­ли­ва­ния.

Пусть M - ма­ши­на Тью­рин­га с ал­фа­ви­том A«[i183] {a₀,a₁,...,a_p} и мно­же­ст­вом со­сто­яний Q«[i184] {q₀,q₁,...,q_n}.

 

Опре­де­ле­ние.[i185]

Ре­зу­ль­та­том опе­ра­ции за­цик­ли­ва­ния бу­дем на­зы­вать ма­ши­ну Тью­рин­га, обоз­на­ча­емую (i=0,2,3,...,n; j=0,1,2,...,p; s=0,2,3,...,n)[i186]

про­грам­ма ко­то­рой по­лу­ча­ет­ся из про­грам­мы ма­ши­ны M за­ме­ной в кон­сек­вен­т[i187] е ко­ман­ды q_ia_j®q₁a_tr, rÎ{L,R,L}, [i188] t=0,1,2,...p, сим­во­ла q₁ на сим­вол q_s.

 

2[i189].4 Варианты машины Тьюринга[i190]

Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга[i191].

 

В качестве примера такой эквивалентности рассмотрим сведение любой МТ к МТ, работающая на полубесконечной ленте[i191].

Теорема: [i191] Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте.

Доказательство:

Рассмотрим доказательство Ю. Г. Карпова[i192]. Доказательство этой теоремы конструктивное, то есть мы дадим алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Во-первых произвольно занумеруем ячейки рабочей ленты МТ, то есть определим новое расположение информации на ленте:

Рисунок 1.

Затем перенумеруем ячейки, причём будем считать, что символ «*» не содержится в словаре МТ:

Рисунок 1.

2.5 Вычислимость по Тьюрингу и разрешимость[i193]

Выше было доказано, что классы функций, вычислимых с помощью рекурсивных функций, машин Тьюринга или нормальных алгоритмов Маркова, совпадают. Это позволяет рассматривать понятие «вычислительный алгоритм» инвариантным к способу описания. Различия наблюдаются лишь в использовании алгоритмических объектов. Если для рекурсивных функций объектами являются числа и числовые функции, а процесс вычисления задан операторами суперпозиции, рекурсии, минимизации и итерации, то для машин Тьюринга такими объектами являются символы алфавитов внешней и внутренней памяти, а процесс вычисления задан протоколом, использующим функции выхода, перехода и перемещения головки. Для нормального алгоритма Маркова такими объектами являются слова или последовательности символов, а процесс вычисления задан правилами подстановки или продукциями, изменяющими состав и структуру исходной последовательности символов до искомого результата.

Арифметической (числовой) функцией [i194] называют функцию, областью значений которой является подмножество множества N, а областью определения - элемент множества N.

Для алгоритмических проблем типичной является ситуация, когда требуется найти алгоритм для вычисления числовой функции f(x₁, x₂, …, x_n), зависящей от целочисленных значений аргументов x₁, x₂, …, x_n.

Функцию f:N_n→N назовем вычислимой[i195], если существует алгоритм, позволяющий для любого набора значений ее аргументов вычислить значение функции (или указать, что функция на данном наборе не определена). Так как в определении вычислимой функции используется интуитивное понятие алгоритма, то часто вместо термина «вычислимая функция» используется термин «интуитивно вычислимая функция». Таким образом, массовая проблема имеет решение, если арифметическая функция, соответствующая этой проблеме, является интуитивно вычислимой.

Функция f(x₁, x₂, …, x_n) называется эффективно вычислимой[i196], если для заданных значений k₁, k₂, …, k_n аргументов можно найти значение функции f(k₁, k₂, …,k_n) с помощью некоторой имеющейся механической процедуры (алгоритма).

Вместо уточнения понятия алгоритма можно рассматривать уточнение понятия «вычислимая функция». Обычно при этом действуют по следующей схеме:

1. Вводят точно определенный класс функций.

2. Убеждаются, что все функции из этого класса являются вычислимыми.

3. Принимают гипотезу (тезис) о том, что класс вычислимых функций совпадает с введенным классом функций.

Функция называется вычислимой[i197], если существует вычисляющий её алгоритм. «Вычислимость» является одним из основных понятий теории алгоритмов, инвариантном к вычисляемой функции и алгоритму. Различие между вычислимой функцией и алгоритмом – это различие между описанием функции и способом вычисления её значений при заданных значениях независимых аргументов.

Тезис Тьюринга[i198]. Всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.

Из тезиса Тьюринга следует, что, если возникают алгоритмические проблемы, то их следует решать на базе построения машин Тьюринга, то есть достаточно формализованного понятия алгоритма. При этом в алгоритмических проблемах часто речь идет не о построении алгоритма, а о вычислимости некоторых специальным образом построенных функций.

Следует отметить, что в этих случаях достаточно использовать алфавит {0,|}, где 0 – пустой символ. Например, натуральные числа, включая 0, в этом алфавите кодируются следующим образом: 0 - |; 1 - ||; 2 -

N - ||…| (n + 1 раз). Частичная числовая n – местная функция f(x1, x2, …, xn[i199]) называется вычислимой по Тьюрингу[i200], если существует машина М, вычисляющая ее в следующем смысле: 1. Если набор значений аргументов <x1, x2, …, xn[i201] > принадлежит области определения функции f, то машина М, начиная работу в конфигурации 0 |x1+1 0 |x2+1 [i202] … 0 |xn[i203] q1[i204] |, где |x = ||… | (x раз) ,[i205] и воспринимается самый правый символ, останавливается, заканчивая работу в конфигурации 0|yq0[i206] |, где y = f(x1, x2, …, xn). 2. Если набор значений аргументов <x1, x2, …, xn> не принадлежит области определения функции f, то машина М, начиная работу в исходной конфигурации, работает бесконечно, то есть не приходит в заключительное состояние. Машина Тьюринга есть точное формальное определение алгоритма. С помощью этого понятия можно доказывать разрешимость или неразрешимость алгоритмических проблем. Если для решения задачи, принадлежащей единому классу задач, найден алгоритм вычисления, то о задаче говорят как об алгоритмически разрешимой проблеме[i207]. Иначе говоря, обязательным условием вычислимости или результативности вычисления является её алгоритмическая разрешимость. В этом смысле понятие «разрешимость» является также основным понятием в теории алгоритмов. Анализ трех типов моделей показывает, что основные свойства дискретности, детерминизма, массовости и результативности остаются неизменными для различных способов описания: • Свойство дискретности: [i208] алгоритм состоит из отдельных элементарных действий, выполняемых по шагам; множество элементарных шагов, из которых состоит алгоритмический процесс, конечно и счетно. • Свойство детерминированности: [i209] после каждого шага дается точное указание, как и в какой последовательности выполнять следующие шаги алгоритмического процесса. • Свойство массовости: [i210] использование алгоритма допустимо для множества алгоритмических объектов данного типа и данного класса задач. • Свойство результативности: [i211] остановка алгоритмического процесса обязательна после конечного числа шагов с указанием искомого результата. Однако[i212], тезис невозможно доказать, так как он связан точным понятием вычислимости по Тьюрингу с неточным понятием интуитивно вычислимой функции.  

ПРОБЛЕМА САМОПРИМЕНИМОСТИ

Согласно определению машины Тьюринга это тройка T = <A, Q, П>, в которой A -алфавит, Q – внутренние состояния машины, Q -программа, которая и отличает одну машину от другой. В общем случае (для всех машин) программа может выглядеть, например, так:

П: q_{i a} [i213] a_{j a} [i214] ® q_{r a} [i215] a_{s a} [i216] S_{t a} [i217], a = 1, 2, …, k, где S₁ - R, S₂ - L, S₃ - C. (_*)

При этом можно считать, что существуют некоторые общие алфавиты A₀ и Q₀, в которых записываются символы a и q для всех машин Тьюринга. Тогда символы q_{i a}, a_{j a}, q_{r a}, a_{s a}, S_{t a} [i218] являются символами алфавитов A₀ и Q₀.

Такой подход позволяет все машины Тьюринга пронумеровать, то есть каждой машине присвоить некоторый номер (код), присущий только этой машине, по которому можно было бы отличать ее от других машин. Здесь рассмотрим один из способов нумерации.[i219]

Геделева нумерация машин Тьюринга. Пусть p₁, p₂, p₃, … - последовательность простых чисел, расположенная в порядке возрастания, например, 2, 3, 5, 7, 11, 13, …

Номером машины Тьюринга с программой (_*) называется число

n (T) = .

Пример

Машина, реализующая функцию S (x) = x + 1, имеет программу в алфавите {0,  [i220] }. Номер этой программы с учетом того, что a₀ = 0, a₁ = | будет число: .

n (T)= 2¹ 3¹ 5¹ 7¹ 11¹ 13¹ 17⁰ 19⁰ 23¹ 29³.

Очевидно, что не все натуральные числа являются номерами машин Тьюринга. С другой стороны, если n – номер некоторой машины, в общих алфавитах, то ее программу можно однозначно восстановить по этому номеру.

Машина T, применимая к слову n (T) (то есть к коду своего собственного номера), называется самоприменимой.

Можно построить как самоприменимые машины, так и несамоприменимые машины. Например, машина из выданного примера – самоприменима. Машина T, у которой в правых частях программы (в теле таблицы) отсутствует символ останова, неприменима ни к какому слову, а, следовательно, и к слову n (T).

Проблема самоприменимости состоит в следующем: указать алгоритм, который по любой машине Тьюринга устанавливал бы, самоприменима она или нет.

Согласно Т[i221] езису Тьюринга, такой алгоритм следует искать в виде машины Тьюринга. Эта машина должна быть применима к кодам номеров всех машин Тьюринга, и в зависимости от результата переработки кодов проверяемых машин, имела бы различные заключительные конфигурации.

Пусть, например, данная машина T применяется к коду n (T ^*). Если машина T ^* самоприменима, то заключительная конфигурация машины T имеет вид a' q₀ [i222] | B' [i223], а в случае, если машина T ^* несамоприменима, то заключительная конфигурация машины T имеет вид a" q₀ [i224] 0 B [i225] ". [i226] Здесь a', B', a", B" [i227] – слова.

Теорема Проблема самоприменимости алгоритмически неразрешима, то есть не существует машины Тьюринга, решающей эту проблему в указанном выше смысле.

Из[i228] теоремы следует, что не существует общего алгоритма решающего проблему самоприменимости. В конкретных же частных случаях такие алгоритмы могут существовать.

Воспользуемся результатами этой теоремы для доказательства неразрешимости проблемы применимости к начальному слову.

Проблема применимости к начальному слову состоит в следующем: создать алгоритм, который по машине T и слову X устанавливал бы, применима машина T к слову X или нет (иначе проблема останова).

В терминах машин Тьюринга, аналогично формулировке проблемы самоприменимости, эта проблема формулируется так: можно ли построить машину, которая была бы применима ко всем словам вида n (T)0 X, где T произвольная машина, X – произвольное слово, и в случае, если машина T применима к слову X, приводила бы к заключительной конфигурации a' q₀ [i229] |B' [i230], а в случае, если машина T не применима к слову Х, приводила бы к заключительной конфигурации a" q₀ [i231] 0 B" [i232]. Здесь a', B' и a", B" [i233] – произвольные слова.

Теорема Проблема применимости к начальному слову алгоритмически неразрешима, то есть не существует машины Тьюринга, решающей эту проблему в указанном выше смысле.

Как[i234] было вышесформулировано[i235] для проблемы самоприменимости первым предварительным шагом является нумерация. Поэтому ниже этот вопрос последовательно рассматривается и решается для алгоритмов и его трех основных типов алгоритмических моделей.

 

Нумерация алгоритмов

Нумерация алгоритмов играет важную роль в их исследовании и анализе. Поскольку любой алгоритм можно задать в виде конечного слова (представить в виде конечной последовательности символов некоторого алфавита), а множество всех конечных слов в конечном алфавите счётное, то множество всех алгоритмов также счётное. Это означает существование взаимно однозначного отображения между множеством натуральных чисел и множеством алгоритмов, то есть возможность присвоить каждому алгоритму номер.

Нумерация алгоритмов является одновременно и нумерацией всех алгоритмически исчисляемых функций, причем любая функция может иметь бесконечное количество номеров.

Существование нумерации позволяет работать с алгоритмами так же, как с числами. Особенно полезна нумерация в исследовании алгоритмов, работающих с другими алгоритмами.

Пусть имеется некая массовая проблема с множеством исходных объектов X и множеством искомых объектов Y. Для существования решения массовой проблемы необходимо, чтобы элементы множеств X и Y были конструктивными объектами. Следовательно, элементы этих множеств можно занумеровать натуральными числам. Пусть x∈[i236] X – некий исходный объект, обозначим через n(x) его номер. Если в массовой проблеме по исходному объекту x требуется получить искомый объект y∈[i237] Y с номером n(y), то определим арифметическую функцию f: Nn[i238] →N, такую что f(n(x))=n(y).

В качестве примера построения арифметических функций по массовым проблемам рассмотрим массовые проблемы.

1. Если дан массив [x1, x2, …, xn[i239] ] натуральных чисел, то ему в соответствие можно поставить натуральное число 2x1, 3x2,... p(n)xn [i240], где p(n) – n-е простое число. Рассмотрим для примера массив длины 5:

[x1, x2, x3, x4, x5[i241] [i242] ] 2x13x25x37x411x5.[i243]

Данная нумерация определяет арифметическую функцию f (например, f(73500) = f(22315372110) = 20315272113 = 4891425).[i244]

2. Любое рациональное число имеет некоторый натуральный номер. Нумерация множества искомых объектов проблемы тривиальна:

{«да», «нет»} a {1, 0}. [i245] Для данной массовой проблемы можно построить арифметическую функцию одного аргумента, воспользовавшись приемом из предыдущего примера[i246], а можно рассмотреть функцию трех аргументов (три номера элементов исходной тройки).

3. Нумерация текстов программ может быть осуществлена следующим образом: любую программу можно воспринимать как запись числа в 256-ричной системе счисления (если для записи программы использовались символы таблицы ASCII).

Переход от массовой проблемы к арифметической функции позволяет свести вопрос о существовании решения массовой проблемы к вопросу существования эффективного способа вычислений значений арифметической функции по ее аргументу (аргументам).

 

Нумерация наборов чисел

В теории алгоритмов получил распространение прием, позволяющий сводить изучение функций от нескольких переменных к изучению функций одной переменной. Он основан на нумерации наборов чисел так, что имеется биективное соответствие между наборами чисел и их номерами, причем функции, определяющие по набору чисел его номер и по номеру сам набор чисел являются общерекурсивными. Например, для функции, содержащей две независимых переменных (x, y), это отображение h(x, y) может быть таким:

[i246]

Рисунок 1.

Пусть пары (x, y) формируют частично упорядоченное множество N⁽²⁾. Если дано h(x, y) = n, то существует обратное отображение: x = h^-1₁(n) и y= h^-1₂ (n), [i247] т. е. h(h^-1₁ (n), h^-1₂ (n)) = n. Это позволяет вычислять номер n для любой пары (x, y) и, наоборот, по номеру n вычислять значения x и y:

Используя эти правила, можно вычислять нумерацию троек h²(x, y, z)[i248] = h(h(x, y), z) = n и, наоборот, по номеру тройки - значения x, y, z. Например, если h² (x, y, z) = n, то z= h^-1₂(n), y= h^-1₂ (h^-1₁ (n)), x= h^-1₁ (h^-1₁ (n)), h²(x, y, z) [i249] = h(h(h^-1₁ (h^-1₁ (n)), h^-1₂ (h^-1₁ (n))), h^-1₂ (n)). Тройки (x, y, z) формируют частично упорядоченное множество N⁽³⁾. Аналогично для произвольного количества чисел имеем:

h^n-1(x1, x2,…, xn[i250])=h(h…h(h(x1, x2), x3)…[i251] x_n-1), xn[i252]). Если h^n-1(x1, x2,…, xn[i253])=m, то xn[i254] = h^-1₂ (m), x_n-1 =h^-1₂ (h^-1₁ (m)),....................................., x2[i255] = h^-1₂ (h^-1₁ (...h^-1₁ (m)...)), x1[i256] = h^-1₂ (h (...h (m)...)).

Имея нумерацию множеств наборов N⁽¹⁾, N⁽²⁾,..., N ⁽ⁱ⁾,..., N(ⁿ, где N ⁽ⁱ⁾ – множество наборов (i) чисел, можно установить объединенную нумерацию произвольных наборов чисел M = N⁽¹⁾ N⁽²⁾ ... N ⁽ⁱ⁾ .. N(ⁿ⁾, где M N. Для любого n N имеем h(x1,x2,..., xn [i257])= h(hⁿ⁻¹(x1,x2,..., xn), n −1[i258]).

Если h(x,1x,2..., x)n[i259] = m, то hⁿ⁻¹(x,1x,2..., x)n[i260] = h^-1₁ (m), n= h^-1₂ (m)+1. Используя вышеприведенные формулы, можно восстановить значения x1, x2,…, xn. [i261]