Взаємозв’язку між факторною та
Результативною ознаками
Зміст завдання: За даними про величину факторної та
результативної ознак по сукупності підприємств:
1) визначити кореляційне рівняння зв’язку;
2) розрахувати параметри рівняння;
3) визначити показники тісноти зв’язку.
Порядок виконання
Кореляційні зв’язки характеризуються тим, що кожному значенню факторної ознаки може відповідати декілька значень результативної ознаки, а зв’язок між ними визначається лише в середньому.
Кореляційний метод аналізу дозволяє встановити наявність зв’язку, визначити його форму та виміряти силу (тісноту зв’язку). Залежно від кількості факторних ознак, взятих для аналізу, розрізняють парну та множинну кореляцію.
Рівняння, що відображає зміну середньої величини результативної ознаки (у) в залежності від факторної (х), називається рівнянням регресії або рівнянням кореляційного зв’язку.
Якщо зв’язок між факторною та результативною ознакою близький до прямолінійного, рівняння регресії буде мати вигляд:
,
де 
середнє теоретичне значення у при даному значенні х;
- параметри рівняння.
Параметр а1 (коефіцієнт регресії) визначає середню зміну результативної ознаки y при зміні факторної ознаки х на одиницю її натурального виміру.
Вибрати з додатку Г результативну та факторну ознаки і побудувати таблицю вихідних та розрахункових даних (табл. 16).
Таблиця 16
Вихідні та розрахункові дані
для обчислення рівняння зв’язку
| № підприємств | Ознаки | Розрахункові величини | Теоретичне значення результатив-ної ознаки | ||||
| факторна (…) | результат-тивна (…) | ||||||
| х | у | х2 | ху | у2 | а1 х | 
| |
| … | |||||||
| Всього |
Параметри ао та а1 визначаються на основі системи нормальних рівнянь за формулами:
 |
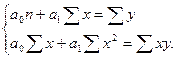
Звідки:
Після знаходження параметрів рівняння регресії приймає вигляд:
 |
Ступінь тісноти зв’язку характеризується коефіцієнтом кореляції. Для його розрахунку використовують формулу:
Оцінка коефіцієнту кореляції відбувається за такими критеріями:
r = 0 - зв’язок відсутній;
r = 0,1 – 0,3 - зв’язок слабкий;
r = 0,3 - 0,5 - зв’язок помірний;
r = 0,5 - 0,7- зв’язок суттєвий;
r = 0,7 - 0,9 зв’язок тісний;
r = понад 0,9 - зв’язок дуже тісний;
r =1 - зв’язок функціональний.
Коефіцієнт детермінації визначається як квадрат коефіцієнта кореляції:
Структурна формула середньої помилки коефіцієнта кореляції має вигляд:
Критерій надійності коефіцієнта кореляції визначається за формулою:
Якщо критерій надійності t r - перевищує величину 3, коефіцієнт кореляції не є випадковим і не спростовує наявності і суттєвості зв’язку.
Висновки:
Тема: Аналіз інтенсивності динаміки
