Выразим вероятность безотказной работы через интенсивность отказов

l(t) = f(t)/P(t) = -(1 / P(t)) * (dP(t) / dt).

Разделим переменные и произведем интегрирование

l(t)dt = - (1/P(t)) * dP(t) = - lnP(t)

l(t)dt = - lnP(t), так как lnP(0) = 0

Тогда, P(t) = exp(- l(t)dt)

f(t) = l(t) * exp(- l(t)dt).

Функция плотности вероятности f(t) и интенсивности отказов l(t) обе дифференциальные функции, относящиеся к моменту времени t и показывают долю отказавших образцов в единицу времени. Но для f(t) – эта доля по отношению к No начальному количеству образцов, а для l(t) – эта доля по отношению к N(t) количеству не отказавших образцов на момент времени t.

При l - const будем иметь

l(t) = l

P(t) = exp(-l * t).

f(t) = l * exp(-l * t).

Средняя наработка до отказа – математическое ожидание наработки до отказа. Математическое ожидание – числовая характеристика закона распределения случайной величины.

В статистической формулировке

, где t_i – наработка на отказ отдельного образца.

3.2. Классификация моделей надежности.

Математическая модель надежности – это математическое выражение, связывающее значения действующих нагрузок, физических параметров системы с показателями надежности.

Математическая модель является результатом формирования процесса изменения технического состояния системы, развития дефектов, неисправностей и потери работоспособности.

Различают модели надежности систем и их элементов.

Техническое состояние системы формируется как совокупность технических состояний отдельных элементов. Критерий отказа системы формируется из условия: ведет ли данная совокупность отказов элементов к отказу всей системы. Показатели надежности системы вычисляются через показатели надежности элементов.

Техническое состояние элемента формируется как соотношение между физическими параметрами. Критерий отказа формируется из условия превышения заданным параметром допустимого предела. Например, нагрузки над прочностью. Нагрузки могут иметь механическую, электромагнитную, тепловую, химическую и др. природу. Соответствующие прочностные свойства элемента обеспечивают стабильность его структуры.

3.3. Модели надежности систем.

3.3.1 Последовательное и параллельное соединение элементов.

Пусть система состоит из элементов, каждый из которых в свою очередь может находиться в двух возможных состояниях. Пусть состояние 0 – работоспособное состояние (работа), а состояние 1 – неработоспособное состояние (отказ) рис. 3.5.

 

Рис. 3.5 Элемент системы с двумя возможными состояниями

Последовательное соединение двух элементов рис. 3.6 (а) образует систему, которая также может находиться в двух возможных состояниях рис. 3.6 (б).

0 1

0 1

а)

 

0 1

б)

Рис. 3.6 Последовательное соединение элементов (а), образующих систему (б).

Понятие последовательного соединения элементов в смысле надежности соответствует следующему утверждению (логической функции): система работоспособна, если работоспособен и первый и второй элементы или система неработоспособна, если неработоспособен или первый, или второй или оба элемента.

Параллельное соединение двух элементов рис. 3.7 (а) образует систему, которая также может находиться в двух возможных состояниях рис. 3.7 (б).

 

0 1

а)

 

 

б)

 

Рис. 3.7. Параллельное соединение элементов (а), образующих систему (б)

Понятие параллельного соединения элементов в смысле надежности соответствует следующему утверждению: система неработоспособна, если неработоспособен и первый и второй элементы или система работоспособна, если работоспособен или первый, или второй или оба элемента.

Пусть вероятность безотказной работы (состояния 0) для каждого из элементов равна P₁ и P₂ и следует определить вероятность безотказной работы системы при последовательном и параллельном их соединении.

На основании теоремы о произведении вероятностей для независимых событий при последовательном соединении элементов вероятность безотказной работы системы равна произведению вероятностей безотказной работы отдельных элементов

P_c = P₁ * P₂.

На основании той же теоремы о произведении вероятностей при параллельном соединении элементов вероятность отказа системы равна произведению вероятностей отказов отдельных элементов

Q_c = Q₁ * Q₂.

Вероятность безотказной работы в этом случае находится как вероятность противоположного события

P_c = 1 – Q_c.

3.3.2 Модели надежности на основе марковских цепей.

Пусть система состоит из m элементов, каждый из которых может находиться в двух состояниях l = 2. При этом число возможных состояний системы равно n = l ^m.

Каждое из состояний системы отличается состоянием хотя бы одного из ее элементов. Множество возможных состояний системы составляют полную группу. В частности, все элементы могут находиться в работоспособном состоянии или все элементы могут находиться в неработоспособном состоянии.

Система подвергается последовательности циклических нагружений. Например, включений в работу. При этом элементы системы, следовательно, и вся система в целом может случайным образом переходить из одного состояния в другое. Существует термин «система блуждает по состояниям».

Пусть индекс k = 0,1,2,… соответствует номеру цикла нагружения, причем k = 0 соответствует начальному состоянию системы.

Начальным условием является распределение вероятностей нахождения системы в каждом из возможных состояний при k = 0. Ряд распределения имеет вид

p1(0), p2(0), … pi(0), …pj(0), …pn(0).

Причем Σ pi(0) = 1, i =1,n так как множество состояний системы составляет полную группу несовместных событий.

Например, если достоверно известно, что в начальный момент времени система находилась в i-ом состоянии, то pi(0) = 1, а остальные члены ряда распределения равны нулю.

Задача 1. Определить закон распределения вероятностей по возможным состояниям системы при первом цикле нагружения.

Для этого необходимо знать вероятности переходов из любого i-ого состояния в любое j-ое состояние |pij| - матрицу переходных вероятностей. Например, переходная вероятность pii – это вероятность того, что система была в состоянии i и после нагружения осталась в этом же состоянии.

Тогда, по формуле полной вероятности, вероятность того, что система, находясь в произвольном состоянии i, после первого цикла нагружения перейдет в состояние j, будет равна

pj(1) = Σ _i=1,n (pi(0)*pij); j = 1,n.

Задача 2. Определить вероятность безотказной работы системы на первом цикле нагружения.

Для этого необходимо ввести в рассмотрение вектор-столбец условных вероятностей безотказной работы для каждого из состояний, причем Рi = 1, если в i-ом состоянии система достоверно работоспособна и Pi = 0, если в i-ом состоянии система достоверно неработоспособна.

Тогда вероятность безотказной работы системы с учетом случайности возможных переходов на первом шаге нагружения будет равна

P(1) = Σ _j=1,n (pj(1)*Pj) = Σ _j=1,n ((Σ _i=1,n(pi(0)*pij))* Pj).

В матричной форме

P(1) = │pi(0)│║ pij ║ │Pj │, где

 

3.4. Модели надежности элементов систем.

3.4.1 Модель «нагрузка – прочность»

Рассматривается стационарная с непрерывными параметрами модель надежности элемента системы – вероятностная модель «нагрузка-прочность». Критерий отказа – превышение нагрузки над прочностью.

Пусть нагрузка характеризуется функцией распределения плотности вероятности приложенного электрического напряжения - f(u), где {u} – случайная непрерывная величина приложенного напряжения, а прочность характеризуется функцией распределения плотности вероятности пробивного напряжения (прочностная характеристика материала изоляции) – f(U), где {U} - случайная непрерывная величина пробивного напряжения.

Здесь обозначено: m_u – математическое ожидание приложенного напряжения, m_U – математическое ожидание электрической прочности.

Критерий работоспособности: – прочность больше или равна приложенному напряжению.

Вероятность безотказной работы элемента определяется из условия

Условная вероятность безотказной работы при условии, что приложенное напряжение равно u*

По интегральной формуле полной вероятности вероятность безотказной работы элемента для любых возможных значений нагрузки u или через функцию распределения вероятностей

 

Если f(u) и f(U) подчиняются нормальным законам распределения с параметрами m_u, m_U (математическое ожидание нагрузки и прочности) и s_U и s_u (среднее квадратическое отклонение нагрузки и прочности), то плотность вероятности разности случайных величин Z = U – u распределена также по нормальному закону

,

где - математическое ожидание,

- среднее квадратическое отклонение.

Функция распределения

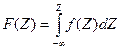
может быть выражена через функцию Лапласса («интеграл вероятности») Ф(x), для которой составлены таблицы.

.

Свойства функции Лапласа

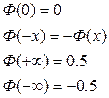
Критерий отказа Z < 0,

Критерий работоспособности Z ≥ 0.

Тогда, вероятность отказа

Вероятность безотказной работы

.

3.4.2. Модель внезапных отказов.

В период нормальной эксплуатации надежность характеризуется внезапными отказами. Эти отказы вызываются неблагоприятным стечением многих обстоятельств и поэтому имеют постоянную интенсивность, которая не зависит от старения, усталости и износа.

, где

- средняя наработка до отказа.

Из основного соотношения надежности вероятность безотказной работы

соответствует экспоненциальному закону распределения во времени и одинакова за любой одинаковый промежуток времени.

Плотность распределения

При t = T₀, P(T₀) = 0.368, следовательно Q(T₀) = 0.632, то есть 63% отказов возникнет за время Т₀.

 

3.4.3. Модель постепенных отказов.

В период износа надежность характеризуется постепенными отказами. Наиболее универсальным для практики расчета в этот период является нормальный закон распределения.

Плотность распределения

,

Статистическая оценка параметров.

Математическое ожидание , средняя наработка до отказа.

Среднее квадратическое отклонение ,

где t_i – наработка до отказа i- ого элемента.

Вероятность безотказной работы выражается через функцию Лапласа

4. Структурные схемы надежности электрических аппаратов.

Для расчета надежности прежде всего следует разработать структурную схему надежности электрического аппарата, выявить основные эксплуатационные факторы, влияющие на на­дежность, и оценить их ко­личественно. В структурную схему должны войти основ­ные узлы аппарата, подвер­женные отказам.

Для каждого элемента в структурной схеме должна быть раз­работана методика расчета надежности, основанная на математи­ческих моделях надежности этих узлов. Обычно в электрическом аппарате отказ любого элемента в структурной схеме надежности приводит к отказу электрического аппарата. Если отказы элемен­тов и узлов независимы, то вероятность безотказной работы элект­рического аппарата

,

где Pi — вероятность безотказной работы 1-го узла (всего уз­лов— g).

Если отказ одного из узлов зависит от вероятности отказа дру­гого, то для определения вероятности безотказной работы элект­рического аппарата необходимо перемножить условные вероятности безотказной работы соответствующих узлов. Если вероятность без­отказной работы отдельных узлов близка к единице, то эти узлы можно не учитывать в структурной схеме и при расчете надежно­сти электрического аппарата.