Г.
Байконур 2016г.
Цель работы:
Освоить:
· работы в среде визуального программирования Delphi;
· программного решения трансцендентного уравнения численными методами;
· разработки интерфейса приложения с использованием базовых компонентов библиотеки VCL.
Краткий теоретический материал
В практических вычислениях довольно часто приходится решать уравнения вида:
(1)
где функция f(x) определена и непрерывна на некотором конечном или бесконечном интервале a < x< b.
Если функция представляет собой многочлен, то уравнение (1) называют алгебраическим, если же в функцию f(x) входят элементарные (тригонометрические, логарифмические, показательные и т. п.) функции, то такое уравнение называют трансцендентным.
Всякое значение x*, обращающее функцию f(x) в нуль, т. е. такое, что
называется корнем уравнения (1), а способ нахождения этого значения x* и есть решение уравнения (1).
Найти корни уравнения вида (1) точно удается лишь в частных случаях. Кроме того, часто уравнение содержит коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней уравнения теряет смысл. Поэтому разработаны методы численного решения уравнений вида (1), которые позволяют отыскать приближенные значения корней этого уравнения.
При этом приходится решать две задачи:
1) отделение корней, т. е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;
2) вычисление корней с заданной точностью.
При выделении областей, в которых находятся действительные корни уравнения (1), можно воспользоваться тем, что если на концах некоторого отрезка непрерывная функция f(x) принимает значения разных знаков, то на этом отрезке уравнение f(x)=0 имеет хотя бы один корень.
Для выделения областей, содержащих один и только один корень, можно воспользоваться, например, графическим способом.
Для решения второй задачи существуют многочисленные методы, из которых мы рассматриваем лишь три: метод итераций, метод Ньютона и метод половинного деления.
При изложении этих методов считаем, что нам известен отрезок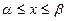 
, внутри которого существует и располагается один и только один из корней уравнения (1).
Задача состоит в нахождении этого корня.
Метод итераций
Уравнение (1) представим в форме:
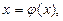(2)
что всегда можно сделать и притом многими способами. Например, можно выделить из уравнения (1) х, остальное перенести в правую часть (это и будет 
). Или умножить левую и правую части (1) на произвольную константу 
и прибавить к левой и правой частям х, т. е. представить (1) в виде
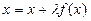
При этом 
.
Выберем на отрезке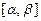 
произвольную точку 
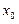- нулевое приближение, и примем в качестве следующего приближения
далее
и вообще пусть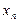 
получается из 
по формуле
. (3)
Этот процесс последовательного вычисления чисел 
по формуле (3) называется методом итераций.
Если на отрезке 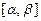, содержащем корень x = x* уравнения (2), а также его последовательные приближения 
вычисляемые по методу итераций, выполнено условие
(4)
то процесс итераций сходится, т. е. увеличивая п,можно получить приближение, сколь угодно мало отличающееся от истинного значения корня х*. Процесс итераций следует продолжать до тех пор, пока для двух последовательных приближений и 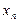не будет обеспечено выполнение неравенства
(5)
при этом всегда будет выполнено неравенство
где 
- заданная предельная абсолютная погрешность корня х*.
Если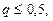 
то 
и вместо (5) можно пользоваться более простым соотношением
(6)
при выполнении которого также будет обеспечена заданная точность определения корня х*.
При практическом нахождении корней по методу итераций нужно при переходе от уравнения (1) к уравнению (2) стремиться представить так, чтобы производная 
по абсолютной величине была возможно меньше 1. В этом случае корень будет всегда найден и чем меньше величина q, тем меньшее число итераций для этого потребуется.
Для приведения уравнения (1) к виду (2) может быть применен достаточно общий прием, обеспечивающий выполнение неравенства (4).
Пусть
(7)
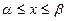при , где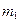 
- наименьшее значение производной 
, а 
- наибольшее значение производной на отрезке .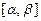
Если производная отрицательна, то вместо уравнения 
рассматриваем уравнение 
.
Заменим уравнение (1) эквивалентным ему уравнением
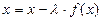
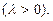
Подберем параметр таким образом, чтобы выполнялось неравенство
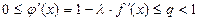при .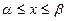
Учитывая условие (7), можно выбрать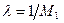 
и 
, при этом условие сходимости метода итераций будет выполнено.
Метод Ньютона
Пусть уравнение имеет один корень на отрезке 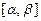, причем и 
определены, непрерывны и сохраняют постоянные знаки на отрезке .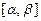
Возьмем некоторую точку 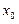отрезка 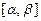и проведем в точке 
графика функции касательную к кривой 
до пересечения с осью Ох. Абсциссу 
точки пересечения можно взять в качестве приближенного значения корня. Проведя касательную через новую точку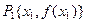 
и находя точку ее пересечения с осью Ox, получим второе приближение корня 
. Аналогично определяются последующие приближения.
Выведем формулу для последовательных приближений к корню. Уравнение касательной, проходящей через точку 
, имеет вид:
Полагая 
, находим абсциссу точки пересечения касательной с осью Ox:
Следующие приближения находим соответственно по формулам:
……………………….. (11)
Процесс вычисления приближений прекратим при выполнении условия
(12)
где 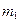- наименьшее значение 
на отрезке ;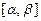 
- наибольшее значение 
на отрезке .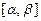
При этом условии будет выполнено неравенство
где - заданная предельная абсолютная погрешность корня 
.
Заметим, что если не больше, чем на два порядка превышает 
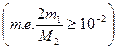, то неравенство (12) заведомо выполняется, если
(13)
Например, при 
в этом случае можно вместо (12) пользоваться более простым условием:
Начальное приближение 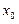целесообразно выбирать так, чтобы было выполнено условие
. (14)
В противном случае сходимость метода Ньютона не гарантируется.
Чаще всего выбирают 
или 
, в зависимости от того, для какой из этих точек выполняется условие (14).
Метод Ньютона эффективен для решения тех уравнений , для которых значение модуля производной близ корня достаточно велико, т. е. график функции 
в окрестности данного корня имеет большую крутизну.
Метод половинного деления
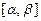Пусть дано уравнение , где функция непрерывна на отрезке и 
.
Если вид функции достаточно сложный, то вычисление функций в методе Ньютона и , необходимой для оценки сходимости в методе итераций, затруднительно. Для решения таких уравнений можно использовать метод половинного деления, который, хотя и требует значительного объема вычислительной работы, но всегда приводит к искомому результату.
Для нахождения корня уравнения (1), принадлежащего отрезку 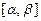, делим отрезок пополам, т. е. выбираем начальное приближение равным 
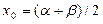. Если 
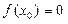, то 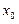является корнем уравнения. Если 
, то выбираем тот из отрезков 
или 
, на концах которого функция имеет противоположные знаки. Полученный отрезок снова делим пополам и проводим то же рассмотрение и т. д.
Процесс деления отрезков пополам продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше наперед заданного числа .
Задание на выполнение работы
Разработать приложение для решения трансцендентного уравнения следующими методами:
· итераций;
· Ньютона;
· половинного деления.
Решение необходимо определить на заданном отрезке с точностью 
. В программе предусмотреть подсчет и вывод на печать числа итераций, за которое удается найти значения корней с заданной точностью.
Вариант 1
Уравнение:
Отрезок, содержащий корень: [2; 3].
Приближенное значение корня: 2,2985.
Проектирование формы показано на рисунке 1.
Краткое описание всех компонентов, которые использовались при разработке приложения, представлено в таблице 1.
Текст программы представлен в приложении А.
Результат выполнения программы представлен в приложении Б.
Рисунок 1. Проектирование формы
Таблица 1- Краткое описание всех компонентов
| Название | Компонент | Назначение |
| «Выполнить» | Button1 | Используется для создания кнопок, которыми пользователь выполняет команды в приложении |
| «» | Edit1 Edit2 Edit3 Edit4 Edit5 Edit6 | Отображение, ввод и редактирование однострочных текстов. Имеется возможность оформления объемного бордюра. Основное свойство - Text |
| «Начало» | Label1 | Отображение текста, который не изменяется пользователем. Никакого оформления текста не предусмотрено, кроме цвета метки и текста. Основное свойство – Caption. |
| «Конец» | Label2 | |
| «Точность вычислений» | Label3 | |
| «Результат» | Label4 | |
| «Количество итераций» | Label5 | |
| «X0» | Label6 |
Продолжение таблицы 1-Краткое описание всех компонентов
| «Отрезок, содержащий корень» | GroupBox1 | Служит для объединения нескольких компонентов с целью удобства пользования программой. |
| «Метод итераций» | RadioButton1 | Предлагают пользователю набор альтернатив, из которого выбирается одна. Набор реализуется требуемым количеством радиокнопок, размещенных в одном контейнере |
| «Метод Ньютона» | RadioButton2 | |
| «Метод половинного деления» | RadioButton3 | |
| «Выбор метода вычислений» | RadioGroup1 | Это панель, которая может содержать регулярно расположенные столбцами и строками радиокнопки. |
Вывод:
1) При выполнении лабораторной работы программно решены уравнения методами итераций, Ньютона и половинного деления с заданной точностью. Выбрано начальное приближение корня из указанного отрезка. В программе предусмотрен подсчет и вывод числа итераций, за которое удается найти значение корня с заданной точностью. Разработан интерфейс приложения с использованием базовых компонентов библиотеки VCL.
2) В ходе лабораторной работы освоены основные методы решения трансцендентных и алгебраических уравнений: метод итераций, метод Ньютона и метод половинного деления в среде визуального программирования Delphi.
Приложение А
Текст программы
(обязательное)
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ExtCtrls;
type
TForm1 = class(TForm)
RadioGroup1: TRadioGroup;
RadioButton1: TRadioButton;
RadioButton2: TRadioButton;
RadioButton3: TRadioButton;
GroupBox1: TGroupBox;
Edit1: TEdit;
Edit2: TEdit;
Label1: TLabel;
Label2: TLabel;
Edit3: TEdit;
Label3: TLabel;
Button1: TButton;
Edit4: TEdit;
Edit5: TEdit;
Label4: TLabel;
Label5: TLabel;
Edit6: TEdit;
Label6: TLabel;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
procedure uravnenie;
var x,x0,a,b,e,z,g,d: real;
n: integer;
function f(x:real):real;
begin
f:=3*sin(sqrt(x))+0.35*x-3.8;
end;
function y(x:real):real;
begin
y:=(3.8-3*sin(sqrt(x)))/0.35;
end;
function y1(x:real):real;
begin
y1:=(3*cos(sqrt(x)))/(0.35*2*sqrt(x));
end;
function f1(x:real):real;
begin
f1:=(3*cos(sqrt(x))/2*sqrt(x))+3.5;
end;
function f2(x:real):real;
begin
f2:=(-3*sin(sqrt(x))-(3*cos(sqrt(x))/sqrt(x)))/4*x;
end;
begin
a:=strtofloat(form1.edit1.text);
b:=strtofloat(form1.Edit2.Text);
e:=strtofloat(form1.edit3.Text);
x0:=strtofloat(form1.Edit6.Text);
if form1.RadioButton1.Checked then
begin
n:=0;
x:=x0;
if y1(x0)<1 then
begin
repeat
z:=y(x);
g:=abs(z-x);
x:=z;
n:=n+1;
until g<e;
form1.Edit4.Text:=floattostr(x);
form1.Edit5.Text:=inttostr(n);
end
else MessageDLG('Условие сходимости не выпонено. Выберите другое значение X0',mtError,[mbOK],0);
end;
if form1.radiobutton2.Checked then
begin
n:=0;
x:=x0;
if f(x0)*f2(x0)>0 then
begin
repeat
z:=x-(f(x)/f1(x));
g:=abs(z-x);
x:=z;
n:=n+1;
until g<e;
form1.Edit4.Text:=floattostr(x);
form1.Edit5.Text:=inttostr(n);
end
else MessageDLG('Условие сходимости не выпонено. Выберите другое значение X0',mtError,[mbOK],0);
end;
if form1.RadioButton3.Checked then
begin
x0:=a; n:=0;
form1.Edit6.Text:=floattostr(x0);
z:=f(a);
repeat
x:=(a+b)/2;
d:=f(x); inc(n);
if d=0 then
exit
else
if z*d<0 then b:=x
else
begin a:=x; z:=d;
end;
until b-a<=e;
form1.Edit4.Text:=floattostr(x);
form1.Edit5.Text:=inttostr(n);
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
uravnenie;
end;
end.
Приложение Б
Результат выполнения программы
(обязательное)
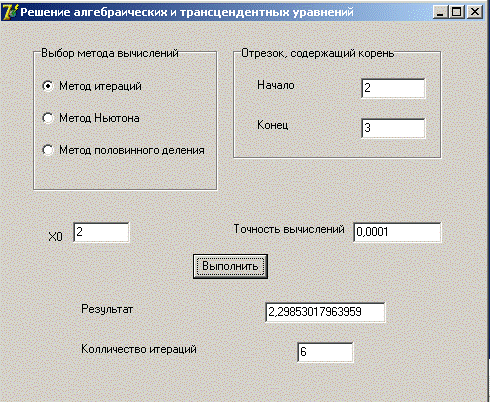
Метод итераций
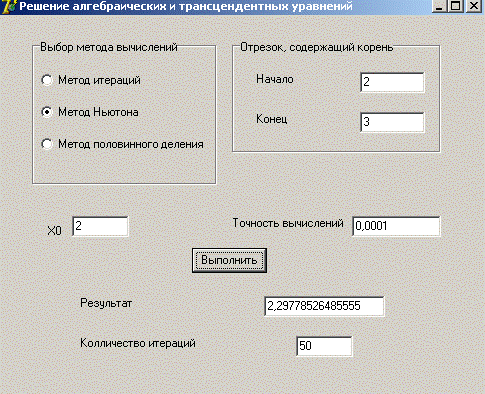
Метод Ньютона
Метод Ньютона-ошибка
Метод половинного деления
