Лекция 1
Введение. Задачи механики, приводящие к системам линейных уравнений
ВВЕДЕНИЕ
Настоящий курс продолжает изучение численных методов, используемых в механике деформируемого твердого тела. Рассмотренные в программе для бакалавров метод конечных элементов и метод конечных разностей позволяют перейти от математической модели конструкций с бесконечным числом степеней свободы к приближенной конечномерной модели. Несмотря на различие в подходах, и метод конечных элементов, и метод конечных разностей, и ряд других методов (метод граничных элементов, метод коллокаций, метод Ритца и т.п.) приводят, как правило, к одному и тому же набору вычислительных задач.
1. Задача статики (определение напряжений и перемещений в конструкции под действием постоянных, не изменяющихся во времени нагрузок) сводится к системе линейных уравнений:
 , (1.1)
, (1.1)
где  ¾ матрица жесткости конструкции;
¾ матрица жесткости конструкции;  ‑ вектор перемещений узловых точек;
‑ вектор перемещений узловых точек;  ‑ вектор внешних сил.
‑ вектор внешних сил.
2. В случае если нагрузки, приложенные к конструкции, вызывают деформации, при которых зависимость напряжений от деформаций перестает быть линейной (напряжения выше предела пропорциональности), задача статики существенно усложняется. В этом случае поведение конструкции описывается уже на системой (1.1), а системой нелинейных уравнений:
 (1.2)
(1.2)
Или, в векторной записи:
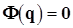 (1.3)
(1.3)
Для задач механики часто возможно сформулировать задачу (1.3) в виде
 , (1.4)
, (1.4)
то есть матрица жесткости не является постоянной, а сама зависит от перемещений.
3. Задача определения частот и форм собственных колебаний конструкции сводится к алгебраической проблеме собственных значений:
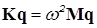 , (1.5)
, (1.5)
4. Задача динамики (поведение конструкции под действием нагрузки, изменяющейся во времени) сводится к системе дифференциальных уравнений:
 . (1.6)
. (1.6)
В первой части курса рассмотрены методы решения систем линейных уравнений (1.1). Подробно рассмотрены прямые методы: метод Гаусса и метод Холецкого. По итерационным методам дана ознакомительная информация.
Во второй части рассмотрены методы решения нелинейных уравнений и систем таких уравнений
Третья часть посвящена методам решения симметричной задачи о собственных значениях (1.5). Метод вращений и степенной метод изложены достаточно полно. О QR-алгоритме, методе Ланцоша и методе итераций в подпространстве приводятся только ознакомительные сведения.
Четвертая часть знакомит читателя с численными методами решения систем обыкновенных дифференциальных уравнений.
ЧАСТЬ 1.
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Системы линейных алгебраических уравнений в задачах механики

Для иллюстрации того, как при решении задач статики получаются системы линейных уравнений, рассмотрим простейшую конструкцию (рис.1.1).
Два груза, последовательно подвешенные на пружинах с жесткостями  и
и  , могут совершать вертикальные перемещения.
, могут совершать вертикальные перемещения. 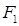 и
и  - силы, приложенные к этим грузам;
- силы, приложенные к этим грузам;  и
и  - перемещения грузов. Используя закон Гука[1], записываем два уравнения равновесия (рис.1.2).
- перемещения грузов. Используя закон Гука[1], записываем два уравнения равновесия (рис.1.2).
В результате получаем систему двух линейных уравнений:
 (1.7)
(1.7)
 Эта система позволяет по известным внешним силам
Эта система позволяет по известным внешним силам 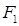 и
и  определить перемещения
определить перемещения  и
и  . Используя матричные обозначения, эту систему можно записать следующим образом:
. Используя матричные обозначения, эту систему можно записать следующим образом:
 , (1.8)
, (1.8)
где
 (1.9)
(1.9)
В программе бакалауреата был рассмотрен метод конечных элементов, который позволяет задачи механики для сплошной деформируемой среды приближенно заменять моделями с конечным числом степеней свободы. Детально этот метод был рассмотрен раньше, здесь напомним только, что согласно этому методу:
1. Непрерывное тело разбивается на отдельные части – конечные элементы.
2. На границах этих элементов выбираются некоторые точки – узлы; перемещения узлов, а иногда (рис 1.3) и повороты, принимаются в качестве основных неизвестных – обобщенных координат.
3. Внешняя распределенная нагрузка заменяется системой эквивалентных сил, приложенных в узлах.
4. Перемещения узловых точек элемента однозначно определяют перемещения его внутренних точек.
5. Следовательно, потенциальная энергия конечных элементов и всей упругой системы однозначно определяется ее узловыми перемещениями.
В линейных задачах (деформации пропорциональны напряжениям) потенциальная энергия представляет собой квадратичную форму:
 , (1.10)
, (1.10)
где 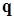 – вектор узловых перемещений (см рис 1.3),
– вектор узловых перемещений (см рис 1.3),  – матрица жесткости системы,
– матрица жесткости системы, 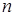 – количество узловых перемещений.
– количество узловых перемещений.
 |
Таким образом, в результате применения метода конечных элементов упругое тело представляется как система с конечным числом степеней свободы (узловых перемещений)
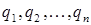 , к узловым точкам которой приложены внешние силы
, к узловым точкам которой приложены внешние силы  .
.
Рис.1.3
Из курса теоретической механики [1.1] известно, что конфигурация механической системы является положением равновесия в том и только в том случае, когда все обобщенные силы равны нулю. В данном случае эти силы будут складываться из потенциальных сил  и внешних сил
и внешних сил  , следовательно, условия равновесия системы:
, следовательно, условия равновесия системы:
 . (1.11)
. (1.11)
Учитывая симметрию матрицы жесткости  , для производной потенциальной энергии получаем
, для производной потенциальной энергии получаем
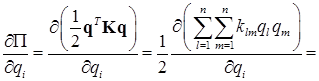
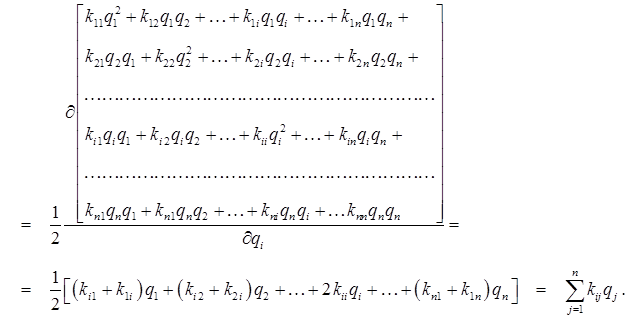 (1.12)
(1.12)
Подставляя (1.12) в (1.11), получаем
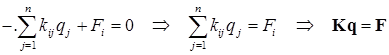 . (1.13)
. (1.13)
К системе вида (1.13) сводятся задачи статики и при использовании многих других методов дискретизации непрерывной задачи: метода конечных разностей, метода граничных элементов, метода Ритца.

Система уравнений (1.13) была получена при предположении о линейной зависимости напряжений и деформаций. Однако при решении задач с нелинейным поведением материала также, как правило, возникает необходимость решения систем линейных уравнений. При этом решение нелинейной задачи находится в результате решения последовательности линейных задач.
Действительная кривая 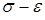 материала заменяется ломаной (секущие модули на рис. 1.4, б). В пределах каждого отрезка поведение материала считается линейным. Другой вариант (касательные модули на рис. 1.4, а) также рассматривает поведение материала как линейное в пределах малого диапазона деформаций. В этом случае в качестве модуля упругости принимается тангенс угла наклона касательной к диаграмме при данной деформации.
материала заменяется ломаной (секущие модули на рис. 1.4, б). В пределах каждого отрезка поведение материала считается линейным. Другой вариант (касательные модули на рис. 1.4, а) также рассматривает поведение материала как линейное в пределах малого диапазона деформаций. В этом случае в качестве модуля упругости принимается тангенс угла наклона касательной к диаграмме при данной деформации.
В обоих случаях расчет проводится методом последовательных приближений. Сначала как для обычной линейной задачи строится и решается система уравнений:
 . (1.14)
. (1.14)
Полученное первое приближение  позволяет, используя полученные значения деформаций в элементах, уточнить в соответствии с диаграммой
позволяет, используя полученные значения деформаций в элементах, уточнить в соответствии с диаграммой 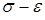 значение модуля упругости для каждого элемента и построить матрицу жесткости второго приближения
значение модуля упругости для каждого элемента и построить матрицу жесткости второго приближения  . Вновь решается система
. Вновь решается система
 . (1.15)
. (1.15)
Полученное решение вновь используется для уточнения матрицы жесткости. Этот процесс продолжается до достижения сходимости.
Замечание. Здесь кратко описана процедура, представляющая один из вариантов метода простых итераций. Подробнее вопрос о методах решения систем нелинейных уравнений будет рассмотрен во второй части курса.
Таким образом, важность систем линейных уравнений в задачах механики установлена. Переходим к методам, используемым для ее решения.
Литература
1. Гантмахер Ф.Р. Лекции по аналитической механике. – М.: Наука, 1966. – 300с.
[1] Гук Роберт (1635-1703) – английский естествоиспытатель, разносторонний ученый и экспериментатор, архитектор.






