Высшего образования
«Сибирский федеральный университет»
ИНСТИТУТ ГОРНОГО ДЕЛА, ГЕОЛОГИИ И ГЕОТЕХНОЛОГИЙ
МАТЕМАТИКА
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Для студентов-заочников специальностей
21.05.04 «Горное дело»
Горные машины и оборудование
Электрификация и автоматизация горного производства
Открытые горные работы
Семестра
Федеральное государственное автономное
образовательное учреждение
Высшего образования
«Сибирский федеральный университет»
ИНСТИТУТ ГОРНОГО ДЕЛА, ГЕОЛОГИИ И ГЕОТЕХНОЛОГИЙ
МАТЕМАТИКА
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Для студентов-заочников специальностей
21.05.04 «Горное дело»
Семестра
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Ниже приведены таблицы номеров задач, входящих в задания на контрольные работы, по учебным планам. Студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой его номера студенческого билета (шифр).
.
Студенты, изучающие математику 4 семестра, выполняют:
Контрольные работы № 1 (1 семестр).
Контрольные работы № 2 (2 семестр).
Контрольные работы № 3 (3 семестр).
Контрольные работы № 4 (4 семестр).
| Вариант | Контрольная работа №1 | |||||||
| Вариант | Контрольная работа №2 | |||||||
| Вариант | Контрольная работа №3 | |||
| Вариант | Контрольная работа №4 | |||
Элементы векторной алгебры
И аналитической геометрии
11 – 20. Даны координаты вершин пирамиды А 1 А 2 А 3 А 4. Найти:
1) длину ребра А 1 А 2; 2) угол между ребрами А 1 А 2 и А 1 А 4; 3) угол между ребром А 1 А 4 и гранью А 1 А 2 А 3; 4) площадь грани А 1 А 2 А 3; 5) объем пирамиды; 6) уравнение прямой А 1 А 2; 7) уравнение плоскости А 1 А 2 А 3; 8) уравнение высоты, опущенной из вершины А 4 на грань А 1 А 2 А 3. Сделать чертеж.
11. А 1 (2; 1; –4), А 2(1; –2; 3), А 3(1; –2; –3), А 4(5; –2; 1).
12. А 1 (2; –1; 3), А 2 (–5; 1; 1), А 3(0; 3; –4), А 4(–1; –3; 4).
13. А 1 (5; 3; 6), А 2 (–3; –4; 4), А 3(5; –6;8), А 4(4; 0; –3).
14. А 1 (5; 2; 4), А 2(–3; 5; –7), А 3(1; –5; 8), А 4(9; –3; 5).
15. А 1 (7; –1; –2), А 2(1; 7; 8), А 3(3; 7; 9), А 4(–3; –5; 2).
16. А 1 (–2; 3; 4), А 2(4; 2; –1), А 3(2; –1; 4), А 4(–1; –1; 1).
17. А 1 (0; 4; –4), А 2(5; 1; –1), А 3(–1; –1; 3), А 4(0; –3; 7).
18. А 1 (0; –6; 3), А 2(3; 3; –3), А 3(–3; –5; 2), А 4(–1; –4; 0).
19. А 1 (2; –1; 3), А 2(–5; 1; 1), А 3(0; 3; –4), А 4(–1; –3; 4).
20. А 1 (2; 1; –4), А 2(1; –2; 3), А 3(1; –2; –3), А 4(5; –2; 1).
31 – 40. Привести уравнение кривой второго порядка к каноническому виду, построить график кривой.
31. x 2 + у 2 – 4 x + 2 у = 4; 32. x 2 – у 2 – 4 у – 13 = 0;
33. x 2 – 4 x + 2 у + 2= 0; 34. x 2 + 4 x + 4 у 2 + 8у – 5 = 0;
35. x 2 – 6 у 2 – 12 x + 36 у – 54 = 0; 36. 2 x 2 + 4 x + 18 у 2 – 16= 0;
37. 2 x 2 + 2 у 2+ 4 x – 8 у – 8 = 0; 38. – x + у 2 + 2 у = 0;
39. 3 x 2 + 5 у 2 + 12 x – 10 у + 2 = 0; 40. 4 x 2 – 3 у 2 – 8 x – 6 у – 11 = 0.
Элементы линейной алгебры
51 – 60. Дана система линейных уравнений

Доказать ее совместность и решить двумя способами: 1) по формулам Крамера; 2) методом Гаусса:
| 51. | 
| 52. | 
|
| 53. | 
| 54. | 
|
| 55. | 
| 56. | 
|
| 57. | 
| 58. | 
|
| 59. | 
| 60. | 
|
71 – 80. Дано комплексное число z. Требуется: 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w 3 + z = 0.
| 71. | 
| 72. | 
| 73. | 
|
| 74. | 
| 75. | 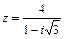
| 76. | 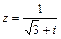
|
| 77. | 
| 78. | 
| 79. | 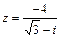
|
| 80. | 
|
Введение в математический анализ
91 – 100. Найти пределы функций, не пользуясь правилом Лопиталя.
91. a) 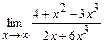 ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
92. a)  ; б)
; б)  ;
;
в)  ; г)
; г) 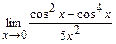 ; д)
; д) 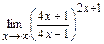 .
.
93. a) 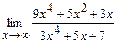 ; б)
; б)  ;
;
в)  ; г)
; г)  ; д).
; д). 
94. a)  ; б)
; б) 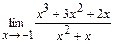 ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
95. a)  ; б)
; б)  ;
;
в) 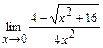 ; г)
; г)  ; д)
; д)  .
.
96. a)  ; б)
; б)  .
.
в)  ; г)
; г)  ; д)
; д) 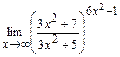 .
.
97. a) 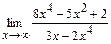 ; б)
; б)  ;
;
в)  ; г)
; г) 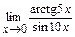 ; д)
; д) 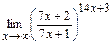 .
.
98. a) 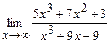 ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д) 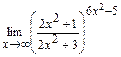 .
.
99. a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
100. a)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
4. Производная и еЁ приложения
121 - 130. Найти производные  данных функций.
данных функций.
| 121. | a)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
| |
д)  . .
| ||
| 122. | а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
| |
д)  . .
| ||
| 123. | а) 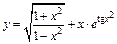 ; ;
| б)  ; ;
|
в)  ; ;
| г) 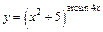 ; ;
| |
д)  . .
| ||
| 124. | а)  ; ;
| б)  ; ;
|
в) 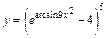 ; ;
| г)  ; ;
| |
д)  . .
| ||
| 125. | а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
| |
д)  . .
| ||
| 126. | а)  ; ;
| б) 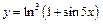 ; ;
|
в)  ; ;
| г)  ; ;
| |
д)  . .
| ||
| 127. | а)  ; ;
| б)  ; ;
|
в) 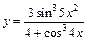 ; ;
| г) 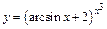 ; ;
| |
д) 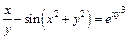 . .
| ||
| 128. | а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
| |
д)  . .
| ||
| 129. | а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
| |
д)  . .
| ||
| 130. | а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
| |
д)  . .
|
5. Приложения дифференциального
Исчисления
151 – 160. Исследовать методами дифференциального исчисления функцию  и, используя полученные результаты, построить её график.
и, используя полученные результаты, построить её график.
151. 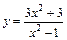 . 152.
. 152.  .
.
153.  . 154.
. 154.  .
.
155.  . 156.
. 156. 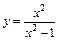 .
.
157.  . 158.
. 158.  .
.
159.  . 160.
. 160.  .
.
6. Дифференциальное исчисление функций
Нескольких переменных
161 – 170. Найти а)  ; б)
; б)  .
.
| 161. | a)  , ,
| б)  . .
|
| 162. | а)  , ,
| б)  . .
|
| 163. | а)  ; ;
| б)  . .
|
| 164. | а)  ; ;
| б)  . .
|
| 165. | а) 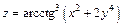 ; ;
| б)  . .
|
| 166. | а)  ; ;
| б)  . .
|
| 167. | а)  ; ;
| б)  . .
|
| 168. | а)  ; ;
| б)  . .
|
| 169. | а)  ; ;
| б)  . .
|
| 170. | а) 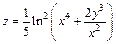 ; ;
| б)  . .
|
191 – 200. Даны функция  , точка
, точка  и вектор
и вектор  . Найти: 1) grad z в точке А; 2) производную в точке А по направлению вектора
. Найти: 1) grad z в точке А; 2) производную в точке А по направлению вектора 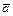 .
.
191. 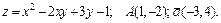
192. 
193. 
194. 
195. 
196. 
197. 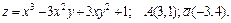
198. 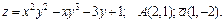
199. 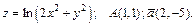
200. 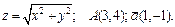
7. НеопределЁнный и определЁнный
Интегралы
201 – 210. Найти неопределенные интегралы. В пп. «а» и «б» результаты проверить дифференцированием.
| 201. | a) 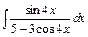 ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
| |
д)  ; ;
| е)  . .
| |
| 202. | a) 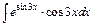 ; ;
| б)  ; ;
|
в)  ; ;
| г) 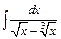 ; ;
| |
д)  ; ;
| е)  . .
| |
| 203. | a)  ; ;
| б)  ; ;
|
в)  ; ;
| г) 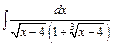 ; ;
| |
д)  ; ;
| е)  . .
| |
| 204. | a)  ; ;
| б) 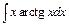 ; ;
|
в)  ; ;
| г)  ; ;
| |
д)  ; ;
| е)  . .
| |
| 205. | a)  ; ;
| б) 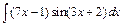 ; ;
|
в)  ; ;
| г)  ; ;
| |
д)  ; ;
| е)  . .
| |
| 206. | a) 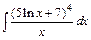 ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
| |
д) 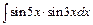 ; ;
| е) 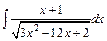 . .
| |
| 207. | a)  ; ;
| б)  ; ;
|
в)  ; ;
| г) 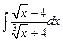 ; ;
| |
д)  ; ;
| е) 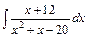 . .
| |
| 208. | a) 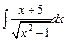 ; ;
| б)  ; ;
|
в) 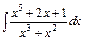 ; ;
| г)  ; ;
| |
д)  ; ;
| е)  . .
| |
| 209. | a) 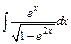 ; ;
| б)  ; ;
|
в) 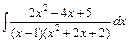 ; ;
| г)  ; ;
| |
д)  ; ;
| е)  . .
| |
| 210. | a)  ; ;
| б)  ; ;
|
в) 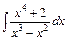 ; ;
| г) 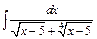 ; ;
| |
д)  ; ;
| е)  . .
|
211 – 220. Вычислить несобственный интеграл или доказать его расходимость.
| 211. | а) 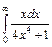 ; ;
| б).  . .
|
| 212. | а)  ; ;
| б).  . .
|
| 213. | а)  ; ;
| б). 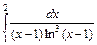 . .
|
| 214. | а)  ; ;
| б).  . .
|
| 215. | а) 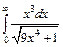 ; ;
| б).  . .
|
| 216. | а)  ; ;
| б). 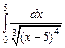 . .
|
| 217. | а)  ; ;
| б).  . .
|
| 218. | а)  ; ;
| б).  . .
|
| 219. | а) 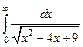 ; ;
| . б). 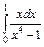 . .
|
| 220. | а)  ; ;
| б).  . .
|
Дифференциальные уравнения
231 – 240. Найти общее решение дифференциального уравнения.
| 231. | а)  ; ;
| б) 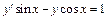 . .
|
| 232. | а)  ; ;
| б)  . .
|
| 233. | а) 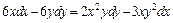 ; ;
| б)  . .
|
| 234. | а)  ; ;
| б) 
|
| 235. | а) 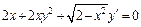 ; ;
| б) 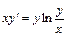 . .
|
| 236. | а)  ; ;
| б) 
|
| 237. | а)  ; ;
| б)  . .
|
| 238. | а)  ; ;
| б)  . .
|
| 239. | а)  ; ;
| б)  . .
|
| 240. | а)  . .
| б)  . .
|
251 – 260. Найти частное решение дифференциального уравнения  , удовлетворяющее начальным условиям y (0) = y 0,
, удовлетворяющее начальным условиям y (0) = y 0,
y' (0)= y' 0. (Задача Коша).
251. y'' – y'  ;
;  ,
,  .
.
252. y'' + y  ; y (0) = 4;
; y (0) = 4;  ;
;
253. y'' +7 y' +12 y =  ; y (0) = 1, y' (0) = 1;
; y (0) = 1, y' (0) = 1;
254. y'' –2 y' = x 2–1; y (0) = 1, y' (0) = 1;
255. y''-  ; y (0) = 1, y' (0) = 1.
; y (0) = 1, y' (0) = 1.
256. y'' + 9 y  y (0) =
y (0) =  ; y' (0) = 0.
; y' (0) = 0.
257. y'' – 4 y' +8 y  ; y (0) = 2, y' (0) = 3.
; y (0) = 2, y' (0) = 3.
258. y'' – 2 y' =  ; y (0) = 2, y' (0) = 2.
; y (0) = 2, y' (0) = 2.
259. y '' +2 y ' +10 y  ; y (0) = 0, y' (0) =
; y (0) = 0, y' (0) = 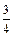 .
.
260. y'' – 6 y' +9 y =  ; y (0)=1, y' (0)=3.
; y (0)=1, y' (0)=3.
9. Кратные, криволинейные
И поверхностные интегралы
281 – 290. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость xOy.
| 281. | 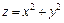 ; ;
| 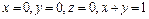 . .
|
| 282. | 
|  . .
|
| 283. |  , ,
|  . .
|
| 284. |  , ,
|  . .
|
| 285. |  , ,
|  . .
|
| 286. | 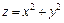 , ,
|  . .
|
| 287. | 
|  . .
|
| 288. |  , ,
| 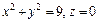 . .
|
| 289. |  , ,
|  . .
|
| 290. |  , ,
| 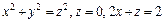 . .
|
Ряды
301 – 310. Исследовать сходимость числового ряда 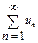 .
.
301.  ; 302.
; 302.  .
.
303.  ; 304.
; 304. 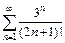 .
.
305.  ; 306.
; 306. 
307.  ; 308.
; 308.  .
.
309.  ; 310.
; 310.  .
.
311–320. Найти область сходимости ряда.
311.  ; 312.
; 312.  .
.
313.  ; 314.
; 314.  .
.
315.  ; 316.
; 316. 
317.  ; 318.
; 318. 
319.  ; 320.
; 320.  .
.
331 – 340. Найти три первых, отличных от нуля, члена разложения в степенной ряд решения  дифференциального уравнения
дифференциального уравнения  , удовлетворяющего начальному условию
, удовлетворяющего начальному условию  .
.
| 331. |  . .
| 332. | 
|
| 333. | 
| 334. | 
|
| 335. | 
| 336. | 
|
| 337. | 
| 338. | 
|
| 339. | 
| 340. | 
|
341 – 350. Разложить данную функцию f (x) в ряд Фурье в интервале [ a; b ].
| 341. | 
| 342. | 
|
| 343. | 
| 344. | 
|
| 345. | 
| 346. | 
|
| 347. | 
| 348. | 
|
| 349. | 
| 350. | 
|
Теория вероятностей






