ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ
Режимы движения жидкости
Одна из основных задач практической гидравлики − оценка потерь напора на преодоление гидравлических сопротивлений, возникающих при движении реальных жидкостей в различных гидравлических системах. Точный учет этих потерь во многом определяет надежность технических расчетов.
Рисунок 31 – Схема установки Рейнольдса
Рейнольдс пропускал жидкость из бака Б, в котором с помощью перелива 7 поддерживался постоянный уровень, через стеклянные трубки различного диаметра, регулируя скорость движения жидкости в них кранами 1 и 5. По тонкой трубке 3 с заостренным концом ко входу в стеклянную трубку 4 подводилась окрашенная жидкость из сосуда 2. Средняя скорость V в трубке 4, имеющей площадь живого сечения ω, определялась по объему жидкости W, поступившей в мерный сосуд 6 за время t (рис. 31).
Как показывают исследования, структура потока при различных скоростях течения различна.
При малых скоростях течения в потоке жидкости появляются окрашенные струйки. Они движутся прямолинейно, без пульсаций, не перемешиваясь с соседними слоями жидкости (рис. 31а). Такое параллельно-струйное спокойное движение жидкости без поперечного перемешивания и при отсутствии пульсации скорости и давления называют ламинарным (слоистым) режимом движения жидкости.
При постепенном увеличении скорости движения жидкости при некоторой скорости течения параллельно-струйное движение нарушится, окрашенные струйки станут пульсирующими, появятся разрывы. А при дальнейшем увеличении скорости окрашенные струйки исчезнут, перемешавшись с потоком жидкости (рис. 31б). Движение станет беспорядочным вследствие пульсации скоростей и давления, что и приводит к перемешиванию частиц жидкости. Движение жидкости, во время которого происходит пульсация скоростей и давления, называют турбулентным (беспорядочным) режимом движения.
Обобщив результаты своих опытов, Рейнольдс нашел общие условия, при которых возможны существование того или иного режима или переход одного режима к другому. Он установил, что основными факторами, определяющими характер режима, являются: средняя скорость движения жидкости V, внутренний диаметр трубы d, плотность жидкости ρ и динамическая вязкость η.
Для характеристики режима движения Рейнольдс ввел безразмерный параметр Re, учитывающий влияние перечисленных факторов, называемый числом (или критерием) Рейнольдса.
Re=Vdρ/η, но η/ρ=ν, тогда Re=Vd/ν.
Границы существования того или иного режима движения жидкости определяются двумя числами Рейнольдса, которые называются критическими: нижним ReKр.H .=2320 и верхним ReKp.B. =13800 (сам Рейнольдс получил несколько иные значения ReKр.H .=2000 ReKp.B .=12000). Значения скоростей, соответствующие этим значениям числа Рейнольдса, также называют критическими (нижней критической Vh.k . и верхней критической Vb.k .).
Таким образом, при Re<ReKр.H. (соответственно V<Vh.k.) возможен только ламинарный режим, при Re>ReKp.B. (V>VВ.К.) − турбулентный, а при ReKp.H.<Re<ReKp.В ., или VН.К.<V<VВ.К.) наблюдается неустойчивое состояние потока.
Тогда для определения характера режима движения жидкости необходимо в каждом отдельном случае вычислять число Рейнольдса Re=Vd/ν и сравнивать результат с критическими значениями.
В настоящее время при расчетах принято исходить только из нижнего значения критического числа Рейнольдса ReКp .=2320 и считать режим ламинарным при Re <2320, а турбулентным при Re >2320. При этом движение в неустойчивой зоне исключается из рассмотрения, что приводит к некоторому запасу и большей надежности в гидравлических расчетах.
С физической точки зрения критерий Re есть отношение сил инерции потока к силам трения при его движении.
Определение режима движения жидкости в практических расчетах имеет очень важное значение. Опыты показали, что потери напора по длине потока при ламинарном режиме движения пропорциональны средней скорости в первой степени:
hω=kлV,
где hω − потери напора по длине потока;
кл − коэффициент пропорциональности;
V − средняя скорость течения потока.
Для турбулентного режима движения потери напора по длине потока пропорциональны средней скорости в степени n:
hω=kлVn,
где n – показатель степени, изменяющийся от 1,75 до 2.
Покажем на графике (рис. 32) соотношение между потерями напора hω и числом Re. Как видно, с увеличением числа Рейнольдса показатель степени увеличивается. При развитой турбулентности n =2. Следовательно, при определении потерь напора надо знать характер режима движения, а затем уже выбрать соответствующую формулу для определения потерь напора.
Рисунок 32 Зависимость hω=f(Re)
Особенности течения при ламинарном режиме
Ламинарный режим характерен четким выделением отдельных струек. Рассмотрим распределение касательных напряжений, давления, скоростей при ламинарном режиме (рис. 33).
Рисунок 33 – Распределение касательных напряжений, давлений и скоростей по живому сечению при ламинарном режиме
Касательные напряжения. Касательное напряжение τ на произвольном удалении r от центра трубы можно записать из основного уравнения равномерного движения.
,
где I – гидравлический уклон, равный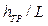 
;
R – гидравлический радиус, равный 
.
В соответствии с уравнением Бернулли гидравлический уклон для всех струек одинаков. Следовательно, касательные напряжения будут изменяться линейно. Максимальное значение τ у стенок трубы в прилипшем слое при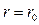 
, а на оси при r =0, τ =0.
Распределение давления. В этом случае действует закон статики, поэтому распределение давления происходит по гидростатическому закону. Наибольшее давление будет в точке С у нижней кромки трубы pC=pA +2 γr 0, причем часто разницей давления по сечению трубы можно пренебречь и считать во всех точках его равным давлению в центре тяжести сечения на оси трубы.
Распределение скоростей. Касательные напряжения при ламинарном режиме можно выразить из закона вязкого трения Ньютона:
.
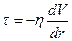Приравняем два выражения
.
Из этого выражения, произведя преобразования и интегрирование, получим скорость:
.
Постоянную интегрирования C, определим из условий нулевой скорости на стенках трубы (U= 0при r= 0), откуда
.
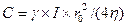Окончательно закон распределения скоростей имеет вид
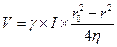; при r= 0; 
Эпюра скоростей в живом сечении представляет собой парабалоид вращения. Скорость изменяется от нуля в прилипшем слое у стенок трубы до Vmax на оси.
Расход и средняя скорость. Элементарный расход в живом кольцевом сечении толщиной dr и удаленном от центра на расстояние r можно выразить по формуле:
.
Проинтегрировав это выражение от 0 до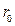 
, получим расход потока жидкости:
.
Среднюю скорость определим из уравнения неразрывности 
, где 
, тогда:
.
Сопоставив выражения для расчета максимальной скорости Vmax и средней скорости отметим, что они связаны соотношением: 
, с учетом этого соотношения закон распределения скоростей можно записать так:
.
Потери энергии (напора) и коэффициент Дарси. Формулу для определения потерь энергии на трение в круглой трубе можно получить, преобразовав формулу для расчета средней скорости, выразив в ней гидравлический уклон как 
, тогда
(формула Пуазейля).
В общем случае потери энергии на трение выражается формулой Дарси-Вейсбаха:
hТР=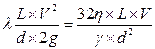 
.
С учетом известных соотношений: ν=η/ρ, γ=ρ×ν, Re=V×d/ν получим значение коэффициента Дарси для ламинарного режима:
λ =64/ Re.
Анализируя формулу, можно сделать вывод о линейной зависимости коэффициента Дарси λ от числа Рейнольдса Re, а также о такой же зависимости потерь на трение (по длине) hТР от средней скорости V.
