ЛЕКЦИЯ № 2
СИСТЕМЫ СЧИСЛЕНИЯ И ПРЕДСТАВЛЕНИЕ
ИНФОРМАЦИИ В ЭВМ
Понятие об основных системах счисления
Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами. Все системы счисления делятся на позиционные и непозиционные.
Непозиционными называются такие системы счисления, в которых каждый символ сохраняет свое значение независимо от места его положения в числе. Примером непозиционной системы счисления является римская система, в которой символам I, V, X, L, С, D, М соответствуют числа 1, 5, 10, 50, 100, 500, 1000. Недостатком этой системы является сложность формальных правил записи чисел и выполнения арифметических действий над ними.
Система счисления называется позиционной, если значение каждого знака в числе зависит от позиции, которую занимает знак в записи числа. Это значение находится в однозначной зависимости от позиции, занимаемой цифрой, по некоторому закону. Примером позиционной системы счисления является десятичная система, используемая в повседневной жизни.
Количество различных цифр, употребляемых в позиционной системе, определяет название системы счисления и называется основанием системы счисления. Так, в десятичной системе используются десять цифр (от 0 до 9), основанием этой системы является число десять.
В позиционных системах счисления числа записываются в виде последовательности символов:
N = an an-1... a1 a0, a-1 a-2... а-m (р) (1)
где N – число; ai – цифры (символы) числа; p – основание системы счисления; n, m – порядковый номер разряда для целой (n) и дробной (m) частей числа соответственно.
В этой последовательности запятая отделяет целую часть числа от дробной (коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях). Значение числа, записанного в виде (1), может быть найдено по следующей формуле:
N = an · pn+an-1 · pn-1+... +a0 · p0+a-1 · p-1+a-2 · p-2+...+а-m · p-m. (2)
В десятичной системе счисления мы производим вычисления по формуле (2) практически не задумываясь. Возьмём для примера десятичное число 123,45:
2 1 0 -1 -2
123,45 (10) = 1·102+2·101+3·100+4·10-1+5·10-2 = 100+20+3+0,4+0,05.
Помимо десятичной, в ЭВМ применяются и другие позиционные системы счисления: двоичная, восьмеричная, шестнадцатеричная.
Двоичная система счисления.
Используется две цифры: 0 и 1. Особая значимость двоичной системы счисления в информатике определяется тем, что внутреннее представление любой информации в компьютере является двоичным кодом. Примеры представления чисел в двоичной системе счисления представлены в таблице 1.
Восьмеричная система счисления.
Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употреблялась в ЭВМ первого и второго поколений как вспомогательная для записи адресов и данных в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (табл. 1). Триада получается путем добавления, при необходимости, незначащих нулей.
Таблица 1
Представление чисел в различных системах счисления
| Десятичная (Основание 10) | Римская | Двоичная (основание 2) | Восьмеричная (Основание 8) | Двоичная (триады) | Шестнадцатеричная (Основание 16) | Двоичная (тетрады) |
| I | ||||||
| II | ||||||
| III | ||||||
| IV | ||||||
| V | ||||||
| VI | ||||||
| VII | ||||||
| VIII | 001 000 | |||||
| IX | 001 001 | |||||
| X | 001 010 | A | ||||
| XI | 001 011 | B | ||||
| XII | 001 100 | C | ||||
| XIII | 001 101 | D | ||||
| XIV | 001 110 | E | ||||
| XV | 001 111 | F | ||||
| XVI | 010 000 | 0001 0000 | ||||
| XVII | 010 001 | 0001 0001 |
Шестнадцатеричная система счисления.
Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр - латинскими буквами: 10-A, 11-B, 12-C, 13-D, 14-E, 15-F. Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада, или полубайт) (табл. 1).
Перевод чисел из одной системы счисления в другую
Перевод чисел в десятичную систему осуществляется путем составления степенного ряда (2) с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.
Пример.
а) Перевести 10101101,101(2) в десятичную систему счисления
10101101,101(2) = 1·27 + 0·26 + 1·25 + 0·24 + 1·23 + 1·22 + 0·21 + 1·20 + 1·2-1 + + 0·2-2 + 1·2-3 = 173,625(10)
б) Перевести 703,04(8) в десятичную систему счисления
703,04(8) = 7·82 + 0·81 + 3·80+ 0·8-1 + 4·8-2 = 451,0625(10)
в) Перевести B2E,4(16) в десятичную систему счисления
B2E,4(16) = 11·162 + 2·161 + 14·160 + 4·16-1 = 2862,25(10)
Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основании той системы, в которую оно переводится, до тех пор, пока не получится частное, меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.
Пример.
а) Перевести 181(10) в восьмеричную систему счисления
| _181 | ||
| _22 | ||

|
Результат: 181(10) = 265(8)
б) Перевести 622(10) в шестнадцатеричную систему счисления
| _622 | ||
| _38 | ||
| _142 | ||
 6 6
| ||
Результат: 622(10) = 26E(16)
Перевод правильных дробей из десятичной системы счисления в недесятичную. Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Пример.
Перевести 0,3125(10) в восьмеричную систему счисления
 0, 3125 0, 3125
| ´ | ||
| ´ | |||
Результат: 0,3125(10) = 0,24(8)
Замечание. Конечной десятичной дроби может соответствовать бесконечная (периодическая) дробь в недесятичной системе счисления. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Пример.
Перевести 0,65(10) в двоичную систему счисления с точностью до 6 знаков после запятой.
 0, 65 0, 65
| ´ | ||
| ´ | |||
| ´ | |||
| ´ | |||
| ´ | |||
| ´ | |||
| ´ | |||
| ... |
Результат: 0,65(10) ≈ 0,101001 (2)
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Пример.
Перевести 23,125(10) в двоичную систему счисления
1) Переведем целую часть:
| _ | |||||
| _11 | |||||
| _5 | |||||

| _2 | ||||
2) Переведем дробную часть:
| 0, 125 | ´ | ||
 0 0
| ´ | ||
| ´ | |||
Таким образом: 0,125(10) = 0,001(2); 23(10) = 101112.
Результат: 23,125(10) = 10111,001(2).
Необходимо отметить, что целые числа остаются целыми, а правильные дроби — дробями в любой системе счисления.
Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) – для восьмеричной системы счисления или четырехразрядным двоичным числом (тетрадой) – для шестнадцатеричной системы счисления (табл. 1), после чего отбрасывают незначащие нули в старших и младших разрядах.
Пример.
а) Перевести 305,4(8) в двоичную систему счисления
 3 3
| 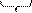 0 0
| 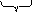 5 5
| , | 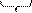 4 4
| (8) | = 11000101,1(2) |
б) Перевести 7B2,E(16) в двоичную систему счисления
 7 7
| 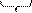 В В
| 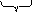 2 2
| , | 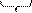 Е Е
| (16) | = 11110110010,111(2) |
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от десятичной точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой (табл. 1).
Пример.
а) Перевести 1101111001,1101(2) в восьмеричную систему счисления
 001 001
| 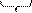 101 101
| 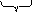 111 111
| 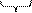 001 001
| , | 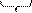 110 110
| 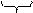 100 100
| = 1571,64(8) |
б) Перевести 11111111011,100111(2) в шестнадцатеричную систему счисления
 0111 0111
|  1111 1111
|  1011 1011
| , |  1001 1001
|  1100 1100
| = 7FB,9C(16) |
| F | B | С |
Перевод из восьмеричной в шестнадцатеричную систему и обратно удобно осуществлять через двоичную систему с помощью триад и тетрад.
Пример.
Перевести 175,24(8) в шестнадцатеричную систему счисления
 1 1
| 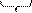 7 7
| 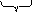 5 5
| , | 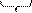 2 2
| 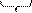 4 4
| (8) |    = 1111101,0101(2) = 0111 1101, 0101 (2) = 7D,5(16) = 1111101,0101(2) = 0111 1101, 0101 (2) = 7D,5(16)
|
| 7 D 5 |
ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ЭВМ
Основы алгебры логики
Слово «логика» означает как совокупность правил, которым подчиняется процесс мышления, так и науку о правилах рассуждений. Логика, как наука о законах и формах мышления, изучает абстрактное мышление как средство познания объективного мира.
Основными формами абстрактного мышления являются:
— ПОНЯТИЯ,
— СУЖДЕНИЯ,
— УМОЗАКЛЮЧЕНИЯ.
ПОНЯТИЕ — форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов, например: «портфель»; «трапеция»; «ветер».
СУЖДЕНИЕ — мысль, в которой что-либо утверждается или отрицается о предметах. Суждения являются истинными или ложными повествовательными предложениями. Они могут быть простыми и сложными. Например: «Весна наступила»; «Грачи прилетели»; «Весна наступила, и грачи прилетели».
УМОЗАКЛЮЧЕНИЕ — прием мышления, посредством которого из исходного знания получается новое знание; из одного или нескольких истинных суждений, называемых посылками, мы по определенным правилам вывода получаем заключение.
Все металлы — простые вещества.
Литий — металл.
Литий — простое вещество.
Чтобы достичь истины при помощи умозаключений, надо соблюдать законы логики. Существует формальная и математическая логика.
Формальная логика — наука о законах и формах мышления.
Математическая логика изучает логические связи и отношения, лежащие в основе дедуктивного (логического) вывода.
Формальная логика связана с анализом наших обычных содержательных умозаключений, выражаемых разговорным языком. Математическая логика изучает только умозаключения со строго определенными объектами и суждениями, для которых можно однозначно решить, истинны они или ложны.
В основе логических схем и устройств ЭВМ лежит специальный аппарат, использующий законы математической логики. Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем. Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции.
Алгебра логики — это раздел математической логики, значения всех элементов (функций и аргументов) которой определены в двухэлементном множестве: «Истина» («True») и «Ложь» («False»), или 1 и 0.
В математической логике суждения называются высказываниями. Алгебру логики иначе называют алгеброй высказываний.
Высказывание — это повествовательное предложение, о котором можно сказать, истинно оно или ложно.
Примеры высказываний:
Сейчас идет снег. может быть истинным или ложным
Земля — планета Солнечной системы. истинно
2 + 8 < 5 ложно
5 * 5 = 25 истинно
Всякий квадрат есть параллелограмм. истинно
Всякий параллелограмм есть квадрат. ложно
2 * 2 = 5 ложно
А вот примеры, не являющиеся высказываниями: «Уходя, гасите свет!»; «Да здравствует мыло душистое и полотенце пушистое!»
Высказывания, приведенные выше, являются простыми. Сложные высказывания получаются путем объединения простых высказываний связками — союзами И, ИЛИ и частицей НЕ. Значение истинности сложных высказываний зависит от истинности входящих в них простых высказываний и от объединяющих их связок.
Операции сравнения
Операции сравнения называют еще операциями отношения (relation operations), поскольку в них осуществляется оценка взаимосвязи (отношений) двух операндов. Под операндом понимается то, над чем выполняется операция.
В таблице 6 перечислены операторы, используемые для обозначения операций сравнения в языках программирования. Результат сравне-ния может быть либо истинным, либо ложным (Тruе или False). Приоритет операций сравнения ниже, чем у арифметических операций.
Таблица 2






