Погрешности средств измерений

Погрешность средств измерений (инструментальная) является одной из составляющих погрешности измерений и имеет определяющее значение для наиболее распространенных технических измерений.

На рис. 2.6 приведена классификация погрешностей средств измерений по ряду признаков, которые далее рассмотрены подробнее.

Рис. 2.6. Классификация погрешностей средств измерений

 

По закономерности проявления при повторных измерениях одной и той же физической величины принято выделять систематическую D_с и случайную 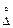погрешности (или составляющие погрешности) средств измерений. В эти понятия в основном вкладывается тот же смысл, что и в понятия систематической и случайной погрешностей измерений (п. 1.3). Особенность здесь состоит в том, что всякое средство измерения предназначено для внесения определенности в исследуемый процесс, а наличие случайной составляющей погрешности приводит к неоднозначности. В связи этим первая задача, которую обычно решают при создании средств измерений, состоит в том, чтобы случайную погрешность сделать незначительной. Если это условие выполняется, а элементы, входящие в состав средства измерения, стабильны, можно путем градуировки обеспечить достаточно малые систематические погрешности средства измерения.

В зависимости от условий применения измерительных устройств различают основную и дополнительную погрешности.

Основной погрешностьюD_о средства измеренийназывают погрешность при использовании его в нормальных условиях. Нормальными являются условия, которые характеризуются значениями влияющих величин, при которых изменением результата измерений пренебрегают вследствие малости.

Нормальные условия измерений устанавливают в нормативных документах на средства измерений конкретного типа. В большинстве случаев к нормальным относят следующие внешние условия:

температура окружающей среды 293 К ± 5 К;

относительная влажность воздуха 65 % ± 15 %;

атмосферное давление 103,3 кПа ± 4 кПа (750 мм рт. ст. ± 30 мм рт. ст.);

напряжение питающей электрической сети 220 В ± 2 % с частотой 50 Гц.

Не все эти признаки нормальных условий обязательны для средств измерений. Только нормальная температура окружающей среды (с некоторым допустимым отклонением) является почти всегда обязательной. При использовании средств измерений в нормальных условиях считают, что влияющие на них величины практически никак не изменяют их характеристики.

При выходе условий измерения за границы нормальных условий возникают дополнительные погрешности. Дополнительная погрешность D_д средства измерения – это погрешность, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального значения или вследствие ее выхода за пределы нормальной области значений.

Зачастую поэтому для средств измерений устанавливают рабочие условия измерений. Рабочими называют условия измерений, при которых значения влияющих величин находятся в пределах рабочих областей, и в этих пределах нормируют дополнительную погрешность D_д. Рабочие условия обычно таковы, что изменения значений влияющих величин для них существенно больше, чем для нормальных условий, т.е. область рабочих условий включает в себя область нормальных условий. Например, рабочие температуры многих типов средств измерений имеют пределы -10 °С…+40 °С.

Изменение погрешности, как и других характеристик средств измерений под действием влияющих величин, описывают функциями влияния. Функция влияния – это зависимость изменения какой-либо метрологической характеристики средства измерения от изменений влияющей величины или совокупности влияющих величин в рабочих условиях его применения.

В зависимости от характера изменения величины в процессе измерения погрешности средств измерений разделяют на статические и динамические.

Статической D_stназывают погрешность средства измерений в случае измерения величины, принимаемой за неизменную. Динамическая погрешность D_dyn возникает при измерении изменяющейся (в процессе измерений) величины.

 

По форме представления погрешности делят на абсолютные, относительные и приведенные. Понятия абсолютной D и относительной d погрешностей средств измерений близки рассмотренным ранее погрешностям измерений (п. 1.3, формулы 1.6 и 1.9). Приведенная погрешность g средства измерения представляет собой отношение абсолютной погрешности D средства измерения к нормирующему значению Х_N. Нормирующее значение – это условно принятое значение величины, постоянное во всем диапазоне измерений или в части диапазона. Приведенная погрешность g вычисляется по формуле

. (2.15)

Часто за Х_N принимают верхний предел измерений или диапазон измерений средства измерений. Выражают приведенную погрешность обычно в процентах.

 

Чрезвычайно важным для применения средств измерений и правильной оценки погрешности измерений, получаемой при их использовании, являются сведения о зависимости погрешности от значения измеряемой величины в пределах диапазона измерений, а также сведения об изменениях этой погрешности под действием влияющих величин.

Зависимость погрешности от значения измеряемой величины определяется принятой конструкцией (схемой) и технологией изготовления средства измерения. Из-за несовершенства конструкции и технологии изготовления реальная функция преобразования Y=f_p(X) средства измерения отличается от номинальной Y=f_н(X). Отклонения реальной функции преобразованияот номинальной зависят от значения измеряемой величины. По этому признаку погрешности принято разделять на аддитивную, мультипликативную, линейности и гистерезиса (рис. 2.7).

 

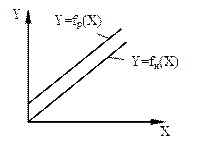
а)	б)
в)	г)
д)	е)

 

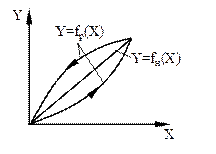
Рис. 2.7. Реальная и номинальная функции преобразования: а, б – аддитивная погрешность, в, г – мультипликативная погрешность, д – погрешность линейности, е – погрешность гистерезиса

 

Аддитивная (получаемая путем сложения) – это погрешность, которая остается постоянной при всех значениях измеряемой величины. Аддитивные погрешности выражают внутренние свойства средства измерений, присущие ему независимо от внешних воздействий. Примерами такого рода служит погрешность, вызванная сдвигом шкалы прибора и погрешность, обусловленная ненулевым порогом реагирования («погрешность нуля»).

На рис. 2.7, а показано смещение реальной функции преобразования Y = f_p(X) относительно номинальной Y = f_н(X), при этом выходной сигнал средства измерения при всех значениях измеряемой величины Х будет больше или меньше на одну и ту же величину, чем он должен быть, в соответствии с номинальной функцией преобразования.

Если аддитивная погрешность является систематической, то она может быть устранена. Для этого в средствах измерений обычно имеется специальный настроечный узел (корректор) нулевого значения выходного сигнала. Если аддитивная погрешность является случайной, то ее нельзя исключить полностью, а реальная функция преобразования смещается по отношению к номинальной во времени произвольным образом. При этом для реальной функции преобразования можно определить некоторую полосу (рис. 2.7, б),ширина которой остается постоянной при всех значениях измеряемой величины.

Возникновение случайной аддитивной погрешности обычно вызвано трением в опорах, контактными сопротивлениями, дрейфом нуля, шумом и фоном средства измерения.

Мультипликативная (получаемая путем умножения) – это погрешность, которая линейно возрастает (или убывает) с увеличением измеряемой величины. Примером такой погрешности является погрешность измерительного преобразователя, обусловленная отличием действительного коэффициента преобразования от номинального. Графически появление мультипликативной погрешности интерпретируется поворотом реальной функции преобразования относительно номинальной (рис. 2.7, в). Если мультипликативная погрешность является случайной, то реальная функция преобразования представляется полосой, показанной на рис. 2.7, г. Причиной возникновения мультипликативной погрешности обычно является изменение коэффициентов преобразования отдельных элементов и узлов средств измерений.

На рис. 2.7, д показано взаимное расположение номинальной и реальной функций преобразования средства измерения в случае, когда отличие этих функций вызвано нелинейными эффектами. Если номинальная функция линейная, то вызванную таким расположением реальной функции преобразования систематическую погрешность называют погрешностью линейности. Ее причинами могут быть конструкция средства измерения и нелинейные искажения функции преобразования, связанные с несовершенством технологии производства.

Наиболее существенной и трудно устраняемой систематической погрешностью измерительных устройств является погрешность гистерезиса, выражающаяся в несовпадении реальной функции преобразования при увеличении (прямой ход) и уменьшении (обратный ход) измеряемой величины (рис. 2.7, е ).

Погрешность гистерезиса приводит к вариации выходного сигнала. Вариация представляет собой разность показаний, получаемых при измерениях одного и того же значения измеряемой величины, сначала – приближением к нему со стороны меньших значений (прямой ход), затем – со стороны больших значений шкалы (обратный ход).

Причинами гистерезиса являются люфт и сухое трение в механических передающих элементах, гистерезисный эффект в ферромагнитных материалах, внутреннее трение в материалах пружин, явление упругого последействия в упругих чувствительных элементах, явление поляризации в электрических, пьезоэлектрических и электрохимических элементах и др.