Конструктивный расчет колонны.

6.1. Конструирование и расчет стержня колонны.

а) Исходные данные: Требуется подобрать сечение сплошной верхней и сквозной нижней частей колонны.

Расчетные усилия согласно таблице 5.2 и пояснениям к ней:

- для верхней части колонны (в узле «В»):

М= - 253 кН·м; N= - 367 кН;

- для нижней части колонны:

М₁=-303 кН·м; N= - 954 кН – момент догружает подкрановую ветвь;

М=548 кН·м; N= - 1029 кН – момент догружает шатровую ветвь.

Максимальное значение поперечной силы Q_max=84кН.

Соотношение жесткостей верхней и нижней частей колонны У₁/У₂=0,14.

Материал колонны: сталь С235 по ГОСТ 27772-88, R_y=230МПа при t=2…20мм и для листа и для фасона.

б) Расчетные длины колонны.

Расчетные длины колонны определяем в соответствии с приложением 6[2] учитывая, что в нашем случае верхний конец колонны закреплен только от поворота. При этом, поскольку

, используя данные таблицы 18[2] получим, что

μ₁=2; μ₂=3.

Таким образом, расчетные длины в плоскости рамы будут:

- для нижней части колонны

- для верхней части колонны

Расчетные длины из плоскости рамы нижней и верхней частей колонны соответственно равны:

где: h_cb=1,5м – высота подкрановой балки.

в) Подбор сечения верхней части колонны.

Сечение верхней части колонны принимаем в виде сварного двутавра с высотой сечения h₂=450мм.

Требуемая площадь сечения определяем, используя формулу Ф.С.Ясинского:

Полагая - среднее значение, получим:

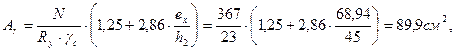
где: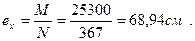

Компонуем сечение с учетом ограничений условиями местной устойчивости.

Поскольку относительный эксцентриситет

где: ρ=0,35·h₂=0,35·45=15,75см – ядровое расстояние, и

то по табл.27^*[2]

На этапе компоновки используем условие предельного отношения расчетной высоты стенки к ее толщине согласно п.7.14^*[2] в форме:

Правая часть условия:

Тогда принимаем толщину полок t_f=10мм, будем иметь высоту стенки

h_w=h₂-2t_f=45-2·1,0=43см. Толщина стенки определяется из вышеприведенного условия:

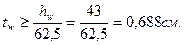
Принимаем: t_w=7мм.

На один пояс будет приходиться:

При t_f=10мм, ширина полки составит:

что больше минимально необходимой ширины полки из условия устойчивости колонны из плоскости момента.

Предельное же согласно табл. 29^*[2] отношение ширины полки к ее толщине:

Принимаем: h₂=45см; h_w=43см; t_w=0,7 см; b_f=30см; t_f=1,0см.

При этом фактическая площадь сечения верхней части сечения колонны составит:

А=2·30·1+43·0,7=90,1 см².

Геометрические характеристики сечения:

I_x = + 2×30×1,0×[(45 - 1,0)/2]² =33677 см⁴;

I_y = =4500 см⁴;

m_x = = =4,14;

= = 1.

По таблице 73[2] коэффициент формы сечения:

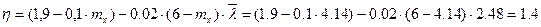
Приведенный относительный эксцентриситет:

m_ef = η×m_x = 1,4×4,14=5,8.

По таблице 74[2] φ_е = 0,1782;

Проверка устойчивости верхней части колонны в плоскости действия момента примет вид:

σ_x = =21,72 кН/см² < R_y = 23 кН/см².

Недонапряжение составляет:

,

Проверка устойчивости верхней части колонны из плоскости действия момента:

. По табл.72[2]: φ_y = 0,872

Для определения m_x найдём максимальный момент в пределах средней трети расчётной длины верхнего участка колонны (рис. 6.2).

= = - 266 кН×м;

Рисунок 6.2.

При этом М_x,1/3=-266кН·м > M_max/2=-346/2=-173 кН·м.

Поэтому согласно п.5.31[2]: где по табл.10 [2]:

поэтому β=1. При полученных данных:

с=1/(1+0,868·4,36)=0,209.

Тогда:

Проверим местную устойчивость стенки согласно п.7.16^*[2].

Наибольшее сжимающее напряжение у расчетной границы стенки:

Соответствующее напряжение у противоположной кромки

Значение (σ принимается со знаком «+» - п.7.16[2]).

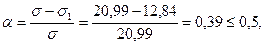
в связи с чем, проверку местной устойчивости стенки выполняем в соответствии с п.7.14^*[2]. Согласно указанному пункту, отношение расчетной высоты стенки к ее толщине должно подчиняться условию:

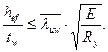(а)

В нашем случае (рис.6.1):

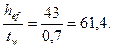
В соответствии с таблицей 27^*[2], при значении относительного эксцентриситета m>1 для двутаврового сечения при условной гибкости элемента в плоскости действия момента

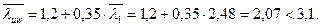
Тогда правая часть неравенства (а) будет равна:

Таким образом, выше приведенное условие (а) примет вид:61,4<61,9. Следовательно, местная устойчивость стенки обеспечена. Сечение верхней части колонны показано на рис.6.1

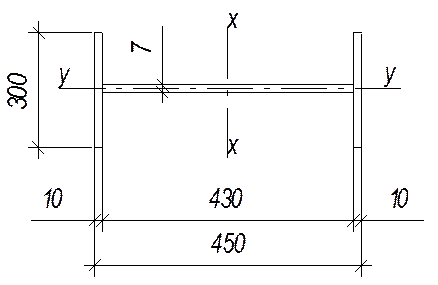
Рисунок 6.1 Поперечное сечение надкрановой части колонны.

г) Подбор сечения нижней части колонны.

Нижнюю часть колонны проектируем сквозного сечения, состоящую из двух ветвей, соединенных решеткой. Высота сечения h₁=1000мм.

Подкрановую (внутреннюю) ветвь колонны принимаем из широкополочного двутавра, шатровую (наружную) – составного сварного сечения из трех листов.

Действующие на ветви колонны усилия составляют (комбинация усилий для ветвей):

- для расчета подкрановой ветви

М= - 303кН·м; N= - 954кН;

- для расчета шатровой ветви

М=+548 кН·м; N= - 1029кН;

Расчетная длина нижней части колонны в плоскости действия моментов l_efx1=21,22м, из плоскости действия моментов l_efy1=10,61м.

Ветви между собой соединяются решеткой из одиночных уголков, располагаемых под углом 40-45⁰ к горизонтали (раскосами) в сочетании со стойками.

Поскольку проектируемое сечение является несимметричным, то задаемся:

у₂= 0,4· h₁= 0.4·1.0=0.4 м.,

у₁= h₁-у₂=1-0,4=0,6 м.

Здесь: у₂- расстояние от центра тяжести всего сечения до наиболее нагруженной (шатровой) ветви.

Максимальные усилия:

- в шатровой ветви:

кН;

- в подкрановой ветви:

кН.

Расчет подкрановой ветви

Из условия обеспечения общей устойчивости колонны из плоскости действия момента (из плоскости рамы), высоту двутавра подкрановой ветви назначаем в пределах 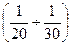Н₁, что соответствует гибкости λ=60…100.

При Н₁=10,61 м, высота двутавра должна быть в пределах

от 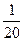10,61 = 53,05см до = 35,37 см.

Назначаем двутавр № 35Б1 по ГОСТ 26020-83 (см. приложение 5) со следующими геометрическими характеристиками:

h=346 мм.; А_в1=49,53 см²; Ĵ_x=10060 см⁴;

W_x=581,7 см³ ; i_x=14,25 см; J_y=529,6 см⁴;

i_y=3,27 см; t_f=8,5 мм; t_w=6,2 мм; b_f=155 мм.

Гибкость , чему соответствует φ=0,732.

Проверка устойчивости ветви (сталь С235 по ГОСТ 27772-88, R_y=230 МПа при t=2…20 мм).

кН/см² < Ry·γc = 23·0,95=21,85 кН/см²

Гибкость ветви в плоскости действия момента при расстоянии между узлами решетки l_в=1000 мм (по оси у₁-у₁ рис. 6.3):

<λ_u,

т.е. условие выполняется.

Расчет шатровой ветви

Ориентировочная площадь сечения ветви при средних значениях φ=0,75:

см^2.

Для удобства прикрепления элементов решетки , просвет между внутренними гранями полок принимаем равным расстоянию между внутренними гранями полок двутавра подкрановой ветви, т.е. 329 мм. Толщину стенки швеллера для удобства ее соединения встык с полкой надкрановой части колонны принимаем равной t_w2=10 мм. Высота стенки швеллера из удобства размещения сварных швов будет b_f2=395мм (с учетом размеров проката).

Тогда требуемая площадь полок будет:

см².

Из условия местной устойчивости полки швеллера:

Поэтому принимаем: b_f=200мм; t_f=10 мм; А_f=20см².

Геометрические характеристики ветви:

А_в2=39,5·1,0+2·20=79,5 см²;

Z₀=(1,0·39,5·0.5+20·11·2)/85=5,4 см;

J_y2=1,0·45·4,9 ²+2·1,0·20³/12+2·1,0·20·5.6²=3668,2 см;

см⁴;

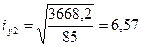см; см.

Уточняем положение центра тяжести всего сечения колонны (см. рис. 6.3):

Рисунок 6.3 Поперечное сечение подкрановой части колонны.

h₀=h₁-z₀=1000-54=946 мм;

у₁=А_в2·h₀/(А_в1+А_в2)=85·94,6/(122,4+85)=38,8 см;

у₂=94,6-38,8=55,8 см.

В связи с незначительным отличием у₁ и у₂ от первоначально принятых размеров, усилия в ветвях не пересчитываем.

Проверяем устойчивость шатровой ветви:

; φ_у=0,789;

кН/см² <R_y·γ_c=21.85 кН/см²

Гибкость шатровой ветви в плоскости действия момента при расстоянии между узлами решетки l_в2=1000 мм:

; φ=0,975.

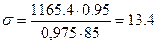кН/см² <R_y·γ_c=21,85 кН/см² .

Расчет решетки подкрановой части колонны

В соответствии с таблицей 5.2 максимальное значение поперечной силы в колонне Q_max=84 кН., что больше значения фиктивной поперечной силы

Q_fic≈0.2·(А_в1+А_в2)=0,2·(122,4+85)=41,48 кН

В связи с этим решетку рассчитываем на большую поперечную силу Q=84 кН.

Усилие сжатия в раскосе:

кН,

; α=45⁰; sinα =0.707

Задаемся гибкостью раскоса λ_d=100. Тогда в соответствии с таблицей 72 [2]

φ =0,556.

Требуемая площадь сечения раскоса:

см²,

где γ_с=0,75 – принят в соответствии с табл. 6 [2] как для сжатого элемента решетки пространственной конструкции, прикрепляемого к поясам одной полкой.

В соответствии с ГОСТ 8509-93 «Равнополочные уголки» (см. приложение 5) принимаем сечение раскоса из одиночного уголка 70х5 со следующими геометрическими характеристиками А_d=6,86 см²; i_x=2,16 см; i_min =1,39 см.

Длина раскоса м, . Тогда φ=0,546

Напряжения в раскосе:

кН/см² <R_y·γ_c=23·0.75=17.25 кН/см².

Недонапряжение в раскосе 12,3 %. Гибкость раскоса не превышает предельную, ограничиваемую нормами [2].

Проверка устойчивости колонны в плоскости действия момента как единого целого стержня

Геометрические характеристики всего сечения:

А=А_в1+А_в2=122,4+85=207,4 см³;

J_x=A_в1·у₁²+А_в2·у₂²=122,4·38,8²+85·55,8 ²=448925 см⁴;

см;

Приведенная гибкость:

,

где , h₀-см. рис. 6.3;

l₁=lв=1000 мм; .

Для комбинаций усилий, догружающих шатровую ветвь:

М=548 кНм, N=1029 кН,

.

По табл. 75 [2] φ_е=0,399.

Тогда

кН/см² < 21,85 кН/см²= R_y·γ_c.

Для комбинаций усилий,догружающих подкрановую ветвь:

М₁=303 кНм; N₁=954 кН,

; φ_е=0,56.

кН/см² < 21,85 кН/см²= R_y·γ_c.

Устойчивость сквозной колонны как единого стержня из плоскости действия момента проверять не надо, т.к. она обеспечена проверкой устойчивости отдельных ветвей.

6.2 Конструирование и расчет узла сопряжения верхней и нижней части колонны

Расчетные комбинации усилий в сечении над уступом (см. таблицу 5.2):

а) М=+345 кНм; N=-496 кН;

б) М=-169 кНм; N=-866 кН.

Давление кранов D_max=2037 кН.

Прочность стыкового шва (ш.1 по рис. 6.4) проверяем по нормальным напряжениям в крайних точках сечения надкрановой части. Площадь шва равна площади сечения колонны. Принимаем полуавтоматическую сварку сварочной проволокой Св-08Г2С по ГОСТ 2246-70^* в углекислом газе по ГОСТ 8050-85. Расчетное сопротивление сварного соединения R_wy=R_y=230МПа (23 кН/см²);

Коэффициент условия работы шва γ_c=0,95

Первая комбинация М и N:

- наружная полка:

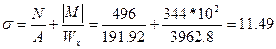кН/см²<21,85 кН/см² ,

где:

R_wy* γ_c=23*095=21,85 кН/см²

- внутренняя полка

кН/см²<21,85 кН/см²

Вторая комбинация М и N:

- наружная полка:

кН/см²<21,85 кН/см² ,

- внутренняя полка:

кН/см²<21,85 кН/см² .

Толщину стенки траверсы определяем из условия ее смятия.

Расчетное сопротивление смятию торцевой поверхности (имея в виду наличие пригонки):

кН/см²,

где:

R_un=36 кН/см² - нормативное значение временного сопротивления для листовой стали С235 по ГОСТ 27772-88 при t=2÷20 мм и t от 20 до 40 мм [2];

γ_m=1,025 – коэффициент надежности по материалу.

Тогда:

см,

где l_ef=b_s+2t_pl=40+2*2=44 см, (b_s-ширина опорного ребра подкрановой балки – см.рис.6.4).

Принимаем t_tr=14 мм.

Усилие во внутренней полке верхней части колонны (вторая комбинация М и N):

кН.

Определяем длину шва крепления внутренней полки верхней части колонны к стенке траверсы (ш.2 по рис. 6.4). Примем полуавтоматическую сварку проволокой марки Св-08А по ГОСТ 2246-70^*, d=(1,4÷2)мм, к_fmin=6 мм (табл.38^*[2]), β_f=0,9; β_z=1,05 (табл.34^*[2]); R_wf=180 МПа,

R_wz=0,45*R_un=0,45*360=162 МПа. При этом условие (п.11.2^*[2])

R_wz<R_wf≤R_wz* ; см,

162<180<189 выполняется и, следовательно, расчет можно вести только по металлу шва:

см,

19,8 см <85*β_f*k_f=85*0,9*0,6=45,9 см.

В стенке подкрановой ветви делаем прорезь, в которую заводим стенку траверсы.

Для расчета шва крепления траверсы к подкрановой ветви (ш.3 по рис.6.4) составляем комбинацию усилий, дающую наибольшую опорную реакцию траверсы. Такой комбинацией будет сочетание (см. табл.5.1) 1,2,6,5(-),7:

кН.

Здесь 0,9 учитывает, что N и М взяты со второго основного сочетания нагрузок.

Требуемая длина шва:

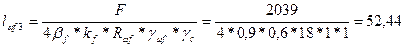см>

>85 см

Увеличиваем катет шва, приняв его k_f=7мм.

Тогда см<85*0,9*0,7=53,5 см.

Требуемую высоту траверсы h_tr определяем из условия прочности стенки подкрановой ветви (сечение 1-1 по рис. 6.4):

см,

где:tω=9.5 мм – толщина стенки двутавра №40Ш1.

Принимаем h_tr=810 мм.

Проверяем прочность траверсы как балки, нагруженной N, М и D_max. Расчетная схема и сечение траверсы приведены на рис. 6.4.Нижний пояс траверсы принимаем из листа 360х14 мм, верхние горизонтальные ребра –из двух листов 150х14 мм.

Геометрические характеристики траверсы:

-положение центра тяжести сечения:

см,

-момент инерции относительно центральной оси «х»:

;

-момент сопротивления для наиболее удаленной точки сечения от центральной оси «х».

.

Максимальный изгибающий момент в траверсе М_tr при комбинации усилий «б» (см. начало п. 6.2 и рис. 6.4):

Нормальное напряжение в траверсе:

<R_y*γ_c=23кН/см²

Максимальная поперечная сила в траверсе с учетом усилия от кранов (комбинация усилий та же, что и при расчете сварного шва ш.3):

где: k-коэффициент, учитывающий неравномерную передачу давления D_max.

Касательные напряжения:

<

<R_s*γ_c=(0.58*23)*1=13,34 кН/см².

6.3. Конструирование и расчет базы колонны

Проектируем базу раздельного типа.

Расчетные комбинации усилий в нижнем сечении колонны (см. таблицу 5.2):

а) М=+973 кНм; N=-2994 кН – для шатровой ветви;

б) М=-365 кНм; N=-2624 кН- для подкрановой ветви.

Усилия в ветвях колонны:

- в шатровой ветви:

- в подкрановой ветви:

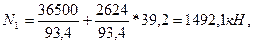
т.е. наиболее нагруженной является база шатровой ветви.

База шатровой ветви

Требуемая площадь плиты:

где: R_вр=11,5 МПа – расчетное сопротивление бетона осевому сжатию; класс бетона В20 (табл. 13 [4]).

Ширина плиты В_pl=b_f2+2c₂=40,4+2*6,3=53 см.

(с_2min=4см – минимальный размер свеса плиты).

Принимаем B_pl=53 см, тогда длина плиты

Принимаем L_pl=46 см.

Фактическая площадь плиты:

>А_pl,tr=2416,7 см²

Среднее напряжение в бетоне под плитой: .

Из условия симметричного расположения траверс относительно центра тяжести ветви, расстояние между траверсами в свету равно (см. рис.6.3.): 2*(20+1,8-6,6)=30,4 см.

Определяем толщину плиты из условия ее работы на изгиб:

- участок №1 (консольный свес с = с₁=6,6 см – рис. 6.5):