Методические рекомендации к расчетному заданию № 1

РАСЧЕТНОЕ задание № 1

«Светотехнические характеристики и их использование в телевидении»

Расчетное задание № 1

Телевизионная (ТВ) передача ведется при помощи передающей камеры с трубкой типа (определяется видом фотокатода) при освещении источником типа при коэффициенте яркости передаваемой сцены . Передающая камера имеет объектив с относительным отверстием и прозрачностью . Освещенность трубки составляет .

Требуется:

1. Рассчитать необходимую освещенность фотокатода трубки.

2. Определить необходимую освещенность объекта ТВ передачи .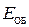

Таблица 1.1 — Исходные данные к расчетному заданию № 1

M
	0,4	0,5	0,7	0,75	0,65	0,45	0,55	0,60	0,35	0,48
О	1:2	1:3	1:1,5	1:3,5	1:1,75	1:1,6	1:2	1:1,8	1:1,9	1:2,1
N
	СЦ	ВС	СЦ	ВС	СЦ	ВС	СЦ	ВС	СЦ	ВС
	0,8	0,9	0,8	0,9	0,8	0,9	0,8	0,9	0,8	0,9
И	С	В	С	В	С	В	С	В	С	В
, лк	1,4	1,6	0,8	0,6	0,7	0,9	1,2	1,35	1,0	1,55

Методические рекомендации к расчетному заданию № 1

Источником ТВ сигнала может быть любое излучение в оптическом диапазоне, испускаемое, пропускаемое и отражаемое наблюдаемым объектом и окружающей ею средой. Для воспроизведения изображения можно использовать излучение лишь в узком диапазоне волн от 380 нм до 770 нм, воспринимаемое глазом человека в виде света. Различают монохроматические излучения (имеющие одну длину волны) и сложные излучения (характеризуются спектральным распределением энергии).

Количественная характеристика источника излучения — цветовая температура T _цта действительная температура, до которой необходимо нагреть абсолютно черное тело, чтобы получить излучение данного цвета.

Стандартизованы следующие источники: А (T _ц составляет 2854 ), (T _ц составляет 4800 ) и (T _ц составляет 6500 ).

Для оценки излучения используется система величин, основанных на спектральной чувствительности образцового приемника, а именно: система световых величин, построенная на основе спектральной чувствительности глаза стандартного наблюдателя или кривой видности глаза (см. рис. 1.1).

Система световых величин включает следующие характеристики.

1. Световой поток Ф — поток излучения, оцениваемый по зрительному ощущению, (измеряется в лм):

^,

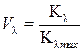где: К _l — спектральная эффективность при данной l;

К _{l max} — максимальная световая эффективность для стандартного наблюдателя (величина К _{l max} составляет 683 лм/Вт при l, равной 555 нм).

2. Сила света I характеризует пространственную плотность светового потока и определяется в канделах (кд)

^,

где: dW— телесный угол (стерадиан), в котором заключен световой поток dФ;

^,

где: r — радиус сферы.

Для равномерного светового потока

3. Яркость В характеризует светящуюся поверхность

(размерность — кд/м²) и определяется отношением силы света к площади светящейся поверхности

^,

или

то есть отношение силы света к проекции светящейся поверхности на плоскость, перпендикулярную направлению наблюдения.

Если распределение силы света поверхностного источника подчиняется закону Ламберта (закону косинуса), то есть

,

то

.

Так как наблюдаемая яркость не зависит от угла наблюдения, такие излучатели называют равнояркими.

4. Светимость М — характеризует поверхностную плотность светового потока равнояркого источника и представляет собой суммарный световой поток dФ, излучаемый светящейся поверхностью d S в пределах угла 2p (размерность — лм/м²):

5. Освещенность Е — характеризуется поверхностной плотностью светового потока dФ на облучаемой поверхности d S, то есть отношение светового потока к площади освещаемой поверхности (размерность — лк)

6. Коэффициент яркости r_В представляет собой отношение яркости В _a в заданном направлении к яркости В ₀ идеального равнояркого источника.

При использовании телевизионных устройств часто возникают проблемы, для решения которых применяются световые величины:

— необходимо определить требуемую освещенность объекта, при которой будет обеспечена качественная телевизионная передача;

— по известной освещенности объекта (или интервалу возможных значений освещенности) определить чувствительность передающей трубки ТВ камеры, и затем выбрать трубку нужного типа.

Освещенность объекта Е _ОБ и освещенность фотокатода Е _ФК передающей ТВ трубки связаны следующим образом:

.

Необходимая освещенность Е _ФК на фотокатоде трубки обычно задается в справочной литературе, однако при этом следует учитывать, что интегральная чувствительность фотокатодов e ^А определяется при их освещенности источником А, поэтому при другом источнике необходимая освещенность будет иной. Освещенность определяют, используя зависимость интегральной чувствительности фотокатода от цветовой температуры источника (см. рис.1.2).

 

Рисунок 1.1 — Кривая видности глаза

 

Рисунок 1.2 — Интегральная чувствительность фотокатода ТВ трубки:

1 — сурьмяно-цезиевый (СЦ) фотокатод; 2 — висмусто-серебрянный (ВС) фотокатод

 

РАСЧЕТНОЕ задание № 2

«КОЛОМЕТРИЧЕСКИЕ СИСТЕМЫ RGB И XYZ. ЦВЕТОВОЙ ГРАФИК И ЕГО ИСПОЛЬЗОВАНИЕ ДЛЯ ОЦЕНКИ КАЧЕСТВА ЦВЕТНЫХ ТЕЛЕВИЗИОННЫХ ИЗОБРАЖЕНИЙ»

Расчетное задание № 2

На модуляторы цветного кинескопа подаются сигналы основных цветов (красного R, зеленого G, синего В) с амплитудами E_R, E_G, E_B, соответственно.

Требуется:

1. Определить цвет, получаемый на экране цветного кинескопа при заданных значениях амплитуд сигналов основных цветов E_R, E_G, E_B.

2. Определить, как изменится цвет, воспроизводимый на экране, при увеличении амплитуды каждого из сигналов основных цветов на 0,1.

3. Определить, как изменится цвет, воспроизводимый на экране, при уменьшении амплитуды каждого из сигналов основных цветов на 0,1.

Таблица 2.1 — Исходные данные к расчетному заданию № 2

M
ER	0,25	0,45	0,55	0,85	0,7	0,6	0,4	0,25	0,3	0,2
N
EB	0,3	0,5	0,8	0,9	0,7	0,35	0,25	0,4	0,2	0,20
EG	0,2	0,3	0,5	0,7	0,3	0,4	0,6	0,2	0,8	0,9

Методические рекомендации

Основные законы смешения цветов:

— любые четыре цвета находятся в линейной зависимости, однако существует неограниченное количество комбинаций из трех цветов, являющихся линейно независимыми;

— непрерывному изменению частоты излучения соответствует непрерывное изменение цвета;

— цвет смеси зависит только от цветов смешиваемых компонентов и не зависит от способа их получения, в частности, от их спектрального состава.

Из первого закона следует, что любой цвет может быть выражен одной комбинацией из трех линейно независимых цветов, которые в данной колориметрической системе называются основными. Так как цвет является трехмерной величиной, то он может быть представлен вектором в трехмерном пространстве (цветовом пространстве).

Длина вектора характеризует количество цвета, а направление вектора его качество, то есть его цветность.

2.3. Cистема RGB

В системе RGB в качестве основных цветов стандартизированы красный R

(l=700 нм), зеленый G (l=546,1 нм) и синий В (l=435,8 нм) цвета.

Любой произвольный цвет F выражается через основные цвета R, G, B линейным уравнением:

,

где f', r', g', b' — количества (модули) соответствующих цветов, выраженные в единичных значениях;

R, G, и B — единичные векторы основных цветов;

,

или

,

где

Трехцветные коэффициенты

. (2.1)

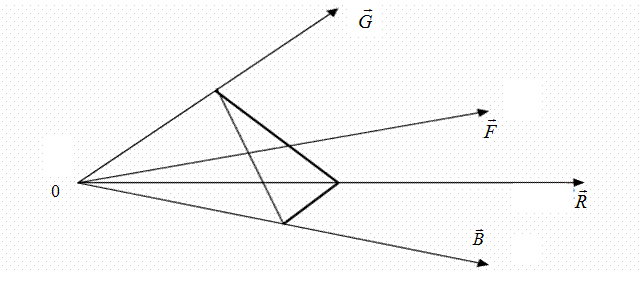
Цветность является двумерной величиной, так как из (2.1) может быть определена цветность при двух известных. Плоскость, проходящая через единичное значение векторов — единичная, и в пространстве образуется цветовой треугольник (см. рис. 2.1). Любой точке в плоскости треугольника соответствует вполне определенная цветность.

Для получения белого равноэнергетического цвета Е яркостные коэффициенты B_R', B_G', B_B' единичных количеств цветов должны удовлетворять соотношению:

B_R': B_G': B_B' = 1: 4,59: 0,06.

По причине разномасштабности основных цветов системы RGB чистые спектральные цвета не могут быть получены смешением этих естественных цветов,

 

Рисунок 2.1 — Система RGB

Рисунок 2.2 — Система XYZ

так же как и некоторые реальные цвета, координаты которых находятся вне пределов треугольника RGB. Так как коэффициенты r', g', b' при расчетах принимают отрицательные значения, что противоречит физическому пониманию цвета, была принята система XYZ.

2.4. Колометрическая система XYZ

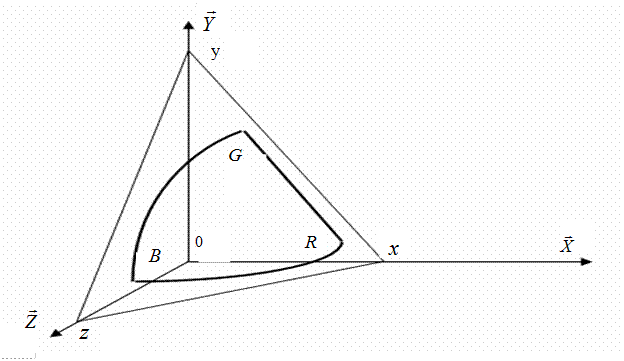
В качестве основных в системе XYZ приняты нереальные цвета, но при этом плоскость XOZ является плоскостью нулевой яркости, цветовой треугольник XYZ (см. рис. 2.2) полностью охватывает локус. То есть все реальные цвета, в том числе и спектрально чистые, характеризуются положительными значениями координат в этой системе.

Для равноэнергетического белого цвета

Связь систем XYZ и RGB выражается соотношением

.

Для системы XYZ справедливо

Fx: Fy: Fz = 0:1:0,

то есть яркостный коэффициент любого цвета в плоскости XYZ однозначно определяется координатой y.

Однако для расчетов пользуются не плоскостью единичных цветов, а ее проекцией на плоскость XOY, которую называют диаграммой цветности (см. рис. 2.3). При этом точка Z совмещается с точкой 0 и, соответственно, ось OX на диаграмме цветности является бесцветной (алихной), а прямые y =const — линиями с постоянными значениями яркостных коэффициентов.

При известных значениях модулей x', y', z' координаты цветности находят из следующих выражений:

 

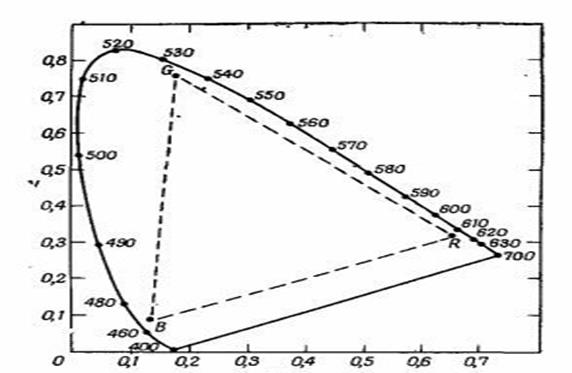
Рисунок 2.3 — Диаграмма цветности

Свойства и правила пользования диаграммой цветности:

— реальные цвета лежат внутри локуса и определяются положительными координатами x, y.

— цветность равноэнергетического белого цвета Е: x_E = 1/3; y_E = 1/3.

— цвет смеси двух реальных цветов лежит на прямой, соединяющей смешиваемые цвета.

— дополнительный цвет лежит на пересечении с локусом прямой, проходящей через точку Е и точку с координатами (на локусе) цвета.

— цвет смеси любых трех реальных цветов лежит внутри треугольника, в вершинах которого находятся эти реальные цвета.

Основные цвета системы RGB в системе XYZ имеют следующие координаты:

2.5. Оценка цветовых искажений воспроизводимых телевизионных изображений

На модулятор электронной пушки цветного кинескопа подается (для каждого цвета) сигнал с амплитудой Е.

Получаемые при этом яркости свечения люминофоров B_i должны (исходя из спектральной чувствительности глаза) находится в следующем соотношении:

B_R: B_G: B_B = 0,30 E_R:0,59 E_G:0,11 E_B,

или

B_R: B_G: B_B = m_Ry_R:m_Gy_G:m_By_{B .}

где m_R, m_G, m_B — цветовые модули основных цветов.

Координаты смеси двух цветов (и, соответственно, цвет по локусу) находят по правилу центра тяжести невесомости стержня, на концах которого расположены массы, соответствующие цветовым модулям.

Пусть F ₁(x ₁, y ₁), F₂ (x ₂, y ₂) — смешиваемые цвета, а F ₄(x ₄, y ₄) — смесь этих цветов, тогда координаты смеси:

Координаты смеси с третьим цветом F₃ (x_3, y₃) определяются из соотношений:

.

Если использовать смесь трех основных цветов кинескопа, то координаты любого цвета F находят из следующих соотношений: