Произвольный выпуклый многоугольник

Расстояние между точками

 

Проценты

Процентом называется сотая часть от числа. 1%A = 0,01A

Основные типы задач на проценты:

Сколько процентов составляет число A от числа B?

B - 100%

A - x%

Сложные проценты.

Число A увеличилось на 20%, а затем полученное число уменьшили на 25%.

Как, в итоге, изменилось исходное число?

1) A₁ = (100% + 20%)A = 120%A = 1,2A

2) A₂ = (100% - 25%)A₁=75%A₁ = 0,75A₁ = 0,75×1,2A = 0,9A = 90%A

A₁ – A = 90%A – 100%A = -10%A

3)

Þ Ответ: уменьшилось на 10%.

Изменение величины.

Как изменится время, если скорость движения увеличится на 25%?

Þ Ответ: уменьшится на 20%

 

Прямоугольный треугольник

Равнобедренный треугольник

треугольник, у которого две стороны равны.

v Углы, при основании треугольника, равны

v Высота, проведенная из вершины, является биссектрисой и медианой.

Равносильные уравнения

Равносторонний треугольник

треугольник, у которого все стороны равны.

-Все углы равны 60⁰.

-Каждая из высот является одновременно биссектрисой и медианой.

-Центры описанной и вписанной окружностей совпадают.

-Радиусы окружностей:

 

-Площадь

 

Ромб

Параллелограмм, все стороны которого равны называется ромбом.

ü Диагональ ромба является его осью симметрии. Диагонали взаимно перпендикулярны. Диагонали являются биссектрисами углов.

Скалярное произведение векторов

 

Среднее арифметическое, геометрическое

Среднее арифметическое:

Среднее геометрическое:

 

Средняя линия

Средняя линия – отрезок, соединяющий середины двух сторон треугольника.

· Средняя линия параллельна третьей стороне и равна её половине:

· Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.

Степень

 

Таблица значений тригонометрических функций

 

 

Теорема Виета

 

Приведенное квадратное уравнение: x² + px + q = 0

x₁ + x₂ = - p

x₁ × x₂ = q

 

Теорема косинусов, синусов

 

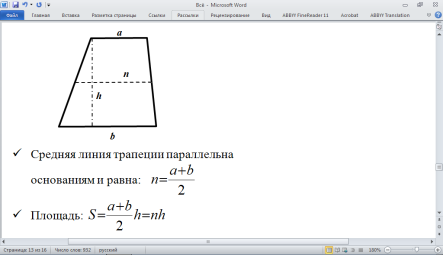
Трапеция

Четырёхугольник, у которого две стороны

параллельны, а другие не параллельны,

называется трапецией.

Углы на плоскости

 

 

Формулы сокращенного умножения

Квадрат суммы	(a + b)2 = a2 + 2ab + b2
Квадрат разности	(a - b)2 = a2 - 2ab + b2
Разность квадратов	a2 – b2 = (a + b)(a – b)

 

Куб суммы	(a + b)3 = a3 + 3a2b + 3ab2 + b3
Куб разности	(a - b)3 = a3 - 3a2b + 3ab2 - b3
Сумма кубов	a3 + b3 = (a + b)(a2 - ab + b2)
Разность кубов	a3 – b3 = (a – b)(a2 + ab + b2)

 

Функция корень

Функция модуль

 

 

Хорда

Хорда – отрезок, соединяющий две точки окружности.

-Диаметр, делящий хорду пополам, перпендикулярен хорде.

-В окружности равные хорды равноудалены от центра окружности.

-Отрезки пересекающихся хорд связаны равенством:

 

 

Центральный, вписанный угол