Основные элементы рессорного подвешивания — рессоры и пружины — характеризуются жесткостью или обратной ей величиной — гибкостью, а рессоры, кроме того, — трением. В качестве элемента рессорного подвешивания большое распространение получила резина, характеризующаяся не только гибкостью, но и способностью поглощать энергию, вызывающую колебания. Применяемые для рессорного подвешивания пневморессоры обладают свойством менять свою жесткость в зависимости от давления, содержащегося в баллонах газа.
Правильный выбор параметров этих элементов на основании детального изучения динамических характеристик подвижного состава позволяет получить высокие ходовые качества и обеспечить безопасность движения во всем диапазоне скоростей. Для рессорного подвешивания в вагонах и локомотивах применяют пружины цилиндрической формы из прутков круглого или реже прямоугольного сечения из стали ГОСТ В—2052—53* в соответствии с техническими условиями по ГОСТ 1425—62*. Для образования опорных поверхностей пружин верхний и нижний крайние витки вытягивают так, чтобы их опорные поверхности были плоскими и перпендикулярными оси пружины (рис. 1.1). Длину оттянутого конца делают равной и длины окружности. Таким образом, если пружина имеет всего п витков, то число рабочих витков, определяющих жесткость пружины,
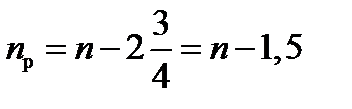
Пружину характеризуют диаметром навивки (средний диаметр витка D),числом витков, высотой в свободном состоянии Нсв и при наибольшем сжатии (до соприкасания витков) — Нс.
Для определения деформации пружины примем, что точка О (рис. 1.2) приложения силы Р все время остается на оси цилиндра и витки при действии этой силы испытывают скручивание парой сил, момент которой равен Мкр = Рг, где г — радиус витка.
Небольшим наклоном винтовой линии пренебрегаем. Для бесконечно малой части витка длиной ds, соответствующей центральному углу dβ, имеем
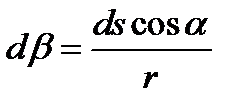
где а— угол наклона витка. Полагая cosа= 1, получим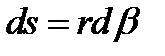 
Если принять бесконечно малую часть витка ds за прямой брус, то угол скручивания на единицу длины от крутящего момента Мкр = Рr (в случае круглого сечения)
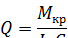
Где G—модуль упругости при кручении (G= 8000-Т-8500 кгс/мм2 или (80-85 ГПа);
Id— момент инерции
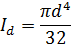
Тогда:
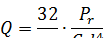
и для прямоугольного сечения прутка со сторонами b и h:
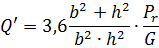
Скручивание элемента ds на угол Qds соответствует перемещению точки О приложения силы Р, равному rQds. Полное перемещение точки O (деформация пружины) при числе витков z:
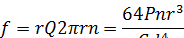
для прямоугольного сечения
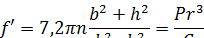
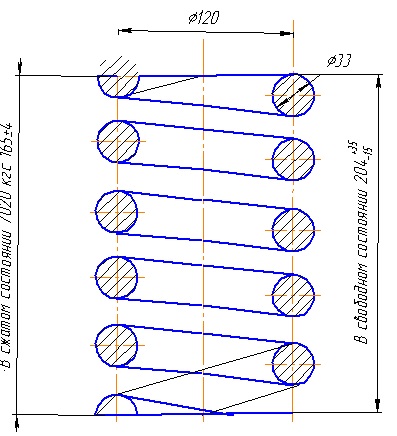
Рисунок 1.1
Для круглого сечения
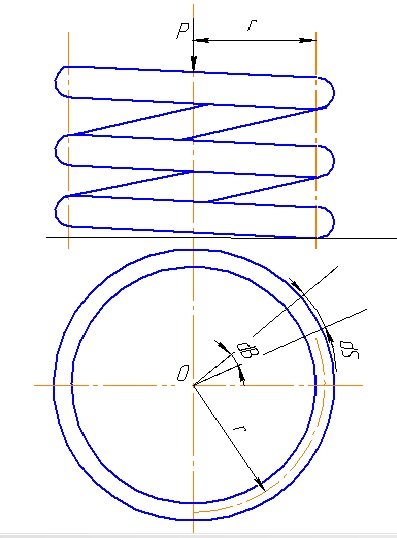
Рисунок 1.2
Жесткость пружины для круглого сечения:
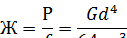
2.Эквивалентная жесткость систем
2.1. Параллельная работа системы упругих элементов
Р асчетная схема параллельной работы системы упругих элементов представлена на рис. 2.1.
Рисунок 2.1
П ри параллельной работе упругих элементов их прогибы одинаковы и равны прогибу эквивалентной рессоры f э. Нагрузка эквивалентной рессоры является суммой нагрузок отдельных упругих элементов, то есть
S = S 1 + S 2 + S 3 + … + Sn;
Жэ f э =Ж1 f э +Ж2 f э + … +Ж n 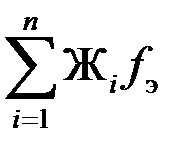f э = 
= f э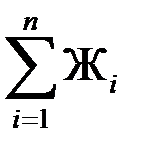 
.
Т ак как прогибы всех упругих элементов одинаковы и равны прогибу эквивалентной рессоры, в результате получаем, что
Жэ =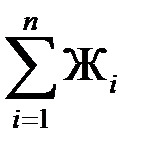 
.
Таким образом, жесткость эквивалентной рессоры системы параллельно работающих упругих элементов равна сумме их жесткостей.
2.2. Центр упругости рессорного подвешивания. Координата центра упругости
В рессорном подвешивании отмечают еще одну конструктивно не оформленную, невидимую, но работающую точку, которую называют центром упругости.
Ц ентр упругости – точка, лежащая в плоскости рессорного подвешивания, через которую проходит равнодействующая всех реакций упругих элементов рассматриваемой системы.
О тличие от эквивалентной точки подвешивания состоит в том, что через эквивалентную точку проходит тоже равнодействующая реакций упругих элементов, но только сбалансированных между собой.
Н айдем координату х 0центра упругости. Для этого рассмотрим некоторую систему упругих элементов, представленную на рис. 2.2.
Рисунок 2.2
На рис. 2.2:
Ж1, Ж2,…, Ж n – жесткости всех входящих в рассматриваемую систему упругих элементов;
f – деформация (прогиб) этих элементов;
Si – реакция i -го упругого элемента, вызванная его деформацией (прогибом);
S = S 1 + S 2 + … + Sn =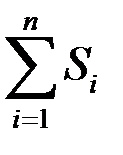 
,
где S – суммарная (равнодействующая) реакция всех упругих элементов;
О – центр упругости;
xi – расстояние i - го упругого комплекта от произвольной точки А, принятой за начало отсчета;
x 0 – расстояние от точки А до центра упругости О (координата центра упругости).
С оставляем уравнения равновесия системы действующих в ней сил:
S =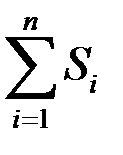 
= S 1 + S 2 + … + Sn,
где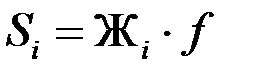 
; 
;
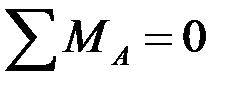S · x 0 = S 1 · x 1 + S 2 · x 2 + … + Sn · xn
или
f · x 0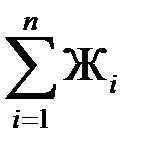 
= f · Ж1 · x 1 + f · Ж2 · x 2 + … + f· Ж n · xn = f · 
.
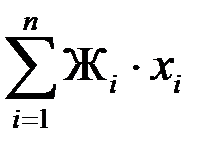О тсюда находим координату центра упругости:
x 0 =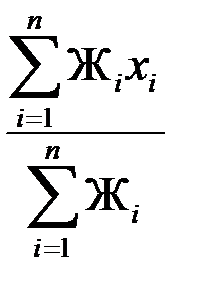 
.
2.3. Последовательная работа системы упругих элементов
Р асчетная схема последовательной работы системы упругих элементов представлена на рис. 2.3, а.
Рисунок 2.3
Н а рис. 2.3, б представлена эквивалентная схема.
В рассматриваемом случае нагрузка каждого упругого элемента S одинакова и равна нагрузке эквивалентной рессоры. Собственным весом каждого отдельного упругого элемента пренебрегаем. Следовательно,
f э = f 1 + f 2 + f 3 +…+ fn =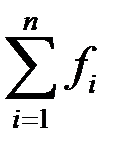 
,
причем прогиб отдельного упругого элемента fi =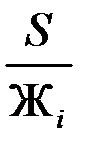 
,
а прогиб эквивалентной рессоры f э=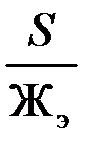 
.
Т огда
.
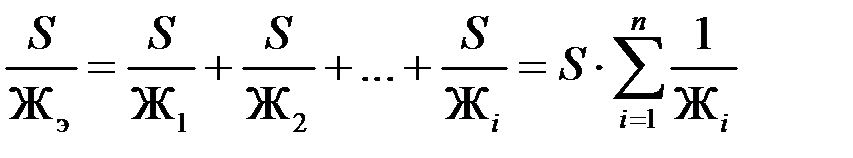В итоге
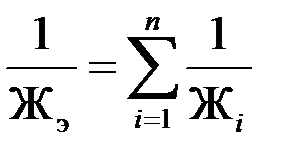
или
гэ =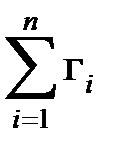 
.
Т аким образом, при последовательной работе системы упругих элементов складываются обратные их жесткостям величины, называемые гибкостями. И так, здесь прогиб эквивалентной рессоры равен сумме прогибов упругих элементов, работающих последовательно.
П рогиб i -го упругого элемента равен fi =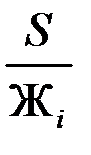 
.
Программа работы
3.1. Получить у преподавателя необходимое оборудование и исследуемые пружины.
3.2. Выполнить замеры геометрических параметров пружин, рисунок 3.1. Внести полученные значения в опытную таблицу 1
Рисунок 3.1
Таблица 1 – Геометрические параметры исследуемых пружин
| № пружины | Dвнеш, мм | d, мм | nвит, шт | nн, шт |
| … | ||||
| … |
3.3. Произвести опыт определения жёсткости пружин, рисунок 3.2. Результаты внести в опытную таблицу 2.
Рисунок 3.2
Таблица 2 – Опытная таблица для определения жёсткости пружин
| № пружины | Мгр, кг | Lпр, мм |
| 5,5 | ||
| … | ||
| 5,5 | ||
| … | ||
| … |
3.4. Произвести опыт определения эквивалентной жёсткости параллельно работающих пружин и координаты центра упругости (рисунок 3.3 а). Координату центра упругости определить опытным путем. Результаты внести в опытную таблицу 3.
Рисунок 3.3
Таблица 3 – Опытная таблица для определения эквивалентной жёсткости параллельно работающих пружин и координаты центра упругости
| № пружины | Хi, мм | № пружины | Хi, мм |
| № измерения | Мгр, кг | L, мм | Хгр, мм |
| 5,5 | |||
| … |
3.4. Произвести опыт определения эквивалентной жёсткости последовательно работающих пружин и координаты центра упругости (рисунок 3.3 б). Результаты внести в опытную таблицу 4.
Таблица 4 – Опытная таблица для определения эквивалентной жёсткости последовательно работающих пружин.
| № измерения | Мгр, кг | L, мм |
| 5,5 | ||
| … |
Оформление работы
