В общем случае при движении тела изменяются и величина, и направление вектора скорости. Для того, чтобы охарактеризовать насколько быстро происходят эти изменения, используют специальную величину — ускорение.
Мгновенным ускорением тела или его ускорением в данной точке траектории называется векторная величина, равная пределу, к которому стремится отношение изменения вектора скорости ко времени этого изменения, при неограниченном уменьшении интервала времени.
Размерность ускорения в СИ — м/с2.
При прямолинейном движении вектор скорости во всех точках направлен вдоль прямой, по которой движется тело. Вдоль этой же прямой направлен и вектор ускорения.
Прямолинейное движение называется равнопеременным, если за любые равные промежутки времени скорость тела изменяется на одну и ту же величину.
В этом случае отношение 
одинаково для любых интервалов времени. Поэтому величина и направление ускорения остаются неизменными: а = const.
Для прямолинейного движения вектор ускорения направлен по линии движения. Если направление ускорения совпадает с направлением вектора скорости, то величина скорости будет возрастать. В этом случае движение называют равноускоренным. Если направление ускорения противоположно направлению вектора скорости, то величина скорости будет уменьшаться. В этом случае движение называют равнозамедленным.
Запишем уравнения, описывающие изменение скорости и координаты тела при равнопеременном движении. Будем отсчитывать время от момента начала наблюдений за движением тела. В этом случае t0 = 0. Если конечный момент времени обозначить t, то Δt = t — 0 = t и по определению ускорения можно записать:
где v0 — скорость движения при t = 0; v — скорость в текущий момент времени t.
Отсюда получим зависимость скорости от времени движения:
v = v0+a·t. (3.5)
Можно показать, что при равнопеременном движении координата тела изменяется по квадратичному закону:
Часто при описании перехода тела из одной точки в другую (расстояние между ними s) удобно пользоваться уравнением, связывающим начальную и конечную скорость перехода:
v2-v20=2as. (3.7)
За исключением времени, все величины, входящие в уравнения (3.5—3.7), являются алгебраическими. Это означает, что численные значения скоростей (v, v), ускорения (а) и перемещения (s)
a = const. График — прямая, V = V0 + a-t — х = x0 + v0·t+ a·t2/2 —
параллельная оси f, линейная квадратичная функция
проходящая тем функция. График — График — участок
выше, чем больше наклонная прямая, параболы (t>0)
ускорение проходящая тем
круче,
чем больше ускорение.
Рис. 3.14. Графики зависимости кинематических величин от времени для равноускоренного движения
подставляются в уравнения со знаком «+», если соответствующий вектор направлен в сторону оси X, и со знаком «—» в противном случае. Обычно, при описании прямолинейного движения координатную ось X направляют в сторону движения. При таком выборе оси ускорение положительно для равноускоренного движения и отрицательно для равнозамедленного движения. На рис. 3.14 представлены графики зависимостей ускорения, скорости и координаты тела от времени равноускоренного движения.
Примеры равноускоренного движения
а) Гоночный автомобиль стартует с места и при постоянном ускорении развивает скорость 385 км/ч (107 м/с) на пути 0,4 км (400 м).
Применим формулу (3.7), из которой найдем ускорение при разгоне:
Это ускорение близко к максимально достижимому сухопутными колесными средствами и зависит от трения между колесами и дорогой. Попытки превысить эту максимальную величину путем использования более мощного двигателя приведут к проскальзыванию шин.
Время, затраченное на разгон, найдем из уравнения (3.5):
б) Найдем тормозной путь автомобиля, знать который важно не только для безопасности движения, но и в целях рациональной организации движения. Пусть, например, при скорости движения v0 = 100 км/ч (28 м/с) водитель принимает решение об экстренном торможении. Считается, что время реакции, затраченное на реализацию решения включить тормоз, составляет 0,3—1,0с. Положим его равным 0,50 с. В это время автомобиль будет двигаться равномерно и пройдет путь s1 = vo·t= 14м. На сухой ровной дороге ускорение торможения составляет 5—8 м/с2. Положим его равным 6,0 м/с2. Подставим это значение в формулу (3.7) со знаком «—» (так как движение замедленное) и найдем путь s2, пройденный от начала торможения до остановки:
Полной путь равен s = s1 + s2 = 79 м.
На мокрой дороге или при гололеде величина а может составлять лишь треть величины а на сухой дороге и тормозной путь значительно увеличится.
в) Игрок в бейсбол (рис. 3.15) бросает мяч со скоростью v = 30 м/с (начальная скорость v =0). При броске мяч ускоряется на общем расстоянии (для взрослого мужчины) s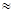 
3,5 м, когда игрок проводит мяч из-за спины до точки, в которой мяч освобождается. Воспользовавшись соотношением (3.7) найдем ускорение, сообщаемое мячу:
Рис. 3.15. Игрок в бейсбол ускоряет мяч на отрезке 3,5 м
Это почти в 13 раз больше ускорения свободного падения.
