Тригонометрические, гиперболические и обратные к ним функции.

Ниже перечислены встроенные в MatLab тригонометрические функции и обратные к ним:

· sin, cos, tan, cot — синус, косинус, тангенс и котангенс;

· sec, csc—секанс, косеканс ();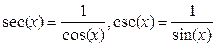

· asin, acos, atan, acot — арксинус, арккосинус, арктангенс и арккотангенс;

· asec, acsc — арксеканс, арккосеканс.

 

Аргументы тригонометрических функций должны быть выражены в радианах. Об­ратные тригонометрические функции возвращают результат также в радианах.

 

В MatLab встроены следующие гиперболические функции и обратные к ним:

· sinh, cosh, tanh, coth — гиперболические синус, косинус, тангенс и котангенс;

· sech, csch — гиперболические секанс и косеканс;

· asinh, acosh, atanh, acoth — гиперболические арксинус, арккосинус, арктангенс и арккотангенс;

· asech, acsch — гиперболические арксеканс и арккосеканс.

 

Экспоненциальная функция, логарифмы, степенные функции.

 

Ниже перечислены примеры этих функций в MatLab:

· ехр — экспоненциальная функция;

· log — натуральный логарифм;

· log10 — десятичный логарифм;

· log2 — логарифм по основанию 2;

· pow2 — возведение числа 2 в степень;

· sqrt — квадратный корень;

· nextpow2 — степень, в которую надо возвести число 2, чтобы получить ближайшее число (большее или равное аргументу).

 

Функции для работы с комплексными числами.

К ним относятся следующие функций MatLab:

· abs, angle — модуль rи фаза φ(в радианах от -π до π ) комплексного числа ;

· complex — конструирует комплексное число по его действительной и мнимой части:

· con j — возвращает комплексно-сопряженное число;

· imag, real — возвращает мнимую и действительную часть комплексного числа.

 

Округление и остаток от деления.

 

Ниже приведены примеры использования этих функций в MatLab:

· fix — округление до ближайшего целого по направлению к нулю;

· floor, ceil — округление до ближайшего целого по направлению к ми­нус бесконечности или плюс бесконечности;

· round — округление до ближайшего целого;

· mod – остаток от целочисленного деления (со знаком);

· rem – остаток от целочисленного деления;

· sign — возвращает знак числа.

 

Использование переменных

 

В MatLab предусмотрена возмож­ность работы с переменными. Причем пользователь не должен заботиться о том, какие значения будет принимать переменная (комплексные, вещест­венные или только целые). Для того чтобы присвоить, например, перемен­ной z значение 1.45, достаточно написать в командной строке z=1.4, при этом MatLab сразу же выведет значение z:

>> z=1.45

z=

1.4500

Здесь знак равенства используется в качестве оператора присваивания. Часто не очень удобно после каждого присваивания получать еще и результат. По­этому в MatLab предусмотрена возможность завершать оператор присваива­ния точкой с запятой для подавления вывода результата в командное окно.

Именем переменной может быть любая последовательность букв и цифр без пробела, начинающаяся с буквы. Строчные и прописные буквы различают­ся, например Mz и mZ являются двумя разными переменными. Количество воспринимаемых MatLab символов в имени переменной составляет 31.

 

Для ввода длинных формул или команд в командную строку следует поставить три точки (подряд, без пробелов), нажать клавишу <Enter> и продолжить набор формулы на следующей строке. Так можно разместить выражение на несколь­ких строках. MatLab вычислит все выражение или выполнит команду после на­жатия на <Enter> в последней строке (в которой нет трех идущих подряд точек).

MatLab запоминает значения всех переменных, определенных во время се­анса работы. Предположим, что часть вычислений с переменными выполнена, а осталь­ные придется доделать во время следующего сеанса работы с MatLab. В этом случае понадобится сохранить переменные, определенные в рабочей среде.

 

Сохранение рабочей среды

 

Самый простой способ сохранить значения всех переменных — использо­вать в меню File пункт Save Workspace As. При этом появляется диалоговое окно Save Workspace Variables, в котором следует указать каталог и имя файла. По умолчанию предлагается сохранить файл в подкаталоге work основного каталога MatLab. Удобно давать файлам имена, содержащие дату работы, например work20-09-01. MatLab сохранит результаты работы в файле work20-11-03.mat. Теперь можно закрыть MatLab одним из следующих способов:

· выбрать в меню File пункт Exit MATLAB;

· нажать клавиши <Ctrl>+<Q>;

· набрать команду Exit в командной строке и нажать <Enter>;

· нажать на кнопку с крестиком в правом верхнем углу окна программы MatLab.

В следующем сеансе работы для восстановления значений переменных сле­дует открыть файл work20-11-03.mat при помощи подпункта Open меню File. Теперь все переменные, определенные в прошлом сеансе, стали доступными. Их можно использо­вать во вновь вводимых командах.

Сохранение и восстановление переменных рабочей среды можно выполнить и из командной строки. Для этого служат команды save и load. В конце сеанса работы с MatLab надо выполнить команду

>> save work20-11-03

Расширение можно не указывать, MatLab сохранит переменные рабочей cреды в файле work20-11-03.mat. В начале следующего сеанса работы для считывания переменных следует ввести команду

>> load work20-01-03

В MatLab имеется возможность записывать исполняемые команды и резуль­таты в текстовый файл (вести журнал работы), который потом можно легко прочитать или распечатать из текстового редактора. Для начала ведения журнала служит команда diary. В качестве аргумента команды diary следу­ет задать имя файла, в котором будет храниться журнал работы. Набираемые далее команды и результаты их исполнения будут записываться в этот файл.

 

Просмотр переменных

При работе с достаточно большим количеством переменных необходимо знать, какие переменные уже использованы, а какие нет. Для этой цели служит команда who, выводящая в командное окно MatLab список исполь­зуемых переменных.

Команда whos позволяет получить более подробную информацию о пере­менных в виде таблицы. Первый столбик таблицы Name состоит из имен используемых переменных. Программа MatLab все данные представляет в виде массивов, в столбике Size указывается размер массива, в котором хранится переменная. В стол­бике Bytes показано, сколько байтов занимает каждая из переменных. В последнем столбике Class указан тип переменных.

Для освобождения из памяти всех переменных используется команда clear. Если в аргументах указать список переменных (через пробел), то только они будут освобождены из памяти.

Начиная с версии 6.0, появилось удобное средство для просмотра переменных рабочей среды — окно Workspace, для перехода к которому следует активизировать одноименную закладку. Данное окно содержит таблицу, аналогичную той, что выводится командой whos.

 

Работа с массивами

Массив — упорядоченная, пронумерованная со­вокупность однородных данных. У массива должно быть имя. Массивы раз­личаются по числу размерностей или измерений: одномерные, двумерные, многомерные. Размером массива называют число элементов, вдоль каждого из измерений. Доступ к элементам осуществляется при помощи индекса. В MatLab нумерация элементов массивов начинается с единицы. Это зна­чит, что индексы должны быть больше или равны единице.

Важно понять, что вектор, вектор-строка, матрица или тензор являются ма­тематическими объектами, а одномерные, двумерные или многомерные мас­сивы — способы хранения этих объектов в компьютере.

Вектор-столбец вводится в командной строке, используя квадратные скобки и разделяя элементы вектора точкой с запятой:

>> a=[1.3; 5.4; 6.9]

a=

1.3000

5.4000

6.9000

Вектор-строка вводится в командной строке, используя квадратные скобки и разделяя элементы вектора пробелом:

>> b=[3 4 9 2]

b =

3 4 9 2

Матрица же вводится следующим образом:

>> c=[ 2 3 3

4 2 3

6 5 6];

Для нахождения суммы векторов используется знак «+», разницы – «-».

Функция sum предназначена для суммирования элементов вектора. Функция sum может быть применена и для матриц sum(имя массива), по умолчанию вычисляется сумма по столбцам, чтобы вычислить сумму по строкам, необходимо вызвать функцию sum с двумя аргументами: sum(имя массива, 2). Заметьте, что sum(имя массива) и sum(имя массива, 1) – идентичные записи.

Перемножение элементов вектора или вектора-строки осуществляется при помощи функции prod. Для матриц функция prod работает аналогично функции sum.

Для нахождения минимума и максимума из элементов вектора служат встроенные функции min и max. По отношению к матрицам функции min и max вычисляют вектор-строку, содержащую минимальные или максимальные элементы в соответствующих столбцах матрицы.

Для нахождения максимума или минимума не по столбцам матрицы, а по строкам предусмотрена следующая форма вызова со вторым аргументом – пустым массивом:

>> max(имя массива, [], 2)

Для того чтобы узнать не только значения максимальных и минимальных элементов, но и их номера, следует вызвать эти функции с двумя выходными аргументами:

>> [m, k]=min(имя массива)

В результате переменной m будет присвоено значение минимального эле­мента массива, а номер минимального элемента занесен в переменную к.

Функция упоря­дочения вектора по возрастанию его элементов - sort. Вызов sort с двумя выходными аргументами приводит к образованию массива индексов соответствия элементов упорядоченного и исходного массивов. Если мы применяем эту функцию для матрицы, то она приводит к упорядочиванию элементов каждого из столбцов матрицы в порядке возрастания. Вызов sort со вторым аргументом, равным двум, приводит к упорядочиванию элементов строк. Так же как и для векторов, функция sort позволяет получить матрицу индексов соответствия элементов исходной и упорядоченной матрицы. Для этого необходимо вызвать sort с двумя выходными аргументами.

Для вычисления определителя матрицы предназначена встроенная функция det. Транспонирование вектора и матрицы производится при помощи .'.

>> B.’

Размерность и размер массива можно узнать при помощи встроенных функций ndis и size.