Лекция 6
Краткое содержание: Поступательное и вращательное движение тела. Простейшие движения твердого тела. Число степеней свободы твердого тела. Поступательное движение твердого тела. Траектория, скорости и ускорения точек тела при поступательном движении. Вращение твердого тела вокруг неподвижной оси, угол поворота, уравнение вращательного движения тела. Угловая скорость и угловое ускорение тела. Скорость и ускорение точки твердого тела, вращающегося вокруг неподвижной оси /скалярные формулы/. Векторные формулы для скоростей и ускорений точек тела.
КИНЕМАТИКА ТВЕРДОГО ТЕЛА
Абсолютно твердым телом называется механическая система, расстояния между любыми двумя точками которой остается постоянным.
Задачи кинематики твердого тела распадаются на две части:
1. задание движения и определение кинематических характеристик движения тела в целом;
2. определение кинематических характеристик (траектория, скорость и ускорение) движения отдельных точек тела.
Существует пять видов движения твердого тела:
поступательное движение; вращение вокруг неподвижной оси; плоское движение;
сферическое движение (вращение вокруг неподвижной точки); свободное движение.
Первые два называются простейшими движениями твердого тела.
Числом степеней свободы твердого тела называется число независимых параметров, которые однозначно определяют положение тела в пространстве относительно рассматриваемой системы отсчета.
Свободная материальная точка в пространстве имеет три степени свободы: например декартовы координаты x, y и z. Материальная точка на плоскости имеет две степени свободы. Если в плоскости выбрать систему координат xОy, то координаты x и y определяют положение точки на плоскости, акоордината z тождественно равна нулю.
Свободная материальная точка на поверхности любого вида имеет две степени свободы. Например: положение точки на поверхности Земли определяется двумя параметрами: широтой и долготой.
Материальная точка на кривой любого вида имеет одну степень свободы. Параметром, определяющим положение точки на кривой, может быть, например, расстояние вдоль кривой от начала отсчета.
Рассмотрим две материальные точки в пространстве, соединенные жестким стержнем длины l. Положение каждой точки определяется тремя параметрами, но на них наложена связь.
Уравнение 
является уравнением связи. Из этого уравнения любая одна координата может быть выражена через остальные пять координат (пять независимых параметров). Поэтому эти две точки имеют (
) пять степеней свободы.
Рассмотрим три материальные точки в пространстве, не лежащие на одной прямой, соединенные тремя жесткими стержнями. Число степеней свободы этих точек равно (
) шести.
Свободное твёрдое тело в общем случае имеет 6 степеней свободы. Действительно, положение тела в пространстве относительно какой-либо системы отсчета, определяется заданием трех его точек, не лежащие на одной прямой, и расстояния между точками в твердом теле остаются неизменными при любых его движениях. Согласно выше сказанному, число степеней свободы должно быть равно шести.
Поступательное движение твердого тела.
Поступательным движением твёрдого тела называется такое его движение, при котором любая прямая, жёстко скреплённая с телом, остаётся параллельной своему первоначальному положению в каждый момент времени.
Теорема. При поступательном движении твёрдого тела траектории, скорости и ускорения всех точек твердого тела одинаковы.
Если выбрать две точки твердого тела А и В, то радиус-векторы этих точек связаны соотношением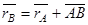 
. Траектория точки А это кривая, которая задается функцией 
, а траектория точки В это кривая, которая задается функцией 
. Траектория точки В получается переносом траектории точки А в пространстве вдоль вектора 
, который не меняет своей величины и направления во времени. Следовательно, траектории всех точек твердого тела одинаковы.
Продифференцируем по времени выражение .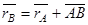
Получаем 
, так как 
. Продифференцируем по времени скорости и получим выражение 
.
Рис. 4-3
Следовательно, скорости и ускорения всех точек твердого тела одинаковы. Что и требовалось доказать.
Поступательное движение твёрдого тела полностью характеризуется движением одной любой его точки.
Твёрдое тело при поступательном движении имеет три степени свободы.
Для задания движения твердого тела в декартовой системе координат достаточно знать координаты любой его точки.
Поэтому уравнения движения любой его точки 
можно назвать уравнениями поступательного движения твердого тела.
