Основы теории упругости
Лекция 4
Плоская задача теории упругости
Слайд 2
В теории упругости имеется большой класс задач, важных в смысле практических приложений и вместе с тем допускающих значительные упрощения математической стороны решения. Упрощение заключается в том, что в этих задачах одну из координатных осей тела, например ось z, можно отбросить и все явления рассматривать происходящими в одной координатной плоскости х0у нагруженного тела. В этом случае напряжения, деформации и перемещения будут являться функциями двух координат – х и у.
Задача, рассматриваемая в двух координатах, называется плоской задачи теории упругости.
Под термином «плоская задача теории упругости» объединяют две физически разные задачи, приводящие к весьма сходным математическим зависимостям:
1) задачу о плоском деформированном состоянии (плоская деформация);
2) задачу о плоском напряжённом состоянии.
Для этих задач чаще всего характерно значительное отличие одного геометрического размера от двух других размеров рассматриваемых тел: большая длина в первом случае и малая толщина во втором случае.
Плоская деформация
Деформация называется плоской, если перемещения всех точек тела могут происходить только в двух направлениях в одной плоскости и не зависят от координаты, нормальной к этой плоскости, т. е.
u=u(x,y); v=v(x,y); w=0 (4.1)
Плоская деформация возникает в длинных призматических или цилиндрических телах с осью, параллельной оси z, вдоль которой по боковой поверхности действует нагрузка, перпендикулярная этой оси и не меняющаяся по величине вдоль неё.
Примером плоской деформации может служить напряжённо-деформированное состояние, возникающее в длинной прямой плотине и длинном своде подземного тоннеля (рис. 4.1).
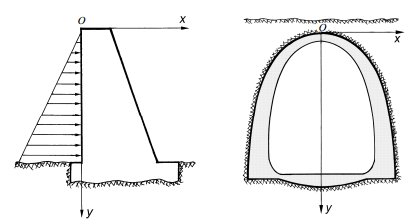
Рисунок – 4.1. Плоская деформация возникает в теле плотины и своде подземного тоннеля
Слайд 3
Подставляя компоненты вектора перемещения (4.1) в формулы Коши (2.14), (2.15), получим:
(4.2)
Отсутствие линейных деформаций в направлении оси z ведёт к появлению нормальных напряжений σz. Из формулы закона Гука (3.2) для деформации εz следует, что
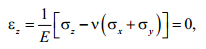
откуда получается выражение для напряжения σz:
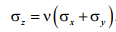(4.3)
Подставляя это соотношение в две первые формулы закона Гука, находим:
(4.4)
Слайд 4
Из анализа формул (4.2) − (4.4) и (3.2) также следует, что
Таким образом, основные уравнения трёхмерной теории упругости в случае плоской деформации значительно упрощаются.
Из трёх дифференциальных уравнений равновесия Навье (2.2) остаются только два уравнения:
(4.5)
а третье обращается в тождество.
Так как на боковой поверхности везде направляющий косинус n=cos(v,z)=cos900=0, Zv=0, то из трёх условий на поверхности (2.4) остаются только два уравнения:
(4.6)
где l, m – направляющие косинусы внешней нормали v к поверхности контура;
X, Y, X v, Y v – компоненты объёмных сил и интенсивности внешних поверхностных нагрузок на оси x и у, соответственно.
Слайд 5
Шесть уравнений Коши (2.14), (2.15) сводятся к трём:
(4.7)
Из шести уравнений неразрывности деформаций Сен-Венана (2.17), (2.18) остаётся одно уравнение:
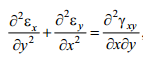(4.8)
а остальные обращаются в тождества.
Из шести формул закона Гука (3.2), с учётом (4.2), (4.4), остаются три формулы:
(4.9)
В этих соотношениях для традиционного в теории упругости вида записи введены новые упругие постоянные:
Слайд 6
Плоское напряжённое состояние
Плоское напряжённое состояние возникает в том случае, когда длина того же призматического тела мала, по сравнению с двумя другими, размерами. В этом случае она называется толщиной. Напряжения в теле действуют только в двух направлениях в координатной плоскости хОу и не зависят от координаты z. Примером такого тела может служить тонкая пластина толщиной h, нагруженная по боковой поверхности (ребру) силами, параллельными плоскости пластины и равномерно распределёнными по её толщине (рис. 4.2).
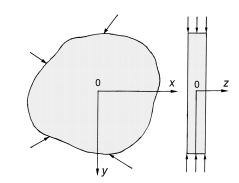
Рисунок 4.2 – Тонкая пластинка и приложенные к ней нагрузки
В этом случае также возможны упрощения, аналогичные упрощениям в задаче о плоской деформации. Компоненты тензора напряжений σz, τxz, τyz на обеих плоскостях пластины равны нулю. Так как пластина тонкая, то можно считать, что они равны нулю и внутри пластины. Тогда напряжённое состояние будет определяться только компонентами σx, σy, τxy которые не зависят от координаты z, т. е. не меняются по толщине пластины, а являются функциями только x и y.
Таким образом, в тонкой пластине возникает следующее напряжённое состояние:
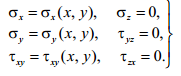
Слайд 7
В отношении напряжений плоское напряжённое состояние отличается от плоской деформации условием
σz=0 (4.10)
Кроме того, из формулы закона Гука (3.2), с учётом (4.10), для линейной деформации εz получаем, что она не равна нулю:
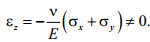
Следовательно, основания пластины будут искривляться, так как появятся перемещения 
по оси z.
При этих предположениях основные уравнения плоской деформации: дифференциальные уравнения равновесия (4.5), условия на поверхности (4.6), уравнения Коши (4.7) и уравнения неразрывности деформаций (4.8) сохраняют такой же вид в задаче о плоском напряжённом состоянии.
Формулы закона Гука примут следующий вид:
(4.11)
Формулы (4.11) отличаются от формул (4.9) закона Гука для плоской деформации только значениями упругих постоянных: E и E1, v и v 1.
Слайд 8
В обратной форме закон Гука запишется так:
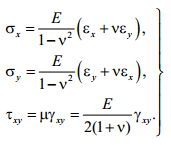(4.12)
Таким образом, при решении этих двух задач (плоская деформация и плоское напряжённое состояние) можно пользоваться одними и теми же уравнениями и объединять задачи в одну плоскую задачу теории упругости.
В плоской задаче теории упругости восемь неизвестных:
– две компоненты вектора перемещений u и v;
– три компоненты тензора напряжений σx, σy, τxy;
– три компоненты тензора деформаций εx, εy, γxy.
Для решения задачи используют восемь уравнений:
– два дифференциальных уравнения равновесия (4.5);
– три уравнения Коши (4.7);
– три формулы закона Гука (4.9), или (4.11).
Кроме того, полученные деформации должны подчиняться уравнению неразрывности деформаций (4.8), а на поверхности тела должны выполняться условия равновесия (4.6) между внутренними напряжениями и интенсивностями внешней поверхностной нагрузки X v, Y v.
