Уравнения состояния реального газа

Тема 6. Реальные газы. Водяной пар. Влажный воздух

Свойства реальных газов

 

Реальные газы отличаются от идеальных тем, что молекулы этих газов имеют объемы и связаны силами взаимодействия, убывающими с ростом расстояния между молекулами. При практических расчетах параметров реальных газов наряду с уравнением состояния применяется отношение

,

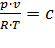называемое коэффициентом сжимаемости.

Для идеальных газов при любых условиях p·v=R·T (уравнение состояния), поэтому для них с =1. Следовательно, коэффициент c выражает отклонение свойств реальных газов от свойств идеальных. Для реальных газов в зависимости от давления и температуры может быть c <1или c >1. При малых давлениях и высоких температурах c ≈1. В этих случаях реальные газы можно рассматривать как идеальные.

Чтобы учесть различие свойств реальных и идеальных газов, нужно иметь уравнения состояния, связывающие величины p, v, T. Поведение реального газа можно описать с высокой точностью с помощью вириального уравнения (уравнения с вириальными коэффициентами):

, (6.1)

где B_v - вириальные коэффициенты, которые выражаются через потенциальную энергию взаимодействия молекул газа и температуру Т.

Уравнение (6.1) в общем виде не может быть использовано для непосредственных расчетов реальных газов. Для отдельных частных случаев получены различные расчетные уравнения. Из-за сложности вычисления вириальных коэффициентов обычно ограничиваются расчетом первых двух коэффициентов. Тогда расчетное уравнение имеет вид:

, (6.2)

где А и В - вириальные коэффициенты, являющиеся функциями только температуры.

 

Уравнения состояния реального газа

 

Наиболее простое уравнение, качественно верно отображающее поведение реального газа, - уравнение Ван-дер-Ваальса:

. (6.3)

В уравнении (6.3) а и b - постоянные величины. Первая учитывает силы взаимодействия, вторая - размер молекул. Отношение a / v ² характеризует добавочное давление, под которым находится реальный газ вследствие сил сцепления между молекулами, называемое внутренним давлением.

Для жидких тел это давление весьма велико (для воды при 20⁰С оно составляет 1050 МПа), а для газов из-за малых сил сцепления молекул - очень мало. Поэтому внешнее давление, действующее на жидкость, оказывает ничтожное влияние на её объем, и жидкость считают несжимаемой. В газах, в виду малости значения a / v ², внешнее давление легко изменяет их объем.

Уравнение Ван-дер-Ваальса качественно верно отображает поведение жидкостей и газов, но для двухфазных состояний оно неприменимо.

На pv -диаграмме (рис.6.1) показаны изотермы, построенные по уравнению Ван-дер-Ваальса. Видно, что при сравнительно низких температурах на кривых имеются волнообразные участки. Чем выше температура, тем короче участки. Этим участкам соответствует непрерывный переход от жидкого состояния к парообразному при данной температуре. Точки А_i отвечают жидкому состоянию, точки В_i - парообразному состоянию вещества.

В действительности переход из жидкого в парообразное состояние всегда происходит через двухфазное состояние вещества (влажный пар). При данной температуре переход происходит при постоянном давлении. Этот действительный переход из жидкого в парообразное состояние изображается прямыми линиями А_iВ_i.

Для особо чистых веществ возможно осуществление участков волнообразной кривой AQ и DB. В первом случае имеют место неустойчивые состояния перегретой жидкости, а во втором - переохлажденного пара.

При определенной температуре изотерма уравнения Ван-дер-Ваальса не будет иметь волнообразного участка (точка К). Точке K соответствует критическая температура. Соединив точки А ₁, А ₂, А ₃… и В ₁, В ₂, В ₃..., получим кривую, похожую на параболу. Кривая АК называется нижней пограничной кривой и соответствует состоянию кипенияжидкости. Кривая КВ называется верхней пограничной кривой и соответствует состоянию сухого насыщенного пара.

Таким образом, для реального вещества pv -диаграмму можно разбить на 3 области:

1 - область жидкого состояния, расположена левее нижней пограничной кривой;

2 - область двухфазных состояний (влажный пар), расположена между нижней и верхней пограничной кривой);

3 - область перегретого пара, расположена правее верхней пограничной кривой и выше критической точки.

Условно область жидкости ограничивают сверху линией КМ - критической изобарой.

Критическую температуру Д. И. Менделеев называл абсолютной температурой кипения, при которой поверхностное натяжение в жидкости становится равным нулю, т.е. исчезает различие между жидкостью и парообразным состоянием вещества (насыщенным паром).

Связь между критическими параметрами и постоянными уравнения Ван-дер-Ваальса:

Т_к =8 а /(27 Rb); p_к=a /(27 b ²); (6.4)

а = (27 R ² Т ² _к)/(64 p_к); b = (27 RТ_к)/(8 p_к). (6.5)

Уравнение Ван-дер-Ваальса при больших плотностях газа дает значительные ошибки. Экспериментально доказано, что коэффициенты а, b сложно зависят от температуры и давления.

М.П. Вукалович и И.И. Новиков в 1939 г. предложили универсальное уравнение состояния реальных газов с учетом ассоциации и диссоциации их молекул:

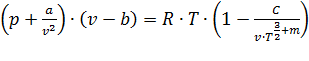, (6.6)

где a, b - постоянные уравнения Ван-дер-Ваальса; С, m - постоянные, определяемые опытным путём.