Раздел 1. Математический анализ
Тема 1.4. Дифференциальные уравнения и их применения в медицине
План
1. Основные понятия и определения дифференциального уравнения.
2. Методы решения некоторых дифференциальных уравнений.
3. Применение дифференциальных уравнений первого порядка для решения задач.
Основные понятия и определения дифференциального уравнения
Опр. Равенство, связывающее независимую переменную х, неизвестную функцию у = f(x), а так же её производные y’,y”,….. yn, называется обыкновенным дифференциальным уравнением.
F(x,y.y’,y”………) = 0, где F – известная функция, заданная в некоторой фиксированной области; х – независимая переменная; у – зависимая переменная; y’,y”,….. yn – её производные.
Опр. Решением дифференциального уравнения называется функция у = f(x), которая будучи представлена в уравнении F(x,y.y’,y”………) = 0, обращает его в тождество. График этой функции называется интегральной кривой.
Пример 1.1. Дифференциальное уравнение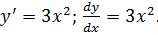 
Представим в виде: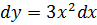 
; возьмём интеграл от левой и правой части уравнения: 
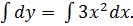Получим 
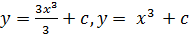– общее решение дифференциального уравнения, которое включает произвольную постоянную с.
Методы решения некоторых дифференциальных уравнений
Выбор метода решения дифференциального уравнения зависит от его вида.
Дифференциальные уравнения первого порядка с разделяющимися переменными.
Уравнения вида 
называется уравнением с разделяющимися переменными, если функция 
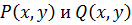разлагаются на множители, зависящие каждый только от одной переменной: 
После резделения переменных, когда каждый член будет зависеть только от одной переменной, общий интеграл уравнения находится почленным интегрированием: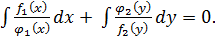 
Решением этого уравнения будет: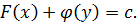 
Пример 2.1. Найти решение уравнения: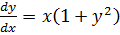 
.
Разделим уравнение на множители, зависящие только от одной переменной: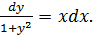 
Проинтегрируем левую и правую части: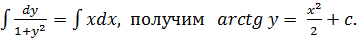 
Общее решение: 
Линейные дифференциальные уравнения первого порядка.
Опр. Уравнения вида: 
, где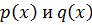 
– непрерывные функции, называются линейными дифференциальными уравнениями первого порядка.
При 
уравнение – называется линейным однородным уравнением.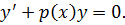 
Общее решение: 
При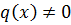 
уравнение – называется линейным неоднородным уравнением. Общее решение: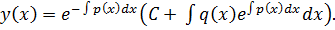 
Применение дифференциальных уравнений первого порядка для решения задач
Этапы решения задач с помощью дифференциальных уравнений:
1. Оформить условия, в которых протекают изучаемые процессы;
2. Выбрать зависимые и независимые переменные;
3. Определить функциональные зависимости между ними
4. Решение уравнения;
5. Анализ полученных решений.
В уравнениях, описывающих медико-биологические процессы, в качестве независимой переменной чаще всего используется временная компонента.
Размножение бактерий
Если бактерии обитают в благоприятной среде, то скорость размножения бактерий пропорциональна размеру популяции. Такое предположение описывается дифференциальным уравнением: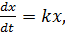 
где х – количество бактерий; k – коэффициент пропорциональности. Тогда, разделяя переменные и интегрируя левую и правую части уравнения 
получим: 
где N0 – начальное количество бактерий; N - количество бактерий в момент времени t.
Вычислим определённые интегралы: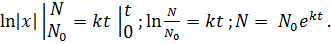 
Получим экспоненциальную кривую, которая зависит от времени и k. Если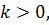 
то количество бактерий будет возрастать по экспоненциальному закону, при 
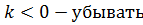, а при 
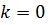- оставаться на постоянном уровне.
| N |
| N0 |
| k<0 |
| k = 0 |
| k>0 |
| t |
Для определения значения k необходимо иметь дополнительные сведения об изменении численности бактерий за определённый промежуток времени.
Внутривенное введение глюкозы
При внутривенном введении с помощью капельницы скорость поступления глюкозы в кровь постоянна и равна с. В крови глюкоза разлагается и удаляется из кровеносной системы со скоростью, пропорциональной имеющемуся количеству глюкозы. Тогда дифференциальное уравнение, описывающее этот процесс, имеет вид: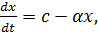 
где х – количество глюкозы в крови в текущий момент времени; с – скорость поступления глюкозы в кровь; 
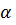- положительная постоянная. Запишем это уравнение в виде: 
Это неоднородное линейное дифференциальное уравнение первого порядка, и его общее решение находиться по формуле: 
где k- постоянная интегрирования. Чтобы найти постоянную k, необходимо знать начальное значение глюкозы в крови х (0).
Тогда 
.
Частное решение уравнения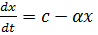 
имеет вид: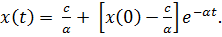 
При увеличении времени уровень глюкозы в крови приближается к 
.
