Контрольная работа №3
ТАБЛИЦА ВАРИАНТОВ К КОНТРОЛЬНОЙ РАБОТЕ № 3
| Номер варианта | Номера задач | |||||
| 3.01 | 3.11 | 3.21 | 3.31 | 3.41 | 3.51 | |
| 3.02 | 3.12 | 3.22 | 3.32 | 3.42 | 3.52 | |
| 3.03 | 3.13 | 3.23 | 3.33 | 3.43 | 3.53 | |
| 3.04 | 3.14 | 3.24 | 3.34 | 3.44 | 3.54 | |
| 3.05 | 3.15 | 3.25 | 3.35 | 3.45 | 3.55 | |
| 3.06 | 3.16 | 3.26 | 3.36 | 3.46 | 3.56 | |
| 3.07 | 3.17 | 3.27 | 3.37 | 3.47 | 3.57 | |
| 3.08 | 3.18 | 3.28 | 3.38 | 3.48 | 3.58 | |
| 3.09 | 3.19 | 3.29 | 3.39 | 3.49 | 3.59 | |
| 3.10 | 3.20 | 3.30 | 3.40 | 3.50 | 3.60 |
ЗАДАЧИ К КОНТРОЛЬНОЙ РАБОТЕ № 3
3.01. Сила тока в цепи изменяется со временем по закону
i =8,5sin(314t + 0,651). Определить амплитудное значение силы тока, его начальную фазу и линейную и циклическую частоту, а также период колебаний. Чему будет равна сила тока в цепи в момент времени t1 = 0,08 с; t2 = 0,042 с? Начертить временную и векторную диаграмму для силы тока.
3.02. Напряжение на катушке изменяется со временем по закону:
u = 60sin (314t + 0,25). Определить амплитудное значение напряжения, его начальную фазу, линейную и циклическую частоту, а также период колебаний. Чему будет равно напряжение на катушке в момент времени t1 = 1,2· 10-2 с? Начертить временную и векторную диаграмму для напряжения.
3.03. Для тела, совершающего свободные колебания, график зависимости смещения от времени представлен на рисунке. Определите период, циклическую и линейную частоту и амплитуду колебаний. Записать уравнение колебаний x(t). Чему будет равно смещение в момент времени t1 = 12· с?
3.04. Колебания материальной точки описываются следующим уравнением: х= 70 sin 0,5 t. Определите амплитуду колебаний, его начальную фазу, линейную и циклическую частоту, период колебаний, а также смещение точки от положения равновесия в следующие моменты времени: 
. Начертить временную и векторную диаграмму для смещения тела.
3.05. Гармоническое колебание описывается уравнением: 
.
Чему равна амплитуда колебаний, циклическая частота колебаний, линейная частота, период, начальная фаза колебаний? Начертить временную и векторную диаграмму для смещения x. Чему будет равно смещение в момент времени t1 = 4· с?
3.06. Сила тока в катушке изменяется со временем по закону: i = 15sin 314t. Определить амплитудное значение силы тока, его начальную фазу и линейную и циклическую частоту, а также период колебаний. Чему будет равны сила тока на катушке в момент времени t1 = 1,2· 10-2 с? Начертить временную и векторную диаграмму для силы тока.
3.07. Колебания материальной точки описываются следующим уравнением:
х= 30sin (3,14t + 1,57). Определите амплитуду колебаний, его начальную фазу, линейную и циклическую частоту, период колебаний, а также смещение точки от положения равновесия в момент времени: t = 0,5·с. Начертить временную и векторную диаграмму для смещения тела.
3.08. Напряжение на конденсаторе изменяется со временем по закону:
u = 20sin (πt + π/4). Определить амплитудное значение напряжения, его начальную фазу, линейную и циклическую частоту, а также период колебаний. Чему будет равно напряжение в момент времени t1 = 0,5 с? Начертить временную и векторную диаграмму для напряжения.
3.09. Скорость колебания материальной точки описываются следующим уравнением: ʋ= 50sin (31,4t). Определите амплитуду колебаний скорости, начальную фазу, линейную и циклическую частоту, период колебаний, а также мгновенную скорость точки в момент времени: t = 0,05· с. Начертить временную и векторную диаграмму для скорости тела.
3.10. Закон колебания ускорения материальной точки описывается следующим уравнением: а= 5sin (πt/4 + π/3). Определите амплитуду колебаний ускорения, его начальную фазу, линейную и циклическую частоту, период колебаний, а также ускорение точки в начальный момент времени. Начертить временную и векторную диаграмму для ускорения тела.
3.11. Точка совершает колебания по закону 
, где A =4 см. Определить начальную фазу, если х(0)=2 см и скорость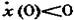 
. Построить векторную диаграмму для момента t =0.
3.12. Точка совершает колебания.по закону 
, где A =4 см. Определить начальную фазу, если x (0)= 
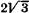см и скорость 
. Построить векторную диаграмму для момента t =0.
3.13. Точка совершает колебания.по закону 
, где A =4 см. Определить начальную фазу, если х (0)= 
см и скорость 
. Построить векторную диаграмму для момента t =0.
3.14. Точка совершает колебания по закону , где A =4 см. Определить начальную фазу, если x (0)= 
см и скорость 
. Построить векторную диаграмму для момента t =0.
3.15. Точка совершает колебания по закону 
, где A =4 см. Определить начальную фазу, если х(0)=2 см и скорость 
. Построить векторную диаграмму для момента t =0.
3.16. Точка совершает колебания по закону , где A =4 см. Определить начальную фазу, если х(0) = 
см и скорость 
. Построить векторную диаграмму для момента t =0.
3.17. Точка совершает колебания по закону 
, где A =4 см. Определить начальную фазу, если х(0)=2см и скорость 
. Построить векторную диаграмму для момента t =0.
3.18. Точка совершает колебания по закону 
, где A =4 см. Определить начальную фазу, если х(0)= 
и скорость 
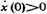. Построить векторную диаграмму для момента t =0.
3.19. Точка совершает колебания по закону 
, где A =4 см. Определить начальную фазу, если 1) х(0)=0 см и скорость 
. Построить векторную диаграмму для момента t =0.
3.20. Точка совершает колебания по закону , где A =4 см. Определить начальную фазу, если 1) х(0)=0 см и скорость 
. Построить векторную диаграмму для момента t =0.
3.21. Колебания материальной точки описываются следующим уравнением:
х= 70 sin 0,5 t. Записать уравнение колебаний скорости и ускорения тела.
3.22. Гармоническое колебание описывается уравнением:
. Записать уравнение колебаний скорости и ускорения тела.
3.23. Колебания материальной точки описываются следующим уравнением:
x = 60sin (314t + 0,25). Записать уравнение колебаний скорости и ускорения тела.
3.24. Колебания материальной точки описываются следующим уравнением:
x =8,5sin(314t + 0,651). Записать уравнение колебаний скорости и ускорения тела.
3.25. Колебания материальной точки описываются следующим уравнением:
x= 15sin 314t. Записать уравнение колебаний скорости и ускорения тела.
3.26. Колебания материальной точки описываются следующим уравнением:
х= 30sin (3,14t + 1,57). Записать уравнение колебаний скорости и ускорения тела.
3.27. Колебания материальной точки описываются следующим уравнением:
x = 20sin (πt + π/4). Записать уравнение колебаний скорости и ускорения тела.
3.28. Колебания материальной точки описываются следующим уравнением:
x= 50sin (31,4t). Записать уравнение колебаний скорости и ускорения тела.
3.29. Закон колебания материальной точки описывается следующим уравнением:
x= 5sin (πt/4 + π/3). Записать уравнение колебаний скорости и ускорения тела.
3.30. Колебания материальной точки описываются следующим уравнением: х= 10 sin (0,5 t – π/4). Записать уравнение колебаний скорости и ускорения тела.
3.31. Два одинаково направленных гармонических колебания одного периода с амплитудами A 1=10 см и A 2=6 см складываются в одно колебание с амплитудой А= 14 см. Найти разность фаз з 
складываемых колебаний.
3.32. Два гармонических колебания, направленных по одной прямой и имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Найти разность фаз з 
складываемых колебаний.
3.33. Определить амплитуду А и начальную фазу результирующего колебания, возникающего при сложении двух колебаний одинаковых направления и периода: 
и 
, где A 1= A 2=1 см; ω=π с-1; τ=0,5 с.
3.34. Точка участвует в двух одинаково направленных колебаниях: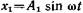 
и 
, где а 1 = 1см; A 2=2 см; ω= 1 с-1. Определить амплитуду А результирующего колебания, его частоту и начальную фазу.
3.35. Складываются два гармонических колебания одного направления с одинаковыми периодами T 1= T 2=1,5 с и амплитудами А 1 =А 2 = 2см. Начальные фазы колебаний 
и 
. Определить амплитуду А и начальную фазу φ результирующего колебания.
3.36. Складываются три гармонических колебания одного направления с одинаковыми периодами Т1=Т2=Т3=2 с и амплитудами A 1= A 2= A 3=3 см. Начальные фазы колебаний φ1=0, φ2=π/3, φ3=2π/3. Построить векторную диаграмму сложения амплитуд. Определить из чертежа амплитуду А и начальную фазу результирующего колебания.
3.37. Складываются два гармонических колебания одинаковой частоты и одинакового направления: 
и x 2= 
. Определить амплитуду А и начальную фазу результирующего колебания. Задачу решить для случая: А 1 = 1см, φ1=π/3; A 2=2 см, φ2=5π/6.
3.38. Складываются два гармонических колебания одинаковой частоты и одинакового направления: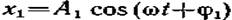 
и x 2= 
. Определить амплитуду А и начальную фазу результирующего колебания. Задачу решить для случая: А1= 1см, φ1=2π/3; A 2=1 см, φ2=7π/6.
3.39. Складываются два гармонических колебания одинаковой частоты и одинакового направления: 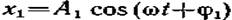и x 2= . Определить амплитуду А и начальную фазу результирующего колебания. Задачу решить для случая: А1= 3см, φ1=π/4; A 2=3 см, φ2=3π/4.
3.40. Складываются два гармонических колебания одинаковой частоты и одинакового направления: 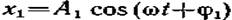и x 2= . Определить амплитуду А и начальную фазу результирующего колебания. Задачу решить для случая: А1= 5см, φ1=π/6; A 2=5 см, φ2=7π/6.
3.41. Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями 
и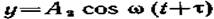 
, где а 1= 2 см, A 2=1 см, 
, τ=0,5 с. Найти уравнение траектории и построить ее, показав направление движения точки.
3.42. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями 
и 
, где а 1 = 4 см, A 1=8 см, 
, τ=1 с. Найти уравнение траектории точки и построить график ее движения.
3.43. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями: 1)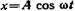 
и 
Принять: А=2 см, A 1=3 см, А 2 = 1см; φ1=π/2, φ2=π. Найти (для первого случая) уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения.
3.44. Решить задачу № 3.43 для второго случая.
3.45. Решить задачу № 3.43 для третьего случая.
3.46. Решить задачу № 3.43 для четвертого случая.
3.47. Решить задачу № 3.43 для пятого случая.
3.48. Решить задачу № 3.43 для шестого случая.
3.49. Решить задачу № 3.43 для седьмого случая.
3.50. Решить задачу № 3.43 для восьмого случая.
3.51 К источнику переменного напряжения и = 300sin 200πt подключены последовательно катушка индуктивностью L = 0,5 Гн, конденсатор емкостью С = 10 мкФ, активное сопротивление R = 100 Ом. Определить амплитудное значение силы тока, сдвиг фаз между током и напряжением. Начертить временную и векторную диаграмму для напряжения.
3.52. Цепь, находящаяся под напряжением U = 120 В, состоит из последовательно соединенных активного сопротивления R = 6 Ом и реактивных XL = Хс =10 Ом. Найти силу тока в цепи и напряжение на каждом сопротивлении.
3.53. Найти сдвиг фаз между силой тока и напряжением для цепи, состоящей из последовательно включенных резистора сопротивлением R = 1 кОм, катушки индуктивностью L = 0,5 Гн и конденсатора емкостью С = 1 мкФ. Найти мощность, выделяемую в цепи, если амплитуда напряжения Um = 100 В, а частота тока v = 50 Гц.
3.54. В цепь переменного тока с частотой v = 50 Гц и напряжением U = 220 В включены последовательно конденсатор, активное сопротивление R = 100 Ом и катушка индуктивностью L = 0,7 Гн. Определить емкость конденсатора, если сила тока в цепи I = 1,34 А.
3.55 В цепи (рис.) R = 20 Ом, L = 0,2 Гн, С = 100 мкФ, эффективное напряжение U = 75 В и частота v = 50 Гц. Найти эффективную силу тока и разность фаз между напряжением и током. Определить эффективное напряжение на каждом участке цепи.
3.56. К источнику переменного напряжения и = 100sin (200πt+π) подключены последовательно катушка индуктивностью L = 50 мГн, конденсатор емкостью С = 40 мкФ, активное сопротивление R = 200 Ом. Определить амплитудное значение силы тока, сдвиг фаз между током и напряжением, и потребляемую мощность.
3.57. В сеть переменного тока с эффективным напряжением U = 110 В и частотой v = 100 Гц последовательно включены конденсатор емкостью С = 5∙10-5 Ф, катушка индуктивностью L = 0,2 Гн и омическое сопротивление R = 4 Ом. Определить: а) эффективную силу тока в цепи; б) частоту тока, при которой в данном контуре наступит резонанс напряжений.
3.58. При включении катушки в цепь постоянного тока с напряжением U1 = 12 В амперметр показал силу тока I1 = 4 А. При включении той же катушки в цепь переменного тока с частотой v = 50 Гц и напряжением U2 = 12 В амперметр показал I2 = 2,4 А. Определить индуктивность катушки. Нарисовать векторную диаграмму.
3.59. В цепь переменного тока частотой v = 50 Гц последовательно включены резистор R = 628 Ом и катушка индуктивности. При этом между колебаниями напряжения и силы тока наблюдается сдвиг фазы на φ = 
. Какова индуктивность катушки? Какую емкость нужно включить в цепь, чтобы сдвиг фазы между силой тока и напряжением стал равен нулю?
3.60. В цепь переменного тока с частотой v = 50 Гц и напряжением U = 220 В включены последовательно конденсатор, активное сопротивление R = 100 Ом и катушка индуктивностью L = 0,7 Гн. Рассчитать емкость конденсатора, при которой возникает резонанс напряжений. Определить силу тока в цепи при резонансе. Зарисовать для этого случая векторную диаграмму.
